Грампластинка и дифракция света (А. Бондарь)

Как известно, один из самых точных методов определения спектрального состава исследуемого излучения основан на явлении дифракции. Хорошим спектральным аппаратом является дифракционная решетка. Оказывается, обычную грампластинку тоже можно использовать для наблюдения дифракции и, в частности, для измерения длины волны видимого света.

Во время звукозаписи на поверхность пластинки на равных расстояниях друг от друга наносятся бороздки. Эти бороздки рассеивают свет, а промежутки между ними отражают его. Таким образом, грампластинка подобна отражательной дифракционной решетке. Если ширина отражающих полос равна a, а ширина рассеивающих бороздок - b, то величина d = a + b является периодом решетки.

Пусть на отражательную решетку с периодом d падает плоская монохроматическая волна длины λ под углом θ к решетке. Согласно принципу Гюйгенса - Френеля, каждая точка отражающей поверхности решетки становится самостоятельным точечным источником, посылающим свет по всевозможным направлениям. Рассмотрим волны, распространяющиеся под углом φ к решетке (см. рис. 122). С помощью собирающей линзы (например, хрусталика глаза) эти волны можно собрать в одну точку. Найдем условие, когда при сложении волны будут усиливать друг друга.

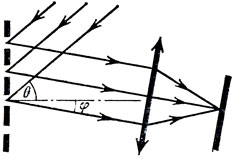
Рис. 122

Разность хода лучей 1 и 2, идущих от соответствующих точек А и В двух соседних отражающих участков решетки (рис. 123), равна

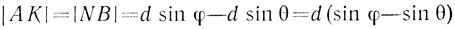
(KB - фронт отраженной волны в направлении под углом φ, AN - фронт падающей волны). Если разность хода кратна длине волны, фазы колебаний, пришедших из точек А и В, будут одинаковыми,.и поэтому колебания будут усиливать друг друга. Аналогично ведут себя и все остальные отражающие участки решетки. Следовательно, условие образования главных максимумов можно записать так:

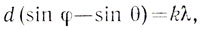
(1)

где k = 0, 1, 2, ... . Отсюда можно определить длину волны λ. Для этого надо знать период решетки d, угол θ падения волны на решетку и направление на соответствующий максимум - угол φ. Обычно период решетки много больше длины волны (d>>λ), поэтому углы φ малы. Это означает, что главные максимумы располагаются очень близко друг к другу и дифракционная картина получается очень нечеткой. Однако чем больше угол падения лучей на решетку (угол θ), тем больше углы и, следовательно, тем удобнее производить необходимые измерения. Вот почему лучше использовать не нормальное, а наклонное падение лучей на решетку.

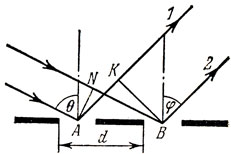
Рис. 123

До сих пор мы говорили о монохроматическом свете. А если на решетку падает белый свет, сложный по своему спектральному составу? Из уравнения (1) непосредственно следует, что положение каждого главного максимума зависит от длины волны. Чем меньше длина волны, тем меньшему значению угла φ соответствует максимум. Таким образом, все максимумы (кроме нулевого) растягиваются в спектр, фиолетовый конец которого обращен к центру дифракционной картины, а красный - наружу. По обе стороны от центрального (нулевого) максимума расположены два спектра первого порядка, затем два спектра второго порядка и т. д. По мере увеличения порядка спектра расстояние между соответствующими линиями спектров увеличивается, так что спектры могут накладываться друг на друга. Например, для солнечного света спектры второго и третьего порядков уже частично перекрываются.

Теперь перейдем непосредственно к опыту. Чтобы измерить длину волны, соответствующую определенному цвету, надо определить период решетки (d), синус угла падения света на решетку (sin θ) и синус угла, определяющего направление на какой-нибудь максимум, например, на максимум первого порядка (sin φ₁). Период решетки легко найти, проигрывая пластинку:

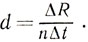
Здесь ΔR - абсолютная величина перемещения иглы вдоль радиуса пластинки за время Δt, n - число оборотов в единицу времени. Обычно d≈0,01 см.

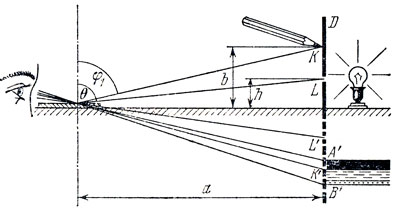
Рис. 124

В качестве источника света можно использовать обычную настольную лампу. Чтобы свет от нее не мешал наблюдению дифракционной картины, сделайте из картона экран со щелью и прикройте им лампу. При этом нить накала лампы должна быть видна через щель. Установите лампу около одной стены комнаты, пластинку положите горизонтально около противоположной стены и найдите изображение щели (рис. 124). Одновременно вы увидите размытые цветные полосы. Это и есть спектр первого порядка (k = 1). Легко проверить, что действительно, чем больше угол θ, тем шире получается цветное изображение щели и тем точнее можно измерить угол, под которым дифрагирует свет интересующей нас длины волны.

Для определения sin φ₁ надо попросить товарища подержать карандаш (или какой-нибудь другой предмет) над щелью так, чтобы его изображение в отраженном от решетки (как от плоского зеркала) свете совпало с выбранным участком спектра (см. рис. 124). Измерив линейкой a, b и h, найдем sin φ₁ и sin θ:

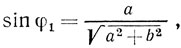
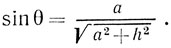
Эти выражения можно несколько упростить. Поскольку b<a и h<<a,

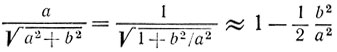
и

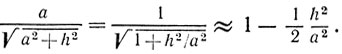
Тогда окончательно

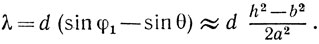
Измерив длины волн света различных цветов, интересно сравнить их с табличными значениями. В наших опытах при тщательных измерениях ошибка была порядка 10^-8 м. Для длин волн видимого света (λ~10^-7м) такая точность вполне допустима.