Шарик вместо линзы (Г. Косоуров)

В основе геометрической оптики лежит представление о прямолинейности световых лучей. Этому учит нас практика. Вы сами можете легко провести опыт, подтверждающий прямолинейность распространения света. Замените объектив фотоаппарата листком черной бумаги, в котором проколото маленькое отверстие. Такой "дырочной камерой" (ее называют камерой-обскурой) можно получать фотографии ярко освещенных предметов, подобно фотографии, приведенной на рис. 125. Эта фотография получена камерой "Зенит", у которой объектив был заменен листком черной бумаги с отверстием диаметром 0,22 мм. Чувствительность пленки 65 ед. ГОСТ, выдержка 5 с. Изображение на пленке точно соответствует центральной проекции точек предмета прямыми, проходящими через отверстие, что является веским аргументом в пользу представления о лучах света как о прямых линиях.

Рис. 125

Образование тени на белом экране от непрозрачного предмета мы объясняем как проекцию контура предмета на плоскость экрана лучами, выходящими из каждой точки источника света. Так как источник света обычно имеет довольно большие размеры, граница тени окружена полутенью и размыта. Можно было бы думать, что, уменьшая размеры источника, мы будем сужать область полутени и в пределе получим резкую тень. Однако опыт показывает совсем другое. Когда источник света становится достаточно мал, обнаруживаются явления; которые раньше маскировались полутенью. Прямой край непрозрачной пластинки вместо резкой тени дает картину, приведенную на рис. 126. Тень снята на расстоянии 0,5 м, от экрана в белом свете через красный светофильтр. Снимок увеличен. Расстояние между двумя первыми темными полосами равно 0,6 мм. Край тени размыт, а параллельно ему идут темные и светлые полосы уменьшающейся контрастности. Если источник света белый, то полосы окрашены в радужные цвета.

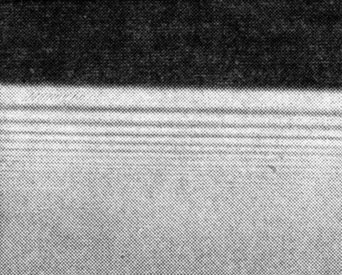
Рис. 126

Тень от тонкой проволоки (рис. 127) также имеет сложную структуру. Снаружи она окаймлена полосами, как у края непрозрачной пластинки, а внутри тени видны темные и светлые полосы, тем более узкие, чем толще проволока. (Этот снимок сделан в белом цвете через красный светофильтр. Диаметр проволоки 12 мм расстояние от проволоки до пленки 0,5 м.)

Рис. 127

Совсем неожиданно выглядит тень от шарика или от маленького непрозрачного диска (рис. 128). Кроме темных и светлых колец, окружающих тень и аналогичных уже знакомым нам полосам, в центре тени можно видеть яркое светлое пятно, как будто бы в центре диска проколото маленькое отверстие. (Для этого снимка был взят шарик диаметром 2,5 мм, использовался красный светофильтр; R₁ = R₂ = 0,5 м.)

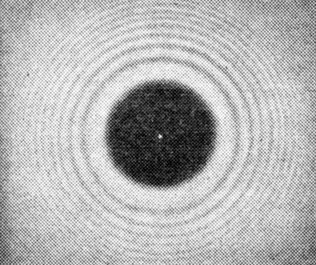
Рис. 128

Явления, в которых обнаруживается, что свет распространяется не строго по законам геометрической оптики, называются дифракционными. Причина их возникновения лежит в волновой природе света Точное описание распространения света дает не построение лучей, а картина распространения волн.

Представим себе круговые волны, расходящиеся от брошенного камня по спокойной поверхности пруда. Если волны достигают плавающего на поверхности бревна, то за бревном образуется вполне четкая тень границы которой определяются лучами, проведенными из точки падения камня через концы бревна. Однако в области тени тоже можно заметить волнение поверхности воды, хотя и более слабое. Это и есть дифракция которая в данном случае не очень искажает картину геометрической тени. Если же волны встретят на своем пути сваю, то уже на небольшом расстоянии за ней картина распространения волн будет мало походить на геометрическую тень. Наконец, если волны встретят торчащий из воды тонкий шест, то тень вообще не образуется. Волны свободно огибают малые препятствия На поверхности воды можно будет заметить лишь слабую круговую волну, рассеянную шестом.

Таким образом, при распространении волн могут встретиться как случаи, когда прямолинейные лучи хорошо описывают наблюдаемые явления, так и случаи когда преобладает дифракционная картина Все зависит от соотношения между длиной волны, размерами препятствия (или отверстия), ограничивающего волну и расстоянием до плоскости наблюдения. Коротко это можно сформулировать так: если из точек экрана на котором мы наблюдаем тень, препятствие или отверстие видно под углом большим, чем угол, под которым видна длина волны с расстояния, равного поперечнику препятствия, то дифракция не сильно искажает лучевую картину. В виде формулы это можно записать так: 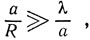где а - размер отверстия, R - расстояние до экрана, на котором наблюдается тень, и λ - длина волны. Если же углы сравнимы или первый угол меньше второго, т. е. 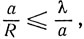то дифракция играет определяющую роль и лучевые представления неприменимы.

В оптике чаще всего имеют дело с первым случаем, так как длины волн видимого света очень малы (от 0,7 мкм для красного света до 0,4 мкм для фиолетового), но на больших расстояниях от маленького отверстия или от тонкой проволоки может быть и второй случай.

Наблюдать явления дифракции света можно с помощью весьма скромных средств. Проколите в тонкой фольге кончиком острой иголки отверстие 0,1-0,2 мм и наклейте фольгу на лист картона с отверстием, который нужен для того, чтобы свет от источника - обычной настольной лампы - не мешал наблюдениям. Установив лист картона на подставке, спроектируйте на него линзой с фокусным расстоянием 4-6 см увеличенное изображение волоска лампы так, чтобы часть изображения волоска пришлась на отверстие в фольге. За отверстием образуется световой конус, который легко найти по светлому кружку на матовом стекле или глазом (когда глаз попадает в световой конус, отверстие кажется ярко светящимся). На расстоянии около 0,5 м от отверстия в пучок света будем помещать объекты, а дифракционную картину будем наблюдать на расстоянии тоже около 0,5 м за объектом. Вести наблюдение следует через слабую лупу или линзу с фокусным расстоянием 2-5 см, укрепив ее на подставке, а глаз располагать на таком расстоянии от линзы, чтобы она вся казалась ярко освещенной. На светлом фоне хорошо будет видна дифракционная картина.

Рис. 129

На рис. 129 приведена фотография установки, на которой получены все помещенные в этой статье дифракционные картины. Была использована оптическая скамья, что, конечно, не обязательно, однако если вам удастся воспользоваться для укрепления объектов какими-либо штативами с винтовыми перемещениями, то приводить дифракционную картину в центр поля зрения будет значительно легче. Цифрами на рисунке обозначены: 1 - лампа; 2 - проектирующая линза; 3 - точечная диафрагма со светозащитным экраном; 4 - держатель с объектами дифракции; 5 - светозащитная труба; 6 - фотоаппарат без объектива.

Тень от прямолинейного края непрозрачного экрана вам даст лезвие безопасной бритвы. Из двух лезвий можно сделать щель шириной 0,3-1 мм. Кусочек проволоки диаметром до 1 мм продемонстрирует дифракцию от узкого экрана. Интересно выглядит дифракция от кончика иголки.

Для наблюдения светлого пятна в центре тени от круглого предмета возьмите стальной шарик от подшипника диаметром 2-4 мм. Капелькой клея приклейте шарик к стеклянной пластинке. (Необходимо следить за тем, чтобы клей не выступал за контур шарика, а поверхности стекла и шарика были чистыми.) Когда клей подсохнет, укрепите пластинку с шариком на остановке. Перемещая пластинку, приведите тень от шарика в центр поля зрения. При этом будут хорошо видны и внешние дифракционные кольца, и пятно в центре, окруженное темными и светлыми кольцами.

Вы, вероятно, захотите получить фотографии дифракционных картин. Это легко сделать, если воспользоваться фотоаппаратом с вывинченным объективом. Тень от объекта проектируется прямо на плоскость пленки. Чтобы дифракционные полосы на фотографии были более четкими и число их было больше, отверстие, служащее источником света, надо закрыть светофильтром, лучше красным, так как в спектре лампы накаливания много красных лучей. Для обычных пленок экспозиция в 5-10 с оказывается достаточной. Чтобы избежать засветки пленки, между аппаратом и объектом нужно поместить зачерненную внутри трубу.

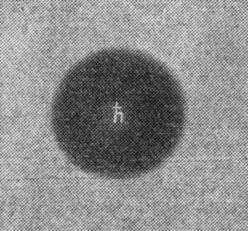
Рис. 130

Смещение источника света вызывает смещение тени, а значит, и пятна. Поэтому, если вместо точечного источника вы возьмете диапозитив малого размера, то каждая прозрачная точка на нем даст свою, слегка смещенную тень шарика со своим светлым пятном. В результате внешние дифракционные кольца размажутся, а в центре тени можно будет увидеть изображение диапозитива. Шарик будет действовать как линза. Именно так была получена фотография символа постоянной Планка (рис. 130). Фотография получена с помощью шарика диаметром 4 мм. Высота символа ћ равна 1 мм. Диапозитив был получен фотографированием на контрастной пленке буквы, вычерченной тушью на бумаге.

Просверлив в тонкой жести круглое отверстие диаметром около 2 мм, вы сможете проследить, как меняется дифракционная картина от круглого отверстия на разных расстояниях от него. Закрыв источник света светофильтром и приближая глаз с лупой к отверстию, начиная с расстояний 1-2 м, вы увидите, как в центре картины появляются черные кружки, которые при приближении глаза превращаются в темные кольца, расходящиеся к краям тени. Число темных колец, считая и темное пятно в центре, определяется разностью путей света для центрального луча и луча, идущего от края отверстия. Этим можно воспользоваться для определения длины волны света. Чтобы произвести вычисления, необходимо знать диаметр отверстия, измерить расстояние от источника света до отверстия и расстояние от отверстия до плоскости наблюдения. Определить положение плоскости наблюдения можно, поместив в поле зрения лупы иголку и двигая ее до тех пор, пока она не будет представляться глазу резкой на фоне изучаемой дифракционной картины. Как вывести расчетную формулу, мы поясним ниже.

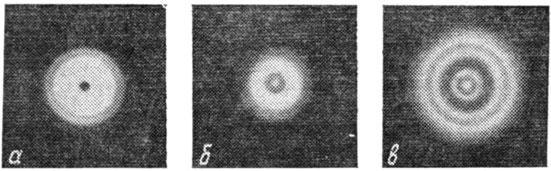
Рис. 131

В белом свете можно наблюдать красивую смену окраски дифракционных колец. Цвета, которые вы увидите, не похожи на спектральные. Они называются дополнительными и наблюдаются тогда, когда из полного спектра белого света удаляется какая-нибудь одна спектральная область. В нашем случае, когда, например, в центре получается темное пятно для зеленого света, остальные части спектра, то есть красно-оранжевый и фиолетовый, окрашивают центр картины в пурпурный цвет. Отсутствие красного приводит к зелено-голубому дополнительному цвету и т. д. На рис. 131 приведены примеры дифракционных картин от круглого отверстия: а) диаметр отверстия 1 мм, R₁ = R₂ = 0,5 м. Красный светофильтр. Отверстие открывает две зоны. В центре черное пятно, б) То же с (синим светофильтром. Отверстие открывает почти три зоны, в) Диаметр отверстия 1,5 мм, R₁ = R₂ = 0,5 м. Красный светофильтр. Отверстие открывает немногим более четырех зон.

Почему же в центре, куда волны приходят, казалось бы, беспрепятственно, появляется темное пятно?

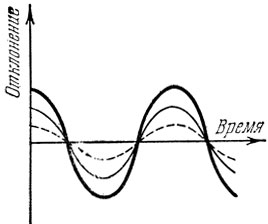
Рис. 132

Вернемся к нашим наблюдениям волн на поверхности пруда. Представим себе, что одновременно в пруд бросили два камня и по его поверхности распространяются две системы волн. Тогда на поверхности пруда найдутся точки, в которые одновременно приходят горбы от обеих систем волн. Через некоторое время в эти же точки одновременно придут впадины волн. Волны будут усиливать друг друга, как это показано на рис. 132. Усиление будет происходить, в точках, лежащих на разных расстояниях от источников волн. Кроме того, волны будут усиливаться в тех точках, расстояния от которых до источников волн отличаются на целую длину волны, на две длины волны и т. д. В тех точках, до которых одновременно доходят горбы от одной волны и впадины от другой, волны будут ослабляться, гасить друг друга, как это показано на рис. 133. Описанное явление называется интерференцией. Оно играет решающую роль в образовании дифракционных картин.

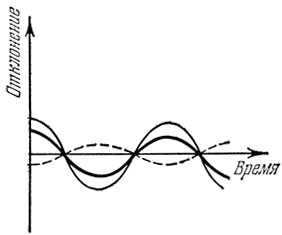
Рис. 133

Каждая точка пространства, через которую проходит световая волна, сама может рассматриваться как источник вторичной сферической волны (рис. 134). Если свет проходит через круглое отверстие, то мы можем заменить источник света вторичными источниками, распределенными по площади отверстия. Все эти источники будут колебаться в такт с первичной волной, дошедшей до отверстия. Амплитуда колебаний в точке наблюдения за экраном найдется как сумма колебаний, которые вызывает в этой точке каждый вторичный источник. Нужно учесть, что волны от разных источников проходят разные пути и, складываясь, могут не только взаимно усиливаться, но и ослабляться.

Рис. 134

Проследим, как будет меняться амплитуда колебаний на оси круглого отверстия, освещенного точечным источником света. Когда расстояние до точки наблюдения очень велико по сравнению с диаметром отверстия, волны от всех вторичных источников проходят почти одинаковые пути и, приходя в точку наблюдения, взаимно усиливаются. При приближении точки наблюдения к отверстию вторичные волны от источников, расположенных на краю отверстия, будут заметно отставать от волн, пришедших от источников центральной зоны, и результирующая амплитуда будет уменьшаться. Когда луч, проведенный в точку наблюдения от края отверстия, станет длиннее луча, проведенного из центра, на целую длину волны, наступит полная компенсация колебаний, и в центре дифракционной картины мы увидим темное пятно. Еще приблизив экран, мы нарушим компенсацию колебаний на оси, и центр дифракционной картины снова станет светлым. Теперь возникнет компенсация на некотором расстоянии от оси, и центр дифракционной картины будет окружен темным кольцом. Когда крайний луч отстанет от центрального на две длины волны, снова наступит компенсация колебаний на оси. Дифракционная картина будет иметь вид светлого пятна с темным центром и с одним темным кольцом.

Появление темного пятна в центре дифракционной картины будет периодически повторяться по мере приближения экрана, на котором наблюдается дифракционная картина, к экрану с отверстием. Сосчитав число темных колец, можно сказать, сколько раз произошла компенсация на оси. То же самое можно увидеть, если менять не расстояние до точки наблюдения, а радиус отверстия. Этих указаний достаточно для того, чтобы вы сами вывели формулу для определения длины волны. Итак, желаем успеха!