Переговорная трубка длиной в экватор?

А уши у стен и в самом деле были. 
Вернее, одно ухо: круглая дырка, 
от которой шла труба - нечто 
вроде секретного телефона, 
передававшего все, что 
говорилось в подземелье, 
прямехонько в комнату 
кавалера Помидора.

Дж. Родари. "Приключения Чиполлино"

Сравнительно недавно, около сорока лет назад, ученые СССР и США обнаружили удивительное явление. Распространяющиеся в океане звуковые волны иногда удавалось зарегистрировать за тысячи километров от их источника. Так, в одном из наиболее удачных экспериментов звук от подводного взрыва, произведенного учеными у берегов Австралии, обошел половину земного шара и был зарегистрирован другой группой исследователей у Бермудских островов на расстоянии 19600 км от Австралии (рекорд дальности распространения импульсных звуковых сигналов). Каков же механизм такого, сверхдальнего, распространения звука?

Для того чтобы ответить на этот вопрос, вспомним, что со случаями неожиданно далекого распространения звуков приходится сталкиваться не только между берегами Австралии и Бермудским треугольником, но и в повседневной жизни. Так, сидя на кухне за завтраком, часто можно услышать не слишком приятное дребезжание, которое какой-то шутник назвал "пением водопроводных труб". Прекратить это "коммунальное музицирование" иногда удается, открыв водопроводный кран в своей квартире^*. Большинство людей после этого облегченно возвращаются к прерванному завтраку, не особенно задумываясь над физической сущностью происшедшего явления. А задуматься стоит. Почему звук, возбуждаемый струей воды в неисправном кране в одной из квартир, не дает покоя обитателям всего подъезда, связанного одним водопроводным стояком? Ведь если в той же квартире свистнуть в свисток, то это услышат разве что соседи в ближайших квартирах. "Пение" же водопроводных труб слышно везде, с первого до последнего этажа.

^* (О причинах "пения" водопроводных труб см. статьи Е. М. Воинова и Е. И. Пальчикова (Квант, 1984, № 7).)

Такое различие обусловлено двумя причинами. Первая- это звукоизолирующее действие стен и перекрытий, которые отражают и поглощают звуки свистка. А звуковая волна, распространяющаяся по водопроводной трубе, проходит с этажа на этаж беспрепятственно. Теперь о второй причине. При звучании свистка возникающая акустическая волна распространяется в пространстве по всем направлениям, и ее волновой фронт имеет форму сферы. Площадь этой сферы растет по мере удаления от источника звука, и интенсивность звуковой волны - то есть энергия, проходящая через единицу площади волнового фронта в единицу времени,- по мере удаления от источника падает (найдите сами, по какому закону). А звуковая волна, возникающая внутри водопроводной трубы, "одномерна": отражаясь от стенок трубы, она не расходится во все стороны в пространстве, а распространяется в одном направлении - вдоль самой трубы - без расширения волнового фронта; так что интенсивность звука по мере удаления от источника практически не изменяется. В этом смысле водопроводная труба представляет собой акустический волновод - канал, в котором звуковые волны распространяются практически без ослабления.

Другой пример акустического волновода - переговорные трубы, с помощью которых с давних времен и по сей день на судах передаются команды с капитанского мостика в машинное отделение. Заметим, что затухание звука в воздухе при распространении по волноводу оказывается настолько малым, что если бы удалось сделать такую трубку длиной в 700 км, то она смогла бы служить своеобразным "телефоном" для передачи разговора, например, из Москвы в Ленинград и обратно. Однако вести разговор по такому телефону было бы крайне затруднительно, поскольку собеседник слышал бы сказанное вами примерно через полчаса.

Подчеркнем, что отражение распространяющейся в волноводе волны от его границ является определяющим свойством волновода - именно благодаря ему энергия волны распространяется не во все стороны в пространстве, а передается в заданном направлении.

Приведенные примеры наводят на мысль, что и сверхдальнее распространение звука в океане, с которого мы начали этот раздел, обусловлено волноводным механизмом. Однако как же образуется такой гигантский волновод? При каких условиях он может возникнуть и что в этом случае служит его отражающими границами, заставляющими звуковые волны распространяться на столь огромные расстояния?

В качестве верхней границы может служить поверхность океана, которая достаточно хорошо отражает звук. Соотношение между интенсивностями отраженной и прошедшей сквозь границу раздела двух сред звуковой волны существенно зависит от плотностей этих сред и значений скоростей звука в каждой из них. Если среды различаются сильно (например, для воды и воздуха плотности отличаются почти в тысячу раз, а скорости звука в 4,5 раза), то даже при нормальном (перпендикулярно к поверхности) падении звуковой волны на плоскую границу раздела между водой и воздухом практически вся волна отразится обратно в воду - интенсивность прошедшей в воздух звуковой волны составит всего лишь 0,01 % падающей. При наклонном падении волна отражается еще сильнее. Однако поверхность океана редко бывает ровной из-за постоянного волнения; а это приводит к хаотическому рассеянию на ней звуковых волн и, таким образом, к нарушению волноводного характера их распространения.

Не лучше обстоит дело и с отражением от дна океана. Плотность донных осадков обычно лежит в пределах 1,24-2,0 ^г/_см³, а скорость распространения звука в них всего на 2-3 % меньше, чем в воде. Поэтому, в отличие от границы "вода - воздух", значительная доля энергии падающей из воды на дно звуковой волны поглощается в донном грунте.

Таким образом, дно отражает звук слабо, и служить нижней границей волновода никак не может.

Итак, границы волновода в океане следовало искать где-то между дном и поверхностью. И они были найдены. Этими границами оказались слои воды на определенных глубинах океана.

Как же происходит отражение звуковых волн от "стенок" подводного звукового канала (ПЗК)? Чтобы ответить на этот вопрос, нам придется рассмотреть, как вообще происходит распространение звука в океане.

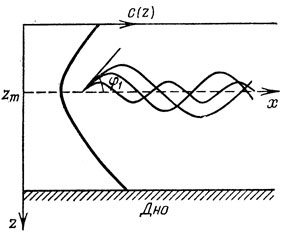
Рис. 1

До сих пор мы говорили о волноводах, молчаливо предполагая, что скорость распространения звука в них постоянна. Между тем известно, что скорость звука в океане колеблется от 1450 до 1540 ^м/_с. Она связана с температурой воды, ее соленостью, с величиной гидростатического давления и с другими факторами. Рост гидростатического давления приводит к тому, что при погружении на каждые 100 м скорость звука увеличивается примерно на 1,6 ^м/_с. С ростом температуры скорость звука также возрастает. Однако в океане температура воды, как правило, довольно резко убывает по мере удаления из верхних, хорошо прогретых слоев воды в глубину, где она выходит практически на постоянное значение. Действие этих двух механизмов приводит к такой зависимости скорости звука от глубины, как это показано на рис. 1. Вблизи поверхности преобладающее влияние оказывает быстрое падение температуры - в этих слоях скорость звука уменьшается с ростом глубины. По мере погружения температура меняется медленнее, а гидростатическое давление продолжает возрастать. На некоторой глубине влияние этих двух факторов "уравновешивается" - здесь скорость звука оказывается минимальной; а дальше она начинает возрастать с увеличением глубины за счет роста гидростатического давления.

Итак, скорость распространения звука в океане зависит от глубины. И это сказывается на характере распространения звука. Для того чтобы понять, чем определяется ход звуковых лучей в океане, мы обратимся к оптической аналогии: посмотрим, как распространяется световой луч в стопке из плоскопараллельных пластинок с различными показателями преломления, а затем обобщим наш результат на случай среды с плавно меняющимся показателем преломления.

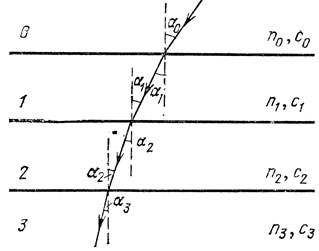
Рис. 2

Рассмотрим стопку из плоскопараллельных пластин с разными показателями преломления n₀, n₁,..., n_k,..., причем n₀<n₁<...<n_k<... (рис. 2). Луч, падающий из самой верхней пластинки на пластинку 1 под углом α₀, после преломления на границе 0-1 составит угол α₁ с нормалью к этой границе; под таким углом он упадет на границу 1-2; после преломления на этой границе луч, пройдя пластину 2, упадет на границу 2-3 под углом α₂, вновь преломится и т. д. Согласно закону преломления

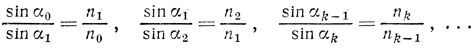
Вспоминая, что отношение коэффициентов преломления двух сред обратно отношению скоростей распространения света в этих средах, перепишем все соотношения в виде

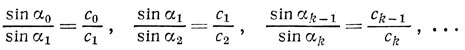
(c₀>c₁>...>c_k>...). Перемножив последовательно эти равенства друг на друга, получим соотношение

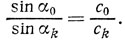
Устремляя толщину каждой пластинки к нулю, а число пластинок к бесконечности, мы придем к обобщенному закону преломления, который описывает ход светового луча в среде с плавно меняющимся показателем преломления (этот закон называют обобщенным законом Снеллиуса):

где с(0) - скорость света в месте входа луча в среду, с (z) - скорость света на расстоянии z от границы среды. При таком предельном переходе ломаная линия, показывающая ход луча, превращается в плавную кривую. Таким образом, при распространении светового луча в оптически неоднородной среде по мере увеличения скорости света (уменьшения показателя преломления) этот луч все больше отклоняется от вертикали и "прижимается" к границе раздела.

Явление искривления световых лучей при распространении света в среде с непрерывно меняющимся показателем преломления называют рефракцией.

Зная, как меняется скорость света в среде, мы можем, пользуясь обобщенным законом Снеллиуса, указать, каким будет ход того или иного луча, попавшего в неоднородную среду. Точно так же происходит искривление и звуковых лучей при распространении z, звука в неоднородной среде, где изменяется скорость звука. Частный случай такой среды и представляет собой океан.

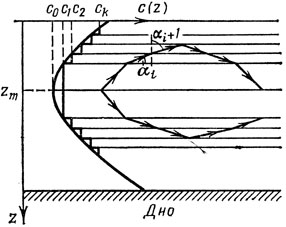
Рис. 3

Теперь вернемся к вопросу о том, как распространяется - звук в ПЗК. Представим себе, что источник звука находится на глубине z_m, соответствующей минимуму скорости звука (рис. 3). Каков будет ход звуковых лучей, выходящих из источника? Луч, идущий вдоль горизонтали z = z_m, будет прямолинейным. А те лучи, которые выходят под некоторым углом к этой горизонтали, будут искривляться. По аналогии это явление называют рефракцией звука. Поскольку и выше, и ниже уровня z_m скорость звука возрастает, звуковые лучи будут искривляться в направлении горизонтали z = z_m; в какой-то момент луч станет "параллельным" этой горизонтали и, "отразившись", повернет к ней (см. рис. 3).

Итак, рефракция звука в океане приводит к тому, что часть звуковой энергии, излучаемой источником, может распространяться, не выходя на поверхность воды и не доходя до дна. А это и означает, что в такой среде реализуется волноводный механизм распространения звука - подводный звуковой канал. Роль "стенок" этого волновода выполняют слои воды на тех глубинах, где происходит "поворот" звукового луча.

Уровень глубины z_m, на которой скорость звука минимальна, называют осью ПЗК. Обычно величины z_m лежат в диапазоне 1000-1200 м; однако в тропических широтах, где вода прогревается на большую глубину, ось ПЗК может опускаться и до глубин в 2000 м. Наоборот, в высоких широтах влияние температуры на распределение скорости звука сказывается только в приповерхностном слое, и ось ПЗК поднимается до глубин 200-500 м, а в полярных широтах - еще ближе к поверхности.

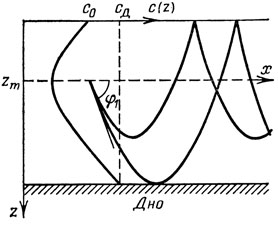
Рис. 4

В океане могут существовать два различных типа ПЗК. Канал первого типа образуется в том случае, когда скорость звука у поверхности воды (с₀) меньше, чем у дна (с_д). Этот случай обычно имеет место в глубоководных районах, где давление у дна достигает сотен атмосфер. Как мы уже говорили, звук, идущий из воды в воздух, хорошо отражается от поверхности их раздела, и если поверхность океана гладкая (штиль), то она служит резкой верхней границей волновода, и канал занимает весь слой воды от поверхности до дна (рис. 4).

Посмотрим, какая часть звуковых лучей "захватывается" в ПЗК. Для этого перепишем соотношение Снеллиуса в таком виде:

где φ₁ и φ (z) - углы, образуемые звуковым лучом с горизонтальной плоскостью на глубинах z₁ и z соответственно. Эти углы называют углами скольжения (понятно, что φ₁ = ^π/₂ - α₁, φ(z) = ^π/₂ - α(z)). Если источник звука находится на оси ПЗК, то c₁ = c_m; канал захватывает лучи, для которых угол скольжения у дна равен φ(z) = 0. Так что все лучи, которые выходят из источника под углами скольжения φ₁, удовлетворяющими условию (см. рис. 4)

попадают в ПЗК.

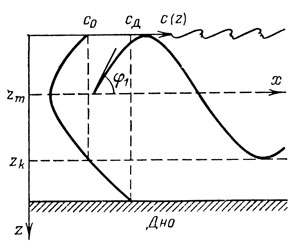
Рис. 5

При неровной поверхности воды звуковые лучи будут рассеиваться на ней; те лучи, которые уйдут от поверхности под достаточно большими углами скольжения, дойдут до дна и там поглотятся. Однако и в этом случае канал может захватывать все те лучи, которые благодаря рефракции чуть-чуть не доходят до волнующейся поверхности (рис. 5). Канал при этом простирается от поверхности до глубины z_k, которая определяется из условия c(z_k) = c₀. Понятно, что такой канал захватывает все звуковые лучи с углами скольжения

Канал второго типа характерен для мелководных районов и образуется в случае, когда скорость звука вблизи поверхности оказывается большей, чем у дна (рис. 6). Он занимает слой воды от дна до глубины z_k, такой, что c(z_k) = c_д. Это как бы перевернутый канал первого типа в случае волнующейся поверхности.

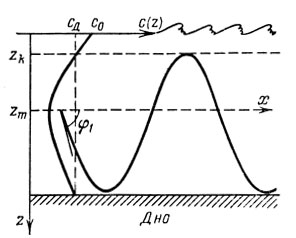
Рис. 6

Если источник звука расположен вблизи оси ПЗК, то в точку приема сигнала приходит, как правило, множество звуковых лучей, причем время прохождения звука по ним различно и оказывается максимальным для осевого луча (скорость распространения звука на этой глубине минимальна). Интенсивность короткого импульсного сигнала, регистрируемого в точке приема, растет от начала приема к концу, поскольку разность между временами прихода импульсов по разным лучам к концу приема сигнала уменьшается, и они начинают накладываться один на другой, что и приводит к увеличению интенсивности. Последним приходит звуковой луч, распространяющийся вдоль оси ПЗК (с нулевым углом скольжения), после чего сигнал резко обрывается.

Для определенных типов зависимости скорости звука от глубины ПЗК действует на звуковые лучи подобно фокусирующей линзе: если излучатель расположен на оси ПЗК, то лучи, вышедшие под различными углами скольжения, будут периодически одновременно сходиться на оси канала в точках, называемых фокусами ПЗК. Так, для канала, в котором скорость звука меняется с глубиной по закону, близкому к параболическому - с (z) = с_ь ( 1 + ¹/₂b²z²), фокусы для лучей, вышедших под малыми углами скольжения, будут находиться в точках x_n = x₀ + ^πn/_b, где n = 1, 2,..., а b - некоторый коэффициент, имеющий размерность, обратную длине (рис. 7). Такой профиль кривой c(z) близок к реальному распределению скорости звука в глубинных ПЗК. Отклонения от точной параболической зависимости в с (z) приводят к размытию фокусов на оси ПЗК.

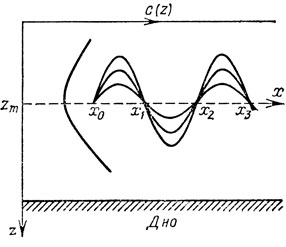
Рис. 7

Ну, а можно ли заставить звук, распространяющийся по ПЗК, совершить кругосветное путешествие - обогнуть под водой весь земной шар и вернуться к своему источнику? Нет, нельзя. Первой и самой непреодолимой преградой служат материки и значительные перепады в глубинах Мирового океана. Поэтому нельзя выбрать такой путь, вдоль которого существовал бы единый ПЗК, вокруг всего земного шара. Но это не единственная причина. Звуковая волна, распространяющаяся в ПЗК, отличается от звуковых волн в водопроводной трубе и переговорной трубке. Как уже говорилось, при распространении в этих волноводах звуковая волна одномерна, площадь ее волнового фронта постоянна на любом расстоянии от источника звука, и следовательно, интенсивность звука (без учета тепловых потерь) также будет постоянна в любом сечении трубы. В подводном звуковом канале звуковая волна распространяется не вдоль прямой, а по всем направлениям в плоскости z = z_m. Поэтому волновым фронтом является цилиндрическая поверхность, и уже из-за этого интенсивность звука падает по мере удаления от источника пропорционально 1/R, где R - расстояние от источника звука до места наблюдения (получите эту зависимость и сравните ее с полученным вами ранее законом убывания интенсивности для сферической звуковой волны в трехмерном пространстве),

Другой причиной ослабления звука служит затухание звуковой волны при ее распространении в морской воде. Энергия волны переходит в тепло из-за вязкости воды, а также других необратимых процессов. Кроме того, звуковая волна рассеивается в океане на различных неоднородностях, которыми могут служить взвешенные в воде частицы, пузырьки воздуха, планктон и даже газовые пузыри рыб.

В заключение заметим, что описанный подводный звуковой канал - отнюдь не единственный пример волновода, существующего в природе. Так, дальнее радиовещание с наземных радиостанций возможно только благодаря распространению радиоволн в атмосфере по гигантским волноводам. В определенных условиях в атмосфере могут образовываться волноводные каналы и для электромагнитных волн светового диапазона. Тогда, в результате сверхдальних миражей, в центре пустыни можно увидеть величаво плывущий морской корабль, а среди океана вдруг поднимается город.