В голубом просторе

Когда же солнце вас расплавит, 
Серебряные облака, 
И будет вышина мягка, 
И крылья тишина расправит?

О. Мандельштам

Острой профессиональной наблюдательностью отличаются художники, поэтому мир, отраженный художниками-реалистами в их пейзажах, особенно ярок и многокрасочен, а отдельные явления природы проступают явственнее. И при этом даже очень хорошему художнику нет нужды понимать подчас весьма сложную сущность происходящих в природе явлений, которые он реалистически отображает на своих полотнах. Но вот изучать окружающий мир по картинам хорошего художника-пейзажиста можно даже лучше, чем в натуре, ибо в пейзаже автор как бы останавливает мгновенье, интуитивно усиливая существенное и опуская лишнее, случайное.

Всмотритесь в картину Аркадия Александровича Рылова "В голубом просторе", репродукция ее приведена на второй странице обложки. "Белые птицы, как и облака, легко парят, купаясь в голубой лазури. И так же плавно, как белая птица, по спокойно колышущимся синим волнам океана скользит покрытый парусами корабль",- так описывает эту картину известный искусствовед А. А. Федоров-Давыдов. Любуясь в Третьяковской галерее этим замечательным полотном, забываешь, что стоишь в зале музея, и ощущаешь себя участником этого праздника природы.

А теперь отвлечемся от живописи и посмотрим на картину глазами исследователя. Прежде всего, откуда художник писал пейзаж - со скалистого уступа берега или с борта корабля?

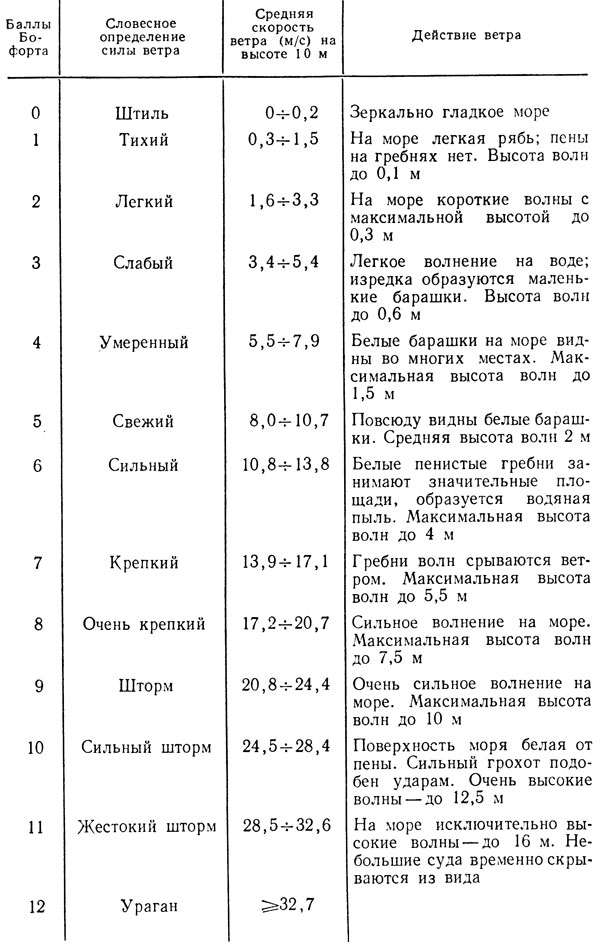
Шкала Бофорта

Скорее всего, он был на корабле, так как на переднем плане картины не видно прибоя, распределение волн симметрично и не искажено близким присутствием берега.

Давайте попытаемся оценить скорость ветра, который раздувает паруса корабля, скользящего вдали. Мы не первые, кто задается вопросом оценки скорости ветра по величине волн или по другим проявлениям в окружающей нас природе. Еще в 1806 г. английский адмирал Ф. Бофорт разработал двенадцатибалльную шкалу для приближенной оценки скорости ветра по его действию на наземные предметы и по волнению в открытом море. Эта шкала принята Всемирной метеорологической организацией, ею пользуются и поныне.

Взглянув на картину, видим, что волнение на воде легкое, изредка на гребнях волн образуются маленькие белые барашки. Это, согласно шкале Бофорта, соответствует слабому ветру со скоростью около 5 ^м/_с.

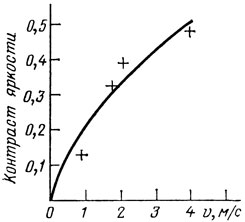
Заметим, что о скорости ветра можно судить не только по шкале Бофорта, но и по контрасту яркости неба и моря. При наблюдении горизонта в открытом море, как правило, видна четкая граница между небом и морем. Только при полном штиле их яркости становятся одинаковыми. Контраст в этом случае исчезает, море и небо сливаются воедино. Такое явление в природе наблюдается довольно редко - штиль для этого должен быть практически абсолютным - 0 баллов по шкале Бофорта. При малейшем ветре на поверхности моря появляются волны. Коэффициент отражения света от наклонных участков поверхности уже не равен единице - поэтому и возникает контраст между яркостью неба и моря, который может быть измерен экспериментально. Так, зависимость контраста яркостей моря и неба от скорости ветра была измерена во время одной из экспедиций научно-исследовательского судна "Дмитрий Менделеев". На приведенном рисунке крестиками показаны результаты измерений, сплошной линией - найденная А. В. Бялко и В. Н. Пелевиным теоретическая зависимость.

А кстати, почему барашки белые и так сильно отличаются по цвету от сине-зеленого моря?

Цвет моря определяется многими факторами, среди которых важнейшими являются положение солнца, цвет неба, рельеф поверхности моря, глубина моря; если глубина невелика, то важным фактором является наличие или отсутствие в воде водорослей и содержание в ней взвешенных твердых частиц. Все эти факторы влияют на отражение света от поверхности моря, на поглощение и рассеяние света в глубине. Поэтому однозначное объяснение видимого цвета моря просто невозможно. Но кое в чем разобраться можно. Так, например, можно понять, почему цвет ближайших к художнику волн гораздо темнее общего фона моря, а к горизонту море становится светлее.

Степень отражения световой волны при падении на границу раздела двух сред с разными оптическими плотностями определяется углом падения а и относительным показателем преломления сред. Количественно ее характеризуют коэффициентом отражения, который равен отношению интенсивностей отраженного и падающего света^*. Коэффициент отражения зависит от угла падения. Чтобы обнаружить эту зависимость, понаблюдайте, как отражаются лучи дневного света от поверхности полированного стола. Здесь оптически более плотной средой служит прозрачный слой лака. Вы увидите, что при скользящих лучах отражается практически весь световой поток, а с уменьшением угла падения все большая часть светового потока проникает в среду с большей оптической плотностью и все меньшая часть отражается от поверхности раздела. Коэффициент отражения убывает с уменьшением угла падения.

^* (Интенсивностью света называют среднее (по времени) значение светового потока через единицу поверхности площадки, перпендикулярной к направлению распространения света.)

Обратимся теперь к схематическому изображению волны, показанному на рис. 1 (см. вторую стр. обложки), из которого видно, что углы падения α₁ и α₂ лучей, попа-дающих в глаз наблюдателя от "фронта" волны и от "спины", разные и α₂>α₁" Поэтому от удаленных областей моря в глаз наблюдателя попадает больше отраженного света, и передний фронт волны виден более темным, чем ровная поверхность моря сзади. В случае многих волн на поверхности моря угол а, вообще говоря, меняется в зависимости от того, смотрим ли мы на гребень волны или на впадину вблизи или вдалеке от фронта волны. Однако с удалением от переднего фронта угловой размер темных гребней быстро уменьшается, а угол α₂ все равно остается большим угла α₁. По мере удаления к горизонту картина волн как бы усредняется, наблюдатель уже не видит долин между волнами, и постепенно темные склоны волн исчезают совсем. Поэтому на картине область моря вблизи горизонта кажется более светлой, чем на переднем плане.

Теперь мы можем объяснить, почему барашки на гребнях волн белые. Бурлящая вода в барашках содержит множество пузырьков воздуха, которые непрерывно движутся, лопаются, меняют форму. Углы отражения меняются от точки к точке и во времени. Поэтому в пене барашка солнечные лучи почти полностью отражаются, и барашки воспринимаются белыми.

На цвет моря в большой степени влияет цвет неба над ним. И если первый, как мы уже говорили, предсказать практически невозможно, то цвет неба можно понять на основании физических законов. Ясно, что цвет неба определяется рассеянием солнечных лучей в земной атмосфере. Но почему рассеяние лучей солнца, спектр которого сплошной, то есть содержит все длины волн, приводит к синему, голубому цвету неба, а само солнце мы видим желтым? Разобраться в этом вопросе нам поможет закон Релея для рассеяния света.

В 1898 г. английский физик Релей создал теорию рассеяния света на частицах, размеры которых значительно меньше длины волны рассеиваемого света. Найденный им закон гласит: интенсивность рассеянного света пропорциональна четвертой степени частоты световой волны, или обратно пропорциональна четвертой степени длины волны. Для объяснения цвета неба Релей применил свой закон к рассеянию солнечного света в атмосфере (поэтому иногда сформулированный выше закон называют "законом синего неба").

Попробуем понять качественно содержание закона Релея. Свет представляет собой электромагнитные волны. Молекулы состоят из ядер и электронов - частиц заряженных. Попадая в поле электромагнитной волны, эти заряженные частицы начинают двигаться, причем можно считать, что их движение происходит по гармоническому закону: x(t) = A₀ sin ωt, где A₀ - амплитуда колебаний, а ω - частота световой волны. При таком движении заряженные частицы обладают ускорением a = x"_t = A₀ω² sinωt. Однако ускоренно движущиеся заряженные частицы сами становятся источниками электромагнитного излучения - так называемых вторичных волн. Амплитуда такой вторичной волны пропорциональна ускорению порождающей ее частицы (равномерно движущиеся заряженные частицы, как известно, создают электрический ток, но не излучают электромагнитных волн). Соответственно интенсивность излучения вторичных волн оказывается пропорциональной квадрату ускорения движения электронов в поле первичной волны (движением тяжелых ядер можно пренебречь), а следовательно, четвертой степени частоты (l~а²~(x_t")²~ω₄).

Но вернемся к цвету неба. Отношение длины волны красного к длине волны синего света равно 650 нм/450 нм = 1,44 (1 нм (нанометр) = 10^-9 м). Возводя это число в четвертую степень, получим 4,3. Таким образом, согласно закону Релея интенсивность рассеянного в атмосфере синего света в четыре раза превышает интенсивность рассеянного красного света, и слой воздуха толщиной в десятки километров приобретает окраску с заметным преобладанием синих и голубых цветов. А видимый солнечный свет, который дошел до нас сквозь "заслон" атмосферы, в большей степени лишен коротковолновой части своего спектра. Поэтому солнце, которое мы видим в прошедших сквозь атмосферу лучах, принимает слабый желтый оттенок. Этот o оттенок может усиливаться, становиться оранжевее и краснее по мере захода солнца, когда солнечным лучам приходится преодолевать больший путь в атмосфере (при восходе солнца, естественно, смена цветов происходит в обратном порядке).

Заметим, что в законе Релея предполагается только, что длина волны рассеиваемого света намного превышает размеры рассеивающих частиц, однако сам этот размер в выражение для интенсивности не входит. Релей первоначально предполагал, что цвет неба обусловлен рассеянием солнечного света на мельчайших частицах, запыляющих атмосферу. Однако позже он пришел к убеждению, что солнечные лучи рассеиваются на молекулах газов, входящих в состав воздуха. Через десять лет, в 1908 г., польский физик-теоретик М. Смолуховский высказал идею о том, что рассеивателями в оптически однородной среде должны выступать весьма неожиданные объекты - неоднородности плотности частиц. С помощью этой гипотезы Смолуховскому удалось объяснить известное задолго до его исследований явление критической опалесценции - сильного рассеяния света в жидкости или газе вблизи критической точки. Наконец, А. Эйнштейн в 1910 г. создал последовательную количественную теорию молекулярного рассеяния света, основанную на идее Смолуховского. Для газов интенсивность рассеянного света, вычисленная по формуле Эйнштейна, в точности совпала с результатом, полученным ранее Релеем.

Все, казалось бы, стало на свои места. Но откуда берутся неоднородности в плотности воздуха? Ведь он находится в состоянии термодинамического равновесия, а если даже дует ветер, то связанные с этим движением неоднородности имеют гигантские размеры, превышающие длину волны света в огромное число раз, и на рассеянии света сказываться никак не могут.

Для понимания природы неоднородностей показателя преломления света давайте более детально разберемся с понятием термодинамического равновесия. Для простоты рассмотрим некоторый макроскопический объем газа, находящийся в замкнутом сосуде.

Физика рассматривает системы, состоящие из гигантского числа частиц, поэтому единственно возможный путь описания свойств таких систем - статистический. Статистический подход означает, что мы следим не за состоянием каждой молекулы в отдельности, а вычисляем средние значения соответствующих физических величин для всей системы в целом. При этом вовсе не обязательно, чтобы для всех молекул значение рассматриваемой физической величины равнялось соответствующему среднему. При рассмотрении нашего макроскопического объема газа наиболее вероятным будет состояние, в котором молекулы газа распределены в среднем равномерно по всему объему сосуда. Однако благодаря тепловому движению молекул всегда имеется отличная от нуля вероятность того, что концентрация молекул в некоторой области сосуда на некоторое время превысит среднюю концентрацию молекул в рассматриваемом объеме (при этом, естественно, в другой области рассматриваемого объема концентрация молекул на это время понизится). Теоретически возможно даже такое состояние, когда все молекулы газа соберутся в одной половине объема рассматриваемого сосуда, а вторая окажется абсолютно пустой. Но вероятность такого события выражается столь малым числом, что нет никакой надежды на его реализацию даже в пределах существования Вселенной, которое по современным представлениям составляет 1010 лет.

Однако небольшие отклонения физических величин от их средних значений возможны, и не только возможны, но и постоянно происходят благодаря тепловому движению молекул. Эти отклонения называются флуктуациями (от латинского слова fluctuari - колебаться). Именно они и приводят к тому, что в некоторых областях плотность газа возрастает, а в других убывает, что сказывается на величине коэффициента преломления света в данных областях.

Если мы теперь вернемся к рассмотрению рассеяния света в атмосфере, то все рассуждения, проведенные для ограниченного объема газа, останутся справедливыми. Кроме того, так как воздух является смесью различных газов, различие в тепловом движении молекул разных газов приводит к дополнительным возможностям появления неоднородностей коэффициента преломления света в пространстве, обусловленных флуктуациями.

Характерный размер неоднородности коэффициента преломления света (неоднородности плотности) зависит от температуры. Для слоев атмосферы, в которых происходит основное рассеяние солнечного света, размеры таких неоднородностей оказываются много меньшими длины волны видимого света, но значительно превышающими размеры молекул газов, входящих в состав воздуха. Поэтому рассеяние света происходит именно на них, а не на молекулах, как это предполагал Релей.

И все же небо мы видим синим, а не фиолетовым, хотя закон Релея предсказывает преобладание фиолетового цвета. Оказывается, что это расхождение обусловлено двумя причинами. Во-первых, в спектре солнечного света гораздо меньше фиолетовых лучей, чем синих. Вторым виновником кажущегося расхождения теории и практики является наш "регистрирующий прибор" - глаз человека с нормальным зрением. Дело в том, что острота зрительного восприятия человеческого глаза существенно зависит от длины волны света. На рис. 2 (см. вторую стр. обложки) приведена экспериментально построенная кривая, характеризующая эту зависимость. Из рисунка видно, что на фиолетовые лучи глаз реагирует гораздо слабее, чем на сине-зеленые. Именно поэтому воспринимаемые человеческим глазом рассеянные солнечные лучи практически не имеют фиолетовой компоненты.

А почему же на голубом небе мы ясно видим белые облака? Разве при рассеянии света на составляющих их частицах не справедливы выводы из закона Релея?

Дело в том, что облака состоят из мельчайших капель воды или кристалликов льда, размеры которых, однако, значительно превышают длины волн видимого света. По-этому при рассеянии солнечного света на частицах, составляющих облака, закон Радея не применим - рассеяние света всех длин волн в этом случае происходит приблизительно с одинаковой интенсивностью, и облака воспринимаются белыми, что мы и видим на картине.

Всмотритесь теперь в форму облаков. По картине видно, что хотя верхняя часть облака рыхлая и клубящаяся (эти облака и называют кучевыми), нижняя граница резко очерчена. С чем это связано? Оказывается, что кучевые облака (в отличие от слоистых) образуются при конвекционном подъеме от поверхности земли теплых, насыщенных влагой слоев воздуха. По мере подъема над морем (как и над сушей) температура воздуха падает. Понятно, что для высот над уровнем моря, много меньших радиуса Земли и расстояния до ближайшего берега, поверхности постоянной температуры (изотермы) близки к плоскостям, параллельным поверхности моря. При этом вблизи поверхности моря падение температуры происходит достаточно быстро - примерно один градус на сотню метров (вообще говоря, зависимость температуры воздуха от высоты далеко не линейна, однако до высот в несколько километров приведенные цифры верны).

Но вернемся к поднимающемуся потоку воздуха. Как только он достигает высоты, температура воздуха на которой соответствует точке росы для содержащегося в нем водяного пара, пар начинает конденсироваться в мельчайшие капельки воды. Этой изотермой и определяется нижняя граница облака. Учитывая, что размеры облака по горизонтали составляют сотни и тысячи метров, мы видим, что предлагаемое объяснение приводит к достаточно четко очерченной нижней границе облака, так как конденсация водяного пара будет происходить с разбросом в несколько десятков метров по высоте, что гораздо меньше горизонтального размера облака. В подтверждение сказанного на заднем плане картины мы видим целый ряд облаков с плоскими нижними границами, которые висят на одном уровне над морем.

Но поднимающийся воздух после образования нижней границы облака не останавливается, а, быстро охлаждаясь, продолжает подниматься вверх. Оставшиеся в нем водяные пары интенсивно конденсируются и вот уже начинают превращаться не в капельки воды, а в кристаллики льда, из которых обычно и состоит верхняя граница кучевого облака. Потеряв всю влагу и охладившись, воздух останавливается и начинает свое обратное движение вниз. Он растекается в стороны и опускается, обтекая облако. Из-за описанных конвекционных потоков и образуются характерные барашки на верхней границе кучевых облаков, а из-за того, что охладившийся воздух опускается вниз, эти облака, как правило, не образуют непрерывную массу, а разделены чистыми промежутками голубого неба.

На переднем плане картины клином летит стая белых птиц. Оценим частоту взмахов крыльев птицы средних размеров (массой m ≈ 10 кг, с площадью крыла S ≈ 1 м²) в условиях полета без планирования. Пусть средняя скорость движения крыла 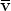. Тогда за время Δt при движении крыла вниз птица сообщит массе воздуха Δm = ρS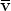Δt (ρ - плотность воздуха) скорость 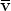, то есть передает ей импульс Δ 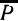= ρS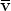

²Δt. Для того чтобы птица держалась на заданной высоте, этот импульс должен компенсировать соответствующее воздействие силы тяжести: Δ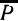 = mgΔt. Отсюда находим, что

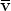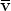mg = ρS ²

и, таким образом, для средней скорости движения крыла имеем 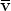= √mg/ρS. Эту скорость уже можно связать с частотой v взмахов крыльями и длиной крыла L соотношением

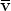= ωL = 2πvL.

Считая, что L∼√S, находим

Итак, согласно нашей оценке птица должна делать примерно один взмах в секунду, что по порядку величины вполне разумно.

Интересно исследовать полученную формулу подробнее. Сделаем грубое предположение, что у всех птиц, независимо от размеров и пород, форма тела одинакова. Тогда площадь крыла можно связать с массой птицы соотношением S~m^2/₃. Подставляя это в найденное нами выражение для частоты взмахов крыльями, находим, что

Таким образом, мы видим, что с уменьшением размеров птицы частота ее взмахов крыльями возрастает, в чем легко убедиться на опыте. Конечно, сделанное нами предположение о единстве формы всех птиц очень грубое - у больших птиц крылья даже относительно гораздо больше, чем у малых, однако этот факт только усиливает найденную нами тенденцию.

Заметим, что ту же формулу (*) (однако без существенного множителя 2π) можно было легко получить просто методом размерностей. Действительно, ясно, что частота взмахов зависит только от веса птицы, площади ее крыльев S и плотности окружающего воздуха ρ. Записывая v = ρ^αS^β (mg)^γ и сравнивая размерности физических величин в левой и правой частях этого равенства, находим, что α = -γ = -¹/₂, β = -1.

Мы далеко не исчерпали всех тех вопросов и ответов, которые можно найти в "Голубом просторе". Пытливому и наблюдательному зрителю в этой картине могут открыться и другие, может быть, более интересные явления. Да и нет надобности ограничиваться картиной - интересные вопросы и задачи можно найти везде в окружающем нас повседневном мире.