Лунные дорожки

А в воде - в реке, в пруде, в озерах, в яме 
Фонарями разбросалася луна.

И. Северянин. "Nocturne"

Отражения самых различных источников света от поверхности воды часто имеют вид длинных дорожек света, направленных от источника к нашему глазу. Вспомните хотя бы отражение солнца в море во время заката или отражения от уличных фонарей набережной в реке. Широкую полосу света отбрасывает луна, отражаясь в море или озере.

Все эти явления происходят вследствие того, что каждая маленькая волна на поверхности воды дает свое отдельное изображение. Попробуем разобраться, почему все освещенные волны вместе образуют продолговатую фигуру, вытянутую от источника света к наблюдателю,- дорожку.

Мы уже говорили, что рябь образуется на воде при волнении 1-3 балла по шкале Бофорта. При меньшем ветре поверхность воды отражает как плоское зеркало (состояние штиля). При большем она покрывается белыми барашками, и световая дорожка теряет резкие очертания. Рябь можно представить как множество мелких волн, разбросанных по поверхности воды абсолютно неправильно и возникающих одинаково часто во всех направлениях. Крутизна склона волн при этом не превышает некоторого предельного значения α, которое зависит от силы ветра и может достигать 20-30°.

Попробуем теперь найти границу полосы света, несколько упростив задачу. Именно, будем считать, что в каждом месте поверхности имеется большое число маленьких зеркальных волн, крутизна склонов которых меняется в пределах от 0 до α, и волны имеют различные направлениям. Кроме того, для простоты будем считать, что наблюдателя и источник света находятся на одном уровне над поверхностью воды h (рис. 1).

Маленькое горизонтальное зеркальце будет отбрасывать свет в глаз наблюдателя 0 только в том случае, когда расстояния от него до наблюдателя и до источника одинаковы (в точке М). Если же зеркало наклонено под углом а в сторону наблюдателя, то для того чтобы отраженный свет! попадал в глаз, оно должно быть несколько сдвинуто от наблюдателя (точка N). Зеркальце, наклоненное под углом! а в противоположную сторону, должно находиться в точке N'.

Наклонные положения зеркала аналогичны крайним положениям волн, при которых отраженный от них свет еще попадает в наш глаз. Поэтому расстояние между N и N' определяет длину световой дорожки. Во всех точках между N к N' найдутся участки волн, имеющие достаточный наклон для того, чтобы отражать лучи в наш глаз.

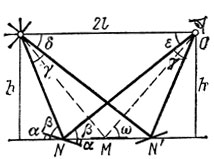
Рис. 1

Рассмотрим теперь углы между лучами света. Из рис. 1 видно, что β + α = γ + δ, β - α = ε = δ, откуда γ = α + β - (β - α) = 2α. Таким образом, мы приходим к выводу, что угол, под которым мы видим большую ось светового пятна, просто равен углу между двумя наиболее крутыми склонами. Нетрудно посчитать и линейный размер большой ось пятна NN'.

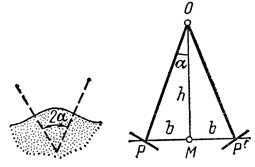
Рис. 2

Короткая ось пятна отраженного света легко находится аналогичным способом. Если сместить зеркальце из точки М в направлении, перпендикулярном NN', то для того чтобы отраженный свет попал в глаз наблюдателя, зеркальце надо повернуть на некоторый угол вокруг оси, параллельной NN' (рис. 2). Считая, что предельный угол поворота зеркальца по-прежнему равен а, находим, что ширина полосы света pp' = 2h tgα, и следовательно, короткая ось стягивает угол β = ^2htgα/_√(t²+h²)

Отношение двух видимых полуосей пятна будет равно β*2α, или, считая, что пятно невелико и угол α мал, равно β*2α = sin ω, где ω - угол, под которым мы смотрим в воду.

Чем меньше этот угол, тем больше вытянуто пятно. Если взгляд скользит по поверхности, то пятно света будет до бесконечности вытягиваться и суживаться.

Рис. 3. Скорость ветра (слева направо): 12 м/с; 12 м/с; 5 м/с; 2 м/с. Высота солнца над горизонтом: 30°; 20°; 13°; 7°

При наблюдении световых дорожек на поверхности моря угол со обычно мал - световые дорожки достигают горизонта (см. рис. 3), так что можно говорить только о ширине дорожки. И хотя полученные нами формулы буквально не применимы в этом случае, пользуясь ими, можно не только качественно объяснить происхождение дорожек, но и понять зависимость их ширины от силы ветра и высоты солнца над горизонтом: с увеличением α и h ширина дорожки возрастает.