Силы инерции во вращающейся системе отсчета

Силы инерции приходится вводить в любой системе отсчета, движущейся относительно Солнца (точнее говоря, относительно так называемой системы неподвижных звезд) с ускорением. Такие системы называют неинерциальными системами в отличие от инерциальных систем/движущихся относительно Солнца и звезд равномерно и прямолинейно.

Земля, строго говоря, не является инерциальной системой отсчета так как она вращается вокруг Солнца и вокруг своей оси. Однако ускорениями, связанными с этими движениями, обычно можно пренебречь и пользоваться в системе Земли законами Ньютона. Но вот поворот маятника Фуко как раз объясняется действием особой силы инерции - силы Кориолиса. Поговорим о ней подробнее.

Рассмотрим простой пример вращающейся'системы отсчета, в которой наглядно проявляются силы инерции.

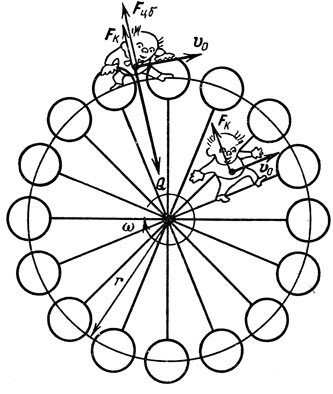
Рис. 2. Силы инерции во вращающейся системе отсчета

Представьте себе, что человек катается на карусели (обозначим ее угловую скорость вращения через ω, а радиус - r). Обсудим случай, когда он еще и перебирается из одного кресла в другое (см. рис. 2), то есть движется в системе карусели по окружности с некоторой скоростью v₀, например, в сторону вращения (эксперимент чисто мысленный, так как это строжайше запрещено правилами).

Рассмотрим вначале движение человека в неподвижной системе отсчета. Полная скорость его движения v складывается из линейной скорости карусели ωr и скорости относительного движения v₀:

Центростремительное ускорение определяется известной формулой

По второму закону Ньютона

где Q - горизонтальная составляющая силы реакции, действующей на человека со стороны кресла карусели. Теперь рассмотрим это же движение в системе карусели. Там скорость равна v₀, и центростремительное ускорение a'_цс = ^v2₀/_r. Используя предыдущие два равенства, можно записать

Если мы хотим пользоваться законом Ньютона и во вращающейся системе, надо ввести силу инерции

где знак "минус" указывает, что эта сила направлена от центра вращения. Сила инерции как бы отбрасывает человека от центра, когда он катается на карусели. Однако слова "как бы" стоят здесь не случайно. Никаких новых сил взаимодействия между телами во вращающейся системе отсчета не возникает. На человека по-прежнему действует со стороны кресла та же сила реакции, имеющая ту же горизонтальную составляющую Q, направленную к центру вращения. Но если в неподвижной системе сила Q создавала полное центростремительное ускорение а_цс, то во вращающейся системе величина ускорения уменьшилась. Поэтому и пришлось ввести силу инерции F_ин, частично компенсирующую силу Q.

В нашем случае сила инерции складывается из двух сил, соответствующих двум слагаемым в выражении для F_ин. Первое - это центробежная сила инерции FцбΡ. Она тем больше, чем быстрее вращение и чем дальше отстоит тело от центра. Вторая сила называется кориолисовой силой F_K (по имени французского ученого Кориолиса, впервые ее рассчитавшего). Такую силу приходится вводить только тогда, когда тело движется во вращающейся системе. Она не зависит от положения тела, но зависит от скорости его движения и от скорости вращения системы отсчета.

Если тело во вращающейся системе движется не по окружности, а, например, по радиусу (см. рис. 2), то оказывается, и в этом случае также необходимо ввести силу Кориолиса. Но направлена она будет не вдоль радиуса, а перпендикулярно ему. И вообще при любом движении во вращающейся системе кориолисова сила направлена перпендикулярно оси вращения и скорости тела. Удивительно, но факт: при движении во вращающейся системе сила инерции не только отбрасывает тело от центра, но и как бы толкает его вбок.

Подчеркнем, что происхождение силы Кориолиса такое же, как и всех сил инерции - эта сила не связана с непосредственным взаимодействием тел. Вот наглядный тому пример.

Представьте себе, что на полюсе установлена пушка, которая стреляет вдоль меридиана (полюс взят для простоты рассуждения). Цель находится на том же меридиане. Может ли снаряд попасть в цель? Если смотреть на стрельбу со стороны (пользоваться инерциальной системой отсчета, связанной с Солнцем), то ситуация ясная: траектория снаряда лежит в начальной меридиональной плоскости, а цель вместе с Землей поворачивается. Поэтому снаряд никогда не попадет в цель (разве что Земля успеет повернуться под ним на целое число суток). А как объяснить то же явление в системе отсчета, связанной с Землей? Как объяснить эффекты, обусловленные "уходом" цели из плоскости полета снаряда? Для этого и приходится вводить кориолисову силу, направленную перпендикулярно скорости тела и оси вращения. Тогда и в системе отсчета, связанной с Землей, становится понятным, почему снаряд выталкивается из меридиональной плоскости и не попадает в цель.

Точно так же объясняется поворот плоскости колебаний и маятника Фуко, о котором мы говорили в начале статьи. В инерциальной системе Солнца плоскость колебаний маятника остается неизменной, а Земля вращается. Поэтому относительно Земли плоскость колебаний поворачивается. (Проще всего опять представить себе, что маятник колеблется на полюсе; тогда плоскость колебаний совершит полный оборот как раз за сутки.) А вот в системе отсчета, связанной с Землей, это явление можно объяснить только с помощью силы Кориолиса.