Мыльные пузыри

"Выдуйте мыльный пузырь и смотрите на него: вы можете заниматься всю жизнь его изучением, не переставая извлекать из него уроки физики",- писал великий английский физик лорд Кельвин. В частности, мыльная пленка является прекрасным объектом для изучения поверхностного натяжения. Сила тяжести здесь практически роли не играет, так как мыльные пленки чрезвычайно тонки и их масса совершенно ничтожна. Поэтому основную роль играют силы поверхностного натяжения, благодаря которым форма пленки всегда оказывается такой, что ее площадь минимально возможная в данных условиях.

Однако почему пленки обязательно мыльные? Почему бы не изучать пленку из дистиллированной воды, ведь ее коэффициент поверхностного натяжения в несколько раз превышает коэффициент поверхностного натяжения мыльного раствора.

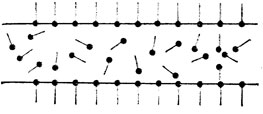
Рис. 1

Дело, оказывается, вовсе не в величине коэффициента поверхностного натяжения, а в структуре мыльной пленки. Мыло богато так называемыми поверхностно-активными веществами, концы длинных молекул которых по-разному относятся к воде: один конец охотно соединяется с молекулой воды, другой к воде безразличен. Поэтому мыльная пленка обладает сложной структурой: образующий ее мыльный раствор как бы "армирован" частоколом упорядочение расположенных молекул поверхностно-активного вещества, входящего в состав мыла^* (рис. 1).

^* (См. книгу: Гегузин Я. Е. Пузыри.- М.: Наука, 1985.- Библиотечка "Квант", вып. 46.)

Вернемся к мыльным пузырям. Наверное, каждому доводилось не только наблюдать эти удивительно красивые творения, но и пускать их. Они сферичны по форме и долго могут свободно парить в воздухе. Давление внутри пузыря оказывается больше атмосферного. Избыточное давление обусловлено тем обстоятельством, что мыльная пленка, стремясь еще больше уменьшить свою поверхность, сдавливает воздух внутри пузыря, причем чем меньше его радиус R, тем большим оказывается избыточное давление внутри пузыря. Определим величину этого избыточного давления ΔP_сф.

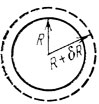
Рис. 2

Поставим мысленный опыт. Пусть поверхностное натяжение пленки пузыря чуть-чуть ослабело, в результате чего его радиус увеличился на величину δR<<R (рис. 2). При этом его внешняя поверхность возрастает на

(S = 4πR² - поверхность сферы), а следовательно, увеличивается и поверхностная энергия пузыря:

(поскольку δЕ уже пропорционально малой величине δR, то изменением коэффициента поверхностного натяжения здесь можно пренебречь).

Заметьте, что в выражении (*) появилась двойка, которой нет в определении поверхностной энергии. Ею мы учли тот факт, что у мыльного пузыря имеется две поверхности - внешняя и внутренняя; при увеличении его радиуса на δR площадь каждой из них возрастает на 8πRδR.

Увеличение поверхностной энергии пузыря произошло за счет работы сжатого в нем воздуха. Считая, что давление в нем при столь малом изменении объема не меняется, можем записать

Изменение объема пузыря определяется объемом тонкостенной сферы (рис. 2):

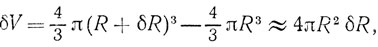
откуда для δЕ находим

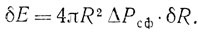
Сравнивая это выражение с найденной ранее формулой (*), получаем, что обусловленное поверхностным натяжением избыточное давление внутри сферического мыльного пузыря

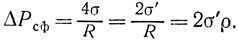
Через σ' = 2σ мы обозначили удвоенный коэффициент поверхностного натяжения жидкости. Понятно, что если бы речь шла об избыточном давлении под одинарной искривленной поверхностью (например, внутри сферической капли жидкости), то оно определялось бы выражением ΔР_изб = ^2σ/_R. Входящая в это выражение величина, обратная радиусу сферы, называется кривизной сферы: ρ = ¹/_R.

Рис. 3

Итак, мы пришли к важному заключению о том, что избыточное давление пропорционально кривизне сферы. Однако сфера - не единственная форма, которую можно придать мыльному пузырю. Если поместить пузырь между двумя кольцами, то его можно растягивать, пока он не примет форму цилиндра со сферическими "шапками" (рис. 3).

Чему равно избыточное давление внутри такого пузыря? У цилиндрической поверхности кривизна в различных направлениях различна. Вдоль образующей цилиндра кривизна равна нулю (образующая - прямая линия)^*, а в сечении, перпендикулярном оси цилиндра, его кривизна равна ¹/_R, где R - радиус цилиндра. Какое же значение ρ мы должны подставить в предыдущую формулу? Оказывается, разность давлений по разные стороны любой поверхности определяется ее средней кривизной. Что же это за величина?

^* (Что такое кривизна плоской кривой? Кривизна окружности определяется так же, как и кривизна сферы: ρ_окр = ¹/_R, где R - радиус окружности. Если же кривая не является окружностью, то, тем не менее, ее отдельные маленькие участки можно приближенно считать дугами окружностей определенных радиусов. Величины, обратные этим радиусам и называются кривизнами плоской кривой в различных ее точках.)

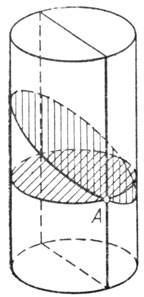
Рис. 4

Проведем через нормаль к поверхности в точке А плоскости. Сечения цилиндрической поверхности этими плоскостями (они называются нормальными сечениями) могут быть окружностью, эллипсом или прямой (рис. 4). Легко видеть, что кривизны этих сечений в точке А различны: максимальной кривизной обладает поперечное сечение - окружность, а минимальной, равной нулю,- прямая (продольное сечение). Средняя кривизна ρ_ср определяется как полусумма максимальной и минимальной кривизны нормальных сечений:

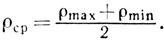
Это определение годится не только для цилиндра; так можно определять среднюю кривизну в данной точке любой поверхности.

У цилиндрической поверхности в любой точке максимальная кривизна ρ_max = ¹/_R, где R - радиус поперечного сечения цилиндра, а ρ_min = 0. Поэтому средняя кривизна цилиндра ρ_ц = ₁/_2R, а избыточное давление внутри цилиндрического пузыря ΔР_ц = ^σ'/_R.

Как видно, у цилиндрического пузыря избыточное давление такое же, как у сферического пузыря вдвое большего радиуса. Поэтому радиус сферических "шапок" у цилиндрического пузыря будет вдвое больше, чем радиус цилиндра, и они являются сферическими сегментами, а не полусферами.

А что если вообще уничтожить избыточное давление в таком пузыре, заставив, например, лопнуть "шапки"? Казалось бы, так как внутри пузыря нет никакого избыточного давления, поверхность его не должна иметь кривизны. А тем не менее стенки пузыря изгибаются внутрь, и пузырь принимает форму катеноида (от латинского слова "катена" - цепь; эту поверхность можно получить вращением вокруг оси кривой, имеющей формуя подвешенной горизонтально за концы цепи - цепной линии). В чем же Я тут дело?

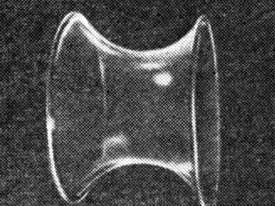
Рис. 5

Присмотритесь к этой поверхности (рис. 5). Обратите внимание на ее узкое место - перехват. Легко видеть, что этот перехват является одновременно и выпуклым, и вогнутым. Его поперечное сечение - окружность, а продольное - цепная линия. Кривизна направления внутрь должна увеличивать давление внутри пузыря, кривизна же направления наружу должна уменьшать его. (Давление под вогнутой поверхностью больше, чем над ней.) В случае катеноида эти кривизны одинаковы по величине, и так как направлены они в противоположные стороны, средняя кривизна равна нулю. Следовательно, внутри такого пузыря нет избыточного давления.

Существует множество других поверхностей, которые кажутся кривыми во всех направлениях, но тем не менее их средняя кривизна равна нулю, и эти поверхности не производят никакого давления. Чтобы получить их, достаточно взять любую гнутую проволочную рамку и погрузить ее в мыльную воду. Вынимая рамку, можно увидеть разнообразные поверхности с нулевой средней кривизной, форма которых зависит от формы рамки. Однако катеноид - единственная, кроме плоскости, поверхность вращения с нулевой средней кривизной.

Одной из задач специальной математической науки - дифференциальной геометрии - является отыскание таких поверхностей с нулевой средней кривизной, натянутых на замкнутые пространственные кривые. Существует точная математическая теорема, утверждающая, что площадь таких поверхностей среди прочих поверхностей, натянутых на ту же кривую, всегда минимальна, и она нам покажется теперь очевидной.

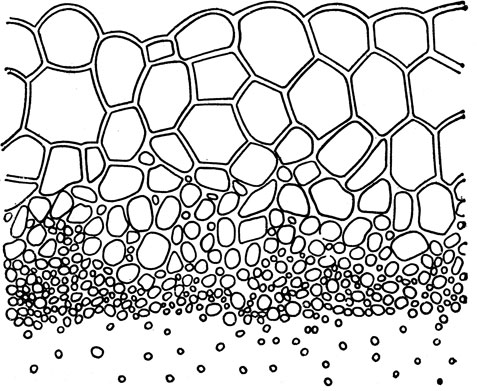
Рис. 6

Мыльные пузыри могут соединяться друг с другом, образуя пену. Несмотря на кажущуюся хаотичность в расположении мыльных пленок в пене, всегда выполняется такой закон: пленки пересекают друг друга лишь под равными углами (см. рис. 6).

Рассмотрим, например, два пузыря, находящихся в контакте друг с другом и имеющих общую перегородку (рис. 7).

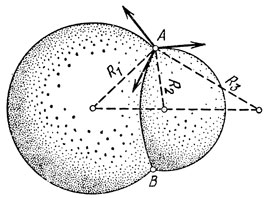
Рис. 7

Избыточные (по сравнению с атмосферным) давления внутри пузырей различны и определяются формулой Лапласа:

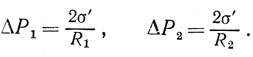
Поэтому перегородка должна быть такой, чтобы создавать дополнительное давление внутри пузырей. Следовательно, три пузырей. Следовательно, она должна обладать определенной кривизной. Радиус R₃ кривизны перегородки определяется из соотношения

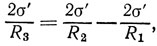
то есть

На рис. 7 изображен разрез пузырей в плоскости, проходящей через их центры. Точки А и В представляют собой точки пересечения с плоскостью чертежа окружности, по которой соприкасаются два пузыря. В любой точке этой окружности встречаются три пленки. Так как их поверхностное натяжение одинаково, то силы их поверхностного натяжения могут "уравновесить" друг друга лишь в том случае, когда углы, под которыми они пересекаются, равны между собой, и следовательно, каждый равен 120°.