Какие бывают капли

Сложнее обстоит дело с формой капель. Стремлению поверхностного натяжения уменьшить поверхность жидкости здесь обычно противодействуют другие силы. Например, капля жидкости почти никогда не является шаром, хотя шар имеет наименьшую из всех фигур поверхность при заданном объеме. Когда капля покоится на неподвижной горизонтальной поверхности, она оказывается сплющенной. Сложную форму имеет и падающая в воздухе капля. И только капля, находящаяся в невесомости, принимает совершенную сферическую форму.

Устранить действие силы тяжести при изучении поверхностного натяжения жидкостей впервые догадался в середине прошлого века бельгийский ученый Ж. Плато. Разумеется, в то время и не мечтали о настоящей невесомости, и Плато просто предложил уравновесить силу тяжести архимедовой выталкивающей силой. Он поместил исследуемую жидкость (масло) в раствор, обладающий такой же плотностью, и, как пишет его биограф, с удивлением увидел, что масло приняло сферическую форму; он тотчас же применил свое правило "вовремя удивляться", и это явление послужило затем для него предметом долгих размышлений".

Свой метод Плато применил для исследования различных явлений. Например, он изучил процесс образования и отрыва капли жидкости на конце трубки.

Обычно, как бы медленно мы ни увеличивали каплю она отрывается от трубки так быстро, что глаз не может уследить за деталями этого процесса. Плато помещал конец трубки в жидкость, плотность которой была только немного меньше плотности капли. Действие силы тяжести при этом ослаблено, поэтому можно вырастить очень большую каплю и увидеть, как она отрывается от трубки.

Рис. 8

На рис. 8 показаны различные стадии красивого процесса образования и отрыва капли (фотографии получены современным методом - с помощью скоростной киносъемки). Попробуем объяснить это явление. Пока капля растет медленно, можно считать, что в каждый момент времени она находится в равновесии. Тогда при заданном объеме капли ее форма определяется из условия, что сумма поверхностной энергии и потенциальной энергии капли, обусловленной силой тяжести, минимальна. Поверхностное натяжение вызывает сокращение поверхности капли, оно стремится придать капле сферическую форму. Сила тяжести, наоборот, стремится расположить центр масс капли как можно ниже. В результате капля оказывается вытянутой.

Чем больше капля, тем большую роль играет потенциальная энергия силы тяжести. Основная масса по мере роста капли собирается внизу, и у капли образуется шейка (вторая фотография на рис. 8). Сила поверхностного натяжения направлена вертикально по касательной к шейке. Она уравновешивает силу тяжести, действующую на каплю. Теперь достаточно капле совсем немного увеличиться, и силы поверхностного натяжения уже не смогут уравновесить силу тяжести. Шейка капли быстро сужается (третья фотография на рис. 8), и в результате капля отрывается (четвертая фотография). При этом от шейки отделяется маленькая капелька, которая падает вслед за большой. Вторичная капелька образуется всегда (ее называют шариком Плато), но так как процесс отрыва капли очень быстрый, обычно мы этой вторичной капельки не замечаем.

Мы не будем здесь вдаваться в причины образования маленькой капельки - это довольно тонкий вопрос. Но попробуем объяснить форму падающей капли. Мгновенные фотографии падающих капель показывают, что маленькие капли почти сферические, а большие похожи на сдобную булочку. Давайте прежде всего оценим радиус капли, при котором она теряет свою сферичность.

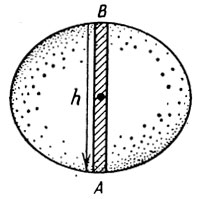
Рис. 9

При равномерном движении капли сила тяжести, действующая, например, на центральный столбик капли АВ (рис. 9), должна быть уравновешена силами поверхностного натяжения. А для этого необходимо, чтобы радиусы кривизны капли в точках А и В были разными. Действительно, поверхностное натяжение создает избыточное давление, определяемое формулой Лапласа: ΔP_л = ^σ'/_R, и если кривизна поверхности капли в точке А будет большей, чем в точке В, то разность лапласовских давлений сможет уравновесить гидростатическое давление жидкости:

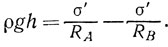
Существенно ли различие R_A и R_B? Для маленьких капель радиусом порядка 1 мкм (10^-6м) величина pgh≈2*10^-2 Па, а величина ΔP_л = ^σ'/_R ≈1,6*10⁵ Па! В этом случае гидростатическое давление настолько мало, по сравнению с лапласовским, что им и вовсе можно пренебречь. Такая капля может считаться эталоном сферичности.

Иное дело для капли диаметром, скажем, 4 мм. Для нее гидростатическое давление pgh≈40 Па, а лапласовское ΔР_л = 78 Па. Эти величины одного порядка, и нарушения сферичности для такой капли более существенны. Полагая R_B = R_A+δR и R_A + R_B = h = 4 мм, найдем, что δR ∼ h(√((ΔP_л/_ρgh)²+1) - ΔP_л/_ρgh) ≈ 1 мм. Разность радиусов кривизны в точках А и В в этом случае оказывается уже порядка самого размера капли.

Наш расчет показывает, для каких капель можно ожидать нарушения сферичности, но форма падающей капли получается обратной наблюдаемой в эксперименте (на фотографии капли сплющены снизу). В чем же дело? А в том, что мы считаем давление воздуха над каплей и под ней одинаковым. При медленном движении капли так и бывает. Но если капля движется в воздухе с достаточно большой скоростью, то воздух не успевает плавно обтекать каплю: перед нею создается область повышенного давления, а за нею - пониженного (там образуются вихри). Разность давлений воздуха может быть больше, чем гидростатическое давление, и лапласовское давление теперь должно скомпенсировать именно эту разность. В таком случае величина давления ^σ'/_RA-^σ'/_RB становится отрицательной и, следовательно, радиус R_A будет больше, чем R_B. Об этом и свидетельствуют фотографии.

А видели вы когда-нибудь очень большие капли? В обычных условиях таких капель нет. И это не случайно - капли большого диаметра неустойчивы и разрываются на маленькие. Сохранность формы капли на несмачиваемой поверхности обеспечивает поверхностное натяжение. Однако когда гидростатическое давление становится больше лапласовского, капля растекается и дробится на более мелкие. Оценить предельно возможный размер капли позволяет неравенство ρgh≥^σ'/RΡ, где h~2R. Отсюда получаем

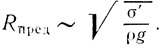
Для воды, например, R_пред≈0,3 см (разумеется, это лишь порядковая оценка максимального размера капли). Вот почему вы не увидите на листьях деревьев и других поверхностях, не смачиваемых водой, слишком крупных капель.