
Пока чайник не закипел...
Тут Алису осенило: - Поэтому здесь и накрыто к чаю?- спросила она. - Да,- отвечал Болванщик со вздохом,- здесь всегда пора пить чай. Мы не успеваем даже посуду вымыть.
Ритуалу чаепития посвящены восточные трактаты и главы в специальных книгах. И все же, посмотрев на этот процесс под несколько иным углом зрения, в нем можно найти множество интересных физических явлений, объяснения которым нет даже в самом толстом кулинарном руководстве.
Для начала проделаем следующий опыт. Поставим два совершенно одинаковых чайника с равными количествами холодной воды на конфорки одинаковой мощности. Один из них закроем крышкой, а второй оставим открытым. Какой из них закипит раньше?
Ответ на этот вопрос знает любая опытная хозяйка. Желая вскипятить воду побыстрее, она, не задумываясь, накрывает кастрюлю крышкой, и на поставленный вопрос сразу же ответит, что скорее закипит чайник, накрытый крышкой. Ну, что же, убедимся в ее правоте - вначале опытным путем, дождавшись кипения наших чайников, а потом обоснуем результат поставленного опыта с точки зрения молекулярной физики.
Пока чайники нагреваются, поставим на третью конфорку плиты еще один точно такой же чайник с тем же количеством холодной воды, что и в первых двух, и попробуем его вскипятить быстрее (при той же мощности конфорки). Для этого нужно каким-либо способом быстро повысить температуру воды в нем, обогнав ее нагрев в двух первых чайниках. Например, сунуть в стоящий на плите третий чайник еще и кипятильник. Ну, а если кипятильника нет?
Вспомним, что для того чтобы повысить температуру воды в какой-либо емкости, в нее достаточно добавить более горячей воды. Может быть, такой прием ускорит закипание воды в третьем чайнике? Отнюдь нет. Не только не ускорит, но еще и замедлит. Чтобы убедиться в этом, представим себе, что вода массой m1, находящаяся первоначально в чайнике при температуре Т1, не смешалась и не стала обмениваться теплом с долитой горячей водой массой m2 и температурой T2. Тепло, которое необходимо было первоначально передать воде для доведения ее до кипения, составляет Q1 = cm1 (Тк-T1). Теперь же, кроме нагрева до температуры кипения (Тк) того же количества воды m1, придется разогреть от Т2 до Тк еще и долитую горячую воду массой m2. Поэтому полное количество теплоты составит
Q = cm1 (Тк-T1) + cm2 (Тк-T2).
Даже если в чайник доливать кипяток, то в процессе переливания он успеет несколько охладиться, и температура Т2 окажется несколько ниже Тк. Понятно, что наше "абсурдное" предположение о том, что порции воды остались неперемешанными, никак не повлияло на закон сохранения энергии в системе, а лишь позволило нам рассмотреть явление проще и быстрее.
Пока мы безуспешно возились с третьем чайником, первый, с закрытой крышкой, уже начинает шуметь. Попробуем выяснить причину этого знакомого всем шума и оценить его характерную частоту.
Первой причиной этого шума можно предположить колебания жидкости, возникающие при отрыве пузырьков пара от дна и стенок сосуда. Эти пузырьки чаще всего зарождаются на неоднородностях и микротрещинках поверхности. Характерные их размеры до закипания чайника порядка 1 мм (при кипении они значительно возрастают и могут доходить до 1 см). Для оценки частоты возникающего в чайнике звука нам нужно найти время отрыва пузырьков τ от дна. Именно это время характеризует длительность толчка, который получает жидкость в процессе отрыва пузырька, а следовательно, и период возникающих в жидкости колебаний. Соответственно частота генерируемого звука определится величиной, обратной этому времени: v∼τ-1.
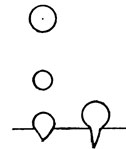
Рис. 1
Пока пузырек пребывает на дне в покое, на него действуют две силы: выталкивающая его вверх сила Архимеда FA = ρBgVn (Vn - объем пузырька) и удерживающая на дне сила поверхностного натяжения Fn = σl (l - длина границы соприкосновения пузырька с поверхностью дна чайника)*. По мере увеличения объема пузырька сила Архимеда возрастает и в некоторый момент превышает силу поверхностного натяжения. Пузырек начинает свое движение вверх (рис. 1). Понятно, что полная сила, действующая на пузырек в процессе его отрыва от дна, по порядку величины равна FA. Масса же пузырька при его движении в жидкости определяется не его собственной ничтожно малой массой (массой заключенного в нем воздуха и пара), а так называемой "присоединенной" массой, которая для сферического пузырька составляет m* = 2/3πρBr03 (в этой формуле ρв - плотность воды, а r0 - радиус пузырька). Она фактически определяет ту массу жидкости вокруг пузырька, которая оказывается вовлеченной в движение при его перемещении вверх.
* (Здесь мы пренебрегаем заведомо малой силой тяжести.)
Таким образом, ускорение пузырька на начальном этапе движения будет
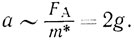
Время отрыва пузырька от дна можно теперь оценить, считая его движение равноускоренным. На высоту порядка своего размера он поднимается за время
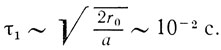
(*)
Соответствующая характерная частота генерируемого при отрыве пузырьков звука составляет v1~τ-1~100 Гц, что, по-видимому, на порядок меньше частоты того звука, который слышен при нагреве чайника (однако еще задолго до закипания воды в нем)*.
* (Заметим, что в выражение (*) никак не вошел коэффициент поверхностного натяжения, поэтому можно думать, что пузырек излучает звуковые волны не только в процессе отрыва от дна, но и в течение всего своего ускоренного движения - до тех пор, пока сила сопротивления движению пузырька со стороны воды (пропорциональная скорости его движения) не уравновесит действующую на него выталкивающую силу.)
Существует и вторая причина шума, возникающего в чайнике при его нагревании. Для того чтобы добраться до нее, проследим судьбу пузырька пара после его отрыва от дна. Оторвавшись от горячего дна, где давление пара в пузырьке было примерно равно атмосферному (иначе он не мог бы достаточно расшириться для всплытия), пузырек, всплывая, попадает в верхние, еще не достаточно прогретые слои воды. Заполняющий пузырек насыщенный пар при этом охлаждается, его давление падает и уже не может компенсировать внешнего давления на пузырек со стороны волы.
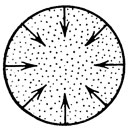
Рис. 2
В результате пузырек быстро схлопывается (рис. 2) или просто сильно сжимается (если в нем, помимо водяного пара, содержалось также некоторое количество воздуха) - в жидкости распространяется звуковой импульс. Схлопывание одновременно большого числа таких пузырьков, гибнущих в верхних слоях воды, воспринимается как шум. Оценим его характерную частоту.
Запишем уравнение Ньютона для массы воды m, устремляющейся внутрь пузырька при его схлопывании:
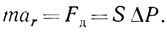
Здесь S = 4πr2 - площадь поверхности пузырька, на которую действует сила давления Fд, ΔР - разность давлений на его границе, аr - ускорение движения границы пузырька к его центру. Понятно, что в процесс такого схлопывания вовлечена масса, по порядку величины равная произведению плотности воды на объем пузырька: m~ρвr3. Таким образом, уравнение Ньютона может быть переписано в виде
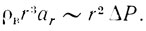
Зависимость давления насыщающих паров от температуры

Пренебрегая давлением, обусловленным натяжением искривленной поверхности пузырька, а также небольшим "количеством воздуха, которое может в нем содержаться, будем считать ΔР постоянным (зависящим только от перепада температур между придонными и верхними слоями воды). Величину ускорения ar = r"t оценим как r0/τ22, где τ2 - искомое время схлопывания пузырька. Тогда
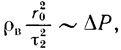
откуда
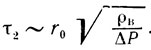
(**)
Вблизи Тк = 100 °С давление насыщенного пара падает примерно на 3*103 Па при понижении температуры на 1 °С (см. таблицу). Поэтому для оценки можно принять ΔР~103 Па, после чего соответствующее время схлопывания пузырька составит τ2~10-3 с, а характерная частота возникающего при этом шума v2∼τ2-1~103 Гц. Этот результат уже больше похож на правду, чем предыдущий.
Еще одним доводом в пользу такого происхождения шума служит тот факт, что по мере повышения температуры воды частота характерного высокочастотного шума постепенно понижается в согласии с (**). Непосредственно перед кипением пузырьки пара перестают схлопываться даже в верхних слоях воды. Тогда единственным механизмом возбуждения звука оказывается рассмотренный выше отрыв пузырьков от дна - частота "пения" чайника заметно понижается. После закипания воды "голос" чайника может снова измениться (особенно если открыть крышку) - это булькают пузыри, лопаясь уже непосредственно на поверхности воды. Здесь оказывается важной и степень заполненности чайника, и его форма.
Таким образом, мы приходим к выводу, что шум чайника перед его закипанием связан с рождением на горячем дне, отрыве от дна и гибелью в верхних, еще не достаточно прогретых слоях воды пузырьков пара. Эти процессы очень интересно наблюдать непосредственно при нагревании воды в стеклянном чайнике с прозрачными стенками. Однако не будем обольщаться, что мы заинтересовались и разобрались в этом вопросе первыми. Еще в XVIII веке шотландский ученый Джозеф Блэк изучал "пение" нагретых сосудов и установил, "что в этом пении участвует дуэт: поднимающиеся пузырьки нагретого воздуха и вибрация стенок сосуда".
И вот, как и ожидалось, первым закипает чайник под закрытой крышкой. Об этом нас извещает вырывающаяся из него носика струя пара. А какова ее скорость?
Эту задачу нетрудно решить, если заметить, что в установившемся процессе кипения практически вся подводимая к чайнику энергия нагревателя расходуется на испарение воды. Филателисты знают, что, когда нужно отпарить марку от конверта, воду наливают лишь на дно чайника, чтобы весь образующийся пар выходил через носик. Будем считать, что и в нашем случае носик свободен и пар выходит наружу только через него. Пусть в результате подвода энергии за время Δt испарится масса воды ΔM. Ее можно определить из уравнения
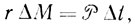
где r - удельная теплота парообразования, а 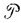 - мощность нагревателя. За это время Δt образовавшаяся масса пара должна покинуть чайник через носик - иначе пар стал бы накапливаться под крышкой. Если площадь выходного отверстия носика s, плотность пара под крышкой чайника ρп(Тк), а искомая скорость v, то можно записать равенство
- мощность нагревателя. За это время Δt образовавшаяся масса пара должна покинуть чайник через носик - иначе пар стал бы накапливаться под крышкой. Если площадь выходного отверстия носика s, плотность пара под крышкой чайника ρп(Тк), а искомая скорость v, то можно записать равенство
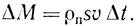
Плотность насыщенного пара при Тк = 373 К можно взять из таблицы (ρп(Тк) = 0,6 кг/м3), или, если таблицы нет под рукой, оценить из уравнения Менделеева - Клапейрона:
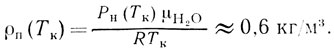
Таким образом, для скорости вытекания пара из носика получаем окончательно
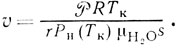
Подставляя сюда для оценки 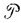 = 500 Вт, s = 2 см2, r = 2,26*106 Дж/кг, ρп(Tк) = 105 Па, находим, что v≈1 м/с.
= 500 Вт, s = 2 см2, r = 2,26*106 Дж/кг, ρп(Tк) = 105 Па, находим, что v≈1 м/с.
И вот, наконец-то, закипает чайник с открытой крышкой. Он заметно отстал от первого. Кстати, снимать с плиты его следует с осторожностью - если просто схватиться за ручку, то можно обжечься паром. А что обжигает сильнее - пар или кипяток? Прежде чем ответить на этот вопрос, следует его уточнить: что сильнее обжигает - определенная масса кипятка или такая же масса пара? Обратимся снова к оценкам.
Пусть объем, занятый насыщенным стоградусным паром под крышкой чайника, составляет V1 = 1 л и, скажем, одна десятая его часть при открывании сконденсируется на руке. Как мы уже выяснили, плотность пара при Tк = 100 °С составляет 0,6 кг/м3. Поэтому на руке окажется около m0≈0,06 г пара. При конденсации и последующем охлаждении от 100 °С до комнатной температуры Т0 будет выделено количество теплоты ΔQn = rmn + cmn(Tк-T0). Легко убедиться, что для того же теплового воздействия понадобится почти в десять раз большая масса кипятка. Кроме того, при ожоге паром значительно большей оказывается площадь поражения. Таким образом, пар обжигает сильнее кипятка, в первую очередь из-за выделяющегося при конденсации значительного тепла.
Но мы отвлеклись от обсуждения результата нашего опыта с двумя чайниками. Почему же все-таки отстал чайник с открытой крышкой? Разберемся в этом подробнее. Ответ почти очевиден: в процессе нагревания воды в открытом чайнике наиболее быстрые ее молекулы имеют возможность беспрепятственно покидать чайник, унося с собой таким образом энергию и как бы эффективно охлаждая этим оставшуюся в чайнике воду (этот процесс есть ни что иное, как испарение). Поэтому нагревателю в этом случае приходится не только довести воду в чайнике до кипения, но и часть ее испарить в процессе нагревания. Понятно, что на это уходит большее количество энергии (а следовательно, и времени), чем при кипячении воды в закрытом чайнике, где вырвавшиеся из воды "быстрые" молекулы очень скоро образуют в замкнутом пространстве под крышкой насыщенный пар и, возвращаясь в воду, отдают свою избыточную энергию обратно. Однако имеют место и два эффекта, противоположных рассмотренному. Во-первых, в процессе испарения несколько уменьшается масса воды, которую следует доводить до кипения. Во-вторых, кипение в открытом чайнике при нормальном атмосферном давлении наступает при температуре 100 °С. В закрытом же чайнике, если он налит так, что пары не могут выходить через носик, из-за интенсивного испарения перед кипением давление у поверхности повышается, поскольку оно теперь определяется суммой парциальных давлений находящегося под крышкой небольшого количества воздуха и самих водяных паров. С ростом внешнего давления должна стать и более высокой температура кипения воды, так как она определяется условием равенства давления насыщенного пара в зарождающемся в жидкости пузырьке внешнему давлению. Как же быть? Какому из эффектов отдать предпочтение?
В случае, когда возникают подобного рода сомнения, на помощь следует призвать точный расчет, или, по крайней мере, оценку порядков величин обсуждаемых эффектов. Вначале оценим массу воды, которая испаряется из открытого чайника в процессе доведения его до кипения.
Молекулы в жидкости достаточно сильно взаимодействуют друг с другом. Однако если в кристалле потенциальная энергия взаимодействия значительно превышает кинетическую энергию движения атомов или молекул, а в газе, наоборот, кинетическая энергия хаотического движения значительно превосходит потенциальную энергию взаимодействия молекул, то в жидкости эти величины оказываются одного порядка. Поэтому молекулы жидкости совершают тепловые колебания около некоторых положений равновесия, изредка "перепрыгивая" в другие. "Изредка" - по сравнению с периодом колебаний около положения равновесия. В привычном же нам масштабе времени очень даже часто - за одну секунду молекула в жидкости может менять свое положение равновесия миллиарды раз! Однако далеко не каждая молекула в процессе своих перескоков, даже находясь у поверхности, может вырваться на свободу. Для преодоления сил взаимодействия ей необходимо иметь возможность совершить некоторую работу. Можно сказать, что потенциальная энергия молекулы в жидкости меньше ее потенциальной энергии в паре на величину, равную теплоте испарения, отнесенной к одной молекуле. Если r - удельная теплота испарения, то молярная теплота испарения равна μr, а теплота испарения, приходящаяся на одну молекулу, составит U0 = μr/NA. Эту "работу выхода" молекула может совершать только за счет своей кинетической энергии теплового движения. Однако соответствующая величина средней кинетической энергии Eк≈kT (k = 1,38*10-23 Дж/К) оказывается значительно меньшей U0. И все же согласно законам молекулярной физики в жидкости всегда существует некоторое количество столь высокоэнергетичных молекул, что они в состоянии преодолеть силы притяжения и вырваться за пределы жидкости. Их число в единице объема определяется выражением
n = n0e-U0/kT(***)
где n0 - начальная концентрация молекул, е = 2,7182... - основание натуральных логарифмов.
Ну, а теперь забудем о перепрыгивании молекул жидкости с места на место, а будем представлять себе высокоэнергетичные молекулы как некоторый газ. Тогда за малое время Δt через участок поверхности площади S смогут вырваться высокоэнергетичные молекулы из объема ΔU~S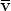 Δt (для оценки мы считаем, что 1/6 часть всех этих молекул приближается к поверхности со скоростью
Δt (для оценки мы считаем, что 1/6 часть всех этих молекул приближается к поверхности со скоростью 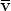 = √(2U0/m0). Воспользовавшись выражением (***), для скорости испарения находим
= √(2U0/m0). Воспользовавшись выражением (***), для скорости испарения находим
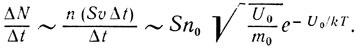
Уносимая при этом из жидкости масса в единицу времени составляет
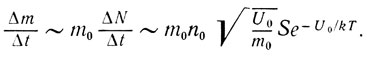
Эту величину нам будет удобнее пересчитать для массы воды, уносимой из чайника при его нагревании на 1 К. Для этого воспользуемся законом сохранения энергии. За время Δt чайник получает от конфорки количество теплоты ΔQ = 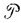 Δt (
Δt (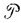 - полезная мощность конфорки). При этом температура воды повышается на ΔT, так что
- полезная мощность конфорки). При этом температура воды повышается на ΔT, так что
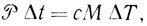
где с и М - теплоемкость и масса воды в чайнике соответственно (теплоемкостью самого чайника мы пренебрегаем). Подставляя в формулу для скорости испарения 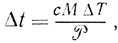 находим, что
находим, что
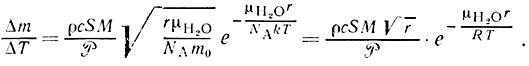
При нагревании чайника температура меняется от комнатной до 373 К. Принимая во внимание, что основная потеря массы происходит при достаточно высоких температурах, подставим в экспоненту некоторую среднюю температуру 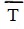 = 350 К. Для остальных величин примем ΔT = Tк-Т0 = 80 К, S ≈ 10-3 м2, ρ≈103кг/м3, μН2О = 0,018 кг/моль, с = 4,19*103 Дж/кг, после чего находим, что
= 350 К. Для остальных величин примем ΔT = Tк-Т0 = 80 К, S ≈ 10-3 м2, ρ≈103кг/м3, μН2О = 0,018 кг/моль, с = 4,19*103 Дж/кг, после чего находим, что
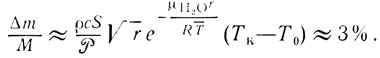
Таким образом, в процессе нагревания чайника без крышки до температуры кипения его покидает несколько процентов всей массы воды. Испарение всей этой массы воды идет за счет нагревателя и, естественно, удлиняет процесс закипания открытого чайника. Чтобы понять, насколько, достаточно заметить, что такое испарение для нагревателя эквивалентно доведению до кипения 1/4 всей массы воды в чайнике (убедитесь в этом сами).
Теперь перейдем к рассмотрению эффектов, замедляющих закипание закрытого крышкой чайника. О первом из них - неизменности массы в процессе нагревания - говорить нечего. Только что было показано, что выкипание 3 % массы эквивалентно нагреву 25 % массы, так что необходимостью нагрева этих 3 % в закрытом чайнике можно пренебречь.
Второй эффект - повышение давления под закрытой крышкой - также не может составить конкуренции выкипанию воды из открытого чайника. Действительно, если даже чайник залит полностью (пар не может выходить через носик), то избыточное, по сравнению с атмосферным, давление не может превысить веса крышки, отнесенного к его площади (в противном случае крышка начнет подпрыгивать, выпуская пар). Принимая, что mкр = 0,3 кг, а ее площадь ~10 см2, получим
ΔP≤mкрg/S≈3H/10-3м2 = 3*103 Па.
Заглянув еще раз в приведенную выше таблицу, видим, что такое повышение давления сдвинет температуру кипения не более чем на δTк≈0,5 °С. Соответственно на доведение чайника до кипения придется затратить дополнительно количество теплоты δQ = cMδTK. Сравнивая величины сМδТк и rΔM, видим, что неравенство rΔМ>>сМδТк выполняется с запасом в 30:1. Таким образом, и повышение температуры кипения в чайнике, прикрытом крышкой и налитом доверху, не может всерьез противостоять испарению воды с открытой поверхности в чайнике без крышки.
На описанном принципе повышения давления при нагревании воды в замкнутом объеме устроена кастрюля-скороварка. В ней вместо носика сделано маленькое отверстие предохранительного клапана, которое открывается только начиная с некоторого давления, в остальном же она герметична. В результате испарения жидкости в замкнутый объем давление в кастрюле повышается примерно до 1,4*105 Па, когда срабатывает клапан, и температура кипения, согласно уже цитировавшейся таблице, сдвигается до Т0к = 108 °С. Это позволяет готовить пищу гораздо быстрее, чем в обыкновенной кастрюле. Однако после снятия с плиты открывать скороварку следует с большой осторожностью: после разгерметизации давление падает и жидкость в ней оказывается заметно перегретой. Поэтому масса жидкости δm такая, что rδm = cM (Т0к-Tк), взрывным образом испаряется и может сильно обжечь. Жидкость при этом вскипает сразу во всем объеме кастрюли.
Кстати, стоит заметить, что высоко в горах, где атмосферное давление низкое, в обычной кастрюле вообще не удается сварить мясо, поскольку температура кипения воды там может понизиться вплоть до 70 °С (на вершине Эвереста давление составляет Р8848 = 3,5*104 Па). Поэтому альпинисты часто берут с собой на восхождение скороварку. Кроме возможности достичь в ней более высокой температуры, скороварка также экономит топливо, что частично ком-пенсирует ее вес в рюкзаке.
Но мы заговорились, а чайники на плите исходят паром. Сняв чайник с закрытой крышкой с плиты, вы видите, что кипеть он прекращает не сразу - некоторое время из его носика еще вырывается струя пара. Какая же часть воды выкипает после снятия чайника с плиты и за какое время?
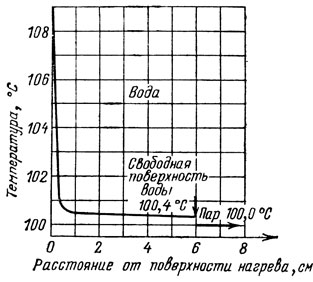
Рис. 3
Для того чтобы ответить на эти вопросы, обратимся к рис. 3, на котором показано распределение температуры воды по высоте при кипении ее в сосуде, к которому через дно подводится тепло. Из рисунка видно, что тонкий придонный слой воды толщиной около 5 мм сильно перегрет - на его протяжении температура падает от Тд = 110°С до Тм = 100,5 °С (Тд - температура дна чайника). Температура остальной массы воды в чайнике (мы предполагаем уровень воды Н = 10 см), согласно графику, составляет около 100,5 °С, а у свободной поверхности жидкости происходит скачок температуры на ΔТ = 0,4 0С.
Таким образом, после прекращения подачи тепла в массе воды запасено избыточное относительно равновесного количество теплоты
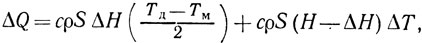
где S - площадь дна чайника (который мы предполагаем цилиндрической формы). Кроме того, перегрето и дно чайника; однако нетрудно убедиться, что этим эффектом можно пренебречь ввиду большой теплоемкости воды.
Избыточное количество тепла ΔQ пойдет на испарение слоя жидкости δН, масса которого δm может быть найдена из уравнения теплового баланса
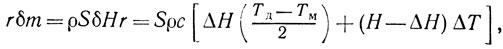
откуда для δH имеем
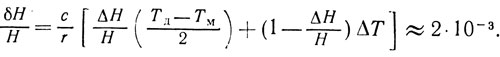
Таким образом, после снятия с плиты из чайника вы-кипит еще около 0,2 % его содержимого.
Характерное время выкипания полного чайника с массой воды М (скажем, 2 кг) на плите с полезной мощностью 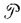 = 1 кВт составляет
= 1 кВт составляет
Соответственно 0,2 % его массы выкипит за время порядка 10 с (если предполагать, что скорость испарения по порядку величины не меняется по сравнению со стационарным режимом).
Рис. 4
Пока мы рассуждали, пришло время разливать чай. Кстати, восточные народы пьют его обычно из пиал. Пиалы, по-видимому, ввели в употребление кочевники - их форма очень удобна при упаковке, они занимают мало места и прочны. Кроме того, они имеют еще одно существенное преимущество перед обычным стаканом. Форма пиалы такова, что верхний слой налитой в нее жидкости, благодаря большому зеркалу поверхности, остывает быстрее, чем в стакане, и его можно пить не обжигаясь. В то же время нижний слой, до которого черед дойдет позже, долго остается горячим. В Азербайджане существует еще более своеобразный сосуд для питья чая - армуди (см. рис. 4). В нем также большое зеркало поверхности сочетается с минимальной поверхностью хранилища горячего чая (нижняя часть сосуда). Старинные фарфоровые чашки также всегда изготовлялись с большим зеркалом поверхности. А стаканы как сосуды для питья чая вошли в обиход в XIX веке в связи с дороговизной фарфоровых чашек. Эти произведения декоративного искусства уступались женщинам, а мужчины пили чай из стеклянных стаканов, которые постепенно обзавелись серебряными подстаканниками с вензелем хозяина.
В заключение подумайте, хороши ли с физической точки зрения серебро и алюминий в качестве материалов для изготовления подстаканников? Каким требованиям должен в первую очередь удовлетворять материал, из которого изготовляется подстаканник?
|
ПОИСК:
|