Плотная упаковка шаров

Можно ли заполнить твердыми шарами все пространство? Разумеется, нет - между ними всегда остаются свободные промежутки. Доля пространства, занимаемая шарами, называется плотностью их упаковки. Чем теснее расположены шары, чем меньше свободного места между ними, тем больше плотность упаковки. Когда же достигается максимальная плотность упаковки одинаковых твердых шаров? Ответ на этот вопрос дает ключ к разгадке "тайны" следов на песке.

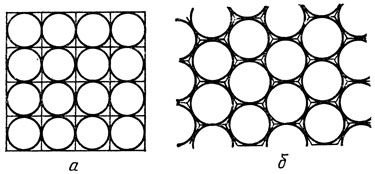
Рис. 1. Упаковка равных кругов на плоскости в ячейки правильных мозаик

Исследуем вначале более простой случай - упаковки одинаковых кругов на плоскости. Плотной упаковки кругов можно достичь, вписывая их в мозаики, составленные из правильных многоугольников, заполняющих всю плоскость. Существуют только три способа построения таких мозаик - из правильных треугольников, квадратов и правильных шестиугольников. Упаковки кругов с использованием квадратной и шестиугольной мозаик показаны на рис. 1. Даже "на глаз" видно, что второй способ (б) более экономичен. Точный расчет (вы вполне сможете провести его сами) показывает, что в этом случае кругами заполнено 90,7 % плоскости, в то время как в первом случае (а) - только около 78 %. Шестиугольный способ упаковки на плоскости - самый плотный. По-видимому, из-за этого его и используют пчелы при построении сот.

Плотную упаковку шаров в пространстве можно осуществить следующим образом. Расположим на плоскости первый слой шаров уже известным нам наиболее плотным способом. Затем можно положить на них второй точно такой же слой. Если располагать каждый шар верхнего слоя в точности над нижним, так что все шары окажутся вписанными в кубические соты, то слишком много пространства окажется неиспользованным. При таком способе укладки шаров заполняется только 52 % пространства.

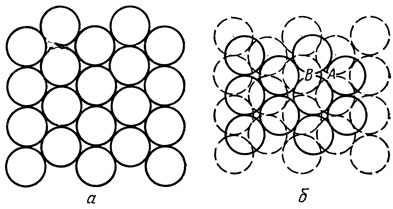
Рис. 2. Плотная упаковка шаров а пространстве (штрихом показан нижний слой)

Ясно, как можно упаковать шары плотнее. Для этого верхний шар надо располагать в лунке, образованной тремя соседними нижними шарами. Но при этом верхние шары не смогут заполнить все лунки - одно из двух соседних углублений всегда остается свободным (рис. 2). Поэтому, когда мы укладываем третий слой шаров, сделать это можно будет двумя способами: либо расположить шары третьего слоя над теми углублениями в первом слое, которые шары второго слоя оставили свободными (центр одного из шаров на рис. 2, б будет находиться в точке А), либо - как раз над шарами первого слоя (при этом центр одного из шаров третьего слоя окажется в точке В). Для последующих слоев порядок расположения шаров сохраняется. В результате получаем два способа плотной упаковки шаров, показанные в пространстве на рис. 3. В обоих случаях шарами заполнено около 74 % пространства.

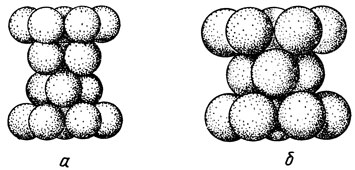
Рис. 3. Пространственная картина, показывающая два способа плотной упаковки шаров

Легко подсчитать, что при таком способе упаковки каждый шар соприкасается с 12 соседними шарами. Точки соприкосновения образуют вершины четырнадцатигранника. Его грани - чередующиеся квадраты и равносторонние треугольники. Так, при втором способе плотной упаковки (рис. 3, б) получается кубоктаэдр, показанный на рис. 4. До сих пор мы рассматривали лишь такие способы упаковки шаров, при которых они вписываются в периодические "соты". А можно ли достичь плотной упаковки, отказавшись от этого условия? Один из способов показан на рис. 5. Шары в каждой плоскости расположены по сторонам правильных пятиугольников (пентагонов). В каждом Пентагоне соседние шары касаются друг друга, но шары, относящиеся к разным пентагонам одной плоскости, разделены в пространстве. Стороны пентагонов чередующихся слоев попеременно содержат четное и нечетное число шаров. Коэффициент заполнения пространства в такой структуре равен 72 % и лишь немного уступает случаю плотной упаковки, показанному на рис. 2. Можно упаковывать шары, не образуя из центров решетку, более плотно, достигнув коэффициента заполнения 74 %, однако существуют ли еще более плотные упаковки - этот вопрос остается открытым до сих пор.

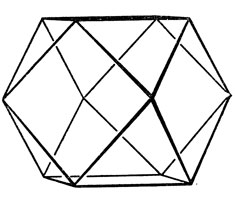
Рис. 4. Кубоктаэдр Кеплера

Вернемся к следам на песке. Мы теперь знаем, что существуют особые упаковки шаров, при которых остается очень мало пустого пространства между ними. Если нарушить такое расположение, выведя, например, шары одного слоя из лунок другого слоя, то промежутки между шарами увеличатся. Ясно, однако, что песчинки никто не упаковывает специальным образом. Как же достичь плотной упаковки песчинок?

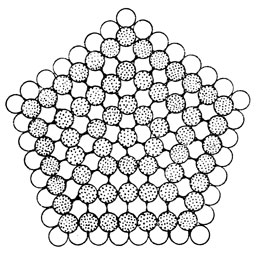
Рис. 5. Пентагональная упаковка шаров

Вспомним житейский опыт. Вам надо заполнить сосуд крупой так, чтобы в него вместилось максимальное ее количество. Что вы при этом делаете? Потряхиваете сосуд или постукиваете по нему, добиваясь желаемого эффекта. Даже после плотной утрамбовки крупы в сосуде можно с помощью такого приема уместить еще какое-то дополнительное ее количество.

Научное исследование этого вопроса предпринял в 50-х годах английский ученый Г. Скотт. Он заполнял шариками от подшипников сферические бутылки разных размеров. Если заполнять бутылки без потряхивания так, чтобы шарики располагались случайным образом, экспериментально наблюдается следующая зависимость плотности упаковки от числа шариков:

где N - полное число шариков. Если число шариков очень велико (а в опытах N достигало нескольких тысяч), то видно, что плотность упаковки стремится стать постоянной и соответствующей заполнению 60 % пространства. А вот если потряхивать бутылку по мере ее заполнения, плотность упаковки возрастает:

Правда, и в этом случае она получается гораздо меньшей 74 %, соответствующих регулярному расположению шариков.

Стоит задуматься над приведенными здесь экспериментами. Почему поправка обратно пропорциональна ³√N? Шарики, расположенные у стенок сосуда, находятся в особом положении по сравнению с шариками в объеме и влияют на плотность упаковки. Величина их вклада пропорциональна отношению площади поверхности (~R²) к объему сосуда (~R³) и убывает обратно пропорционально размеру системы (R). Под объемом системы мы понимаем полный объем пространства, занимаемого шариками вместе со свободными промежутками. Размер R~³√N, так как объем системы пропорционален полному числу шариков. Такие зависимости часто возникают в физике, когда надо учитывать поверхностные эффекты.

Таким образом, точные эксперименты подтверждают житейский опыт и показывают, что, потряхивая зернистую среду, можно достичь большей плотности упаковки. Но почему же все-таки это происходит? Дело в том, что устойчивому положению равновесия всегда соответствует минимум потенциальной энергии. Шарик может устойчиво лежать в ложбинке, но с вершины горки он обязательно скатится. Нечто подобное происходит и здесь. Шарики при потряхивании скатываются в свободные промежутки, плотность упаковки увеличивается, а общий объем системы уменьшается. В результате понижается уровень заполнения сосуда шариками, а следовательно, опускается центр масс и уменьшается потенциальная энергия системы.

Теперь, наконец, можно с достаточной ясностью представить себе, что происходит с песком. Движение воды встряхивает песок, и в результате достигается плотная упаковка песчинок. Сдавливая песок ногой, мы нарушаем эту упаковку и увеличиваем размер пор. Вода из верхних слоев песка уходит вглубь, заполняя эти увеличившиеся промежутки. В результате песок "высыхает". Когда ногу убирают, деформация исчезает, плотная упаковка восстанавливается, а вытесненная из вновь уменьшившихся промежутков вода заполняет след, оставленный ногой. Может случиться и так, что после сильного нажатия плотная упаковка не восстанавливается. Тогда след станет снова мокрым, лишь когда вода поднимется из нижних слоев и заполнит увеличившиеся поры.

Любопытно, что это свойство сыпучих сред знали еще индийские факиры. Один из трюков состоял в том, что в сосуд с узким горлышком, доверху наполненный рисом, многократно втыкали длинный узкий нож. В какой-то момент нож застревал в рисе, и можно было, потянув нож, поднять сосуд с рисом. Ясно, что фокус состоял в том, что сосуд при заполнении рисом встряхивали, достигая плотной упаковки. Втыкание ножа нарушало эту упаковку и увеличивало объем пространства между рисинками. Так как объем сосуда не менялся, то возрастали силы, сдавливающие рисинки, а следовательно, и трение между ними и ножом. В какой-то момент оно оказывалось достаточным, чтобы помешать вытянуть нож из риса.