Квантование магнитного потока

В микромире - мире молекул, атомов, элементарных частиц - многие физические величины могут принимать только определенные дискретные значения; как говорят физики, величины квантуются (например, как уже упоминалось, согласно правилу Бора, дискретна энергия электрона в атоме). В больших коллективах частиц - макроскопических телах - квантовые эффекты обычно перестают быть заметными, поскольку из-за хаотического теплового движения происходит усреднение величины по большому числу ее различных значений и квантовые скачки "замазываются".

А что будет, если тело охладить до очень низких температур? Тогда мириады микрочастиц могут двигаться согласованно и в таком случае квантование проявляется в макроскопических масштабах. Пример тому дает замечательное явление - квантование магнитного потока в сверхпроводнике.

Что такое магнитный поток Ф, знают все, кто изучал явление электромагнитной индукции:

где В - модуль вектора магнитной индукции, a S - площадь поверхности, охватываемой контуром (для простоты будем считать, что индукция направлена по нормали к поверхности). Однако для многих будет открытием, что магнитный поток, создаваемый сверхпроводящим током, текущим, например, по кольцу, может принимать только определенные дискретные значения. Попробуем хотя бы упрощенно понять это явление. Для этого здесь нам будет достаточно воспользоваться представлением о движении микрочастиц по квантовым орбитам, заменяющим при упрощенном рассмотрении облака вероятности.

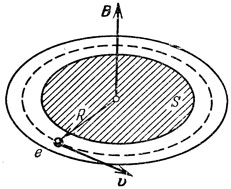
Рис. 1

Движение сверхпроводящих электронов в кольце (рис. 1) похоже на движение электронов в атоме: электроны в кольце как бы движутся по гигантским орбитам радиуса R без всяких столкновений. Поэтому естественно предположить, что их движение подчиняется тем же правилам квантования, что и движение электронов в атоме. Согласно постулату Бора в атоме только определенные орбиты электронов являются стационарными, устойчивыми. Они отбираются с помощью следующего правила квантования: произведение модуля импульса электрона то на радиус орбиты R (величина mvR называется моментом импульса электрона) может принимать только дискретные значения, то есть

Здесь n - целое положительное число, а величина ћ, определяющая наименьшее возможное изменение (квант) момента импульса,- постоянная Планка, с которой мы уже познакомились в разделе "Соотношение неопределенностей". Оказывается, квантование всех физических величин определяется именно этой универсальной постоянной. Найдем величину кванта магнитного потока. Магнитный поток через кольцо связан с током I соотношением

где L - индуктивность кольца. Ток I можно выразить через скорость электронов v и их число N. Действительно, за время t = 2πR/v электроны совершают полный оборот; следовательно, за это время через любое поперечное сечение кольца пройдут все электроны, переносящие заряд q = eN (где е - заряд одного электрона). Поэтому ток в кольце

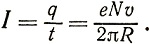
Еще одно соотношение, связывающее величины v, N и I, можно получить, приравнивая кинетическую энергию сверхпроводящих электронов к энергии кольца с током

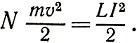
Теперь выражение для магнитного потока можно представить в виде

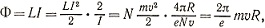
откуда следует, что магнитный поток пропорционален моменту импульса электронов. Но, согласно правилу квантования Бора, момент импульса может принимать только дискретные значения, поэтому и магнитный поток через кольцо, по которому течет сверхпроводящий ток, тоже квантуется:

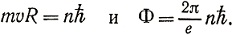
Квант магнитного потока, который можно найти из предыдущей формулы, конечно, очень малая величина (~10^-15 Вб), но тем не менее современные приборы позволяют наблюдать квантование магнитного потока. Такой опыт был проделан американскими учеными Дивером и Фейрбенком в 1961 г., только вместо кольца они использовали полую сверхпроводящую трубку, по которой циркулировали круговые сверхпроводящие токи. В опыте было обнаружено, что магнитный поток через площадь поперечного сечения трубки менялся действительно скачкообразно, однако величина кванта потока оказалась вдвое меньше приведенной выше. Объяснение этому дает современная теория сверхпроводимости. Дело в том, что в сверхпроводящем состоянии электроны объединяются в пары, и именно движением пар, имеющих заряд 2е, создается сверхпроводящий ток. Поэтому правильное значение Ф₀ кванта магнитного потока получается, если в формулу квантования потока подставить удвоенный заряд электрона:

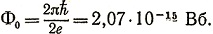
Вот так нашлась двойка, потерянная не только нами, но и английским ученым Лондоном, который теоретически предсказал квантование магнитного потока еще в 1950 г.- задолго до того, как была понята природа сверхпроводящего состояния.

Хочется подчеркнуть, что приведенный здесь вывод квантования магнитного потока хотя и отражает правильно физическую сущность этого явления, но слишком упрощен. Даже удивительно, что таким образом можно получить правильное значение кванта магнитного потока. В действительности сверхпроводимость - сложное квантовое явление. Тем, кто хочет в нем разобраться по-настоящему, предстоит долгий путь, на который потребуется много лет упорного, но увлекательного труда.

БизнесБас Сервис. Профессиональный ремонт форд транзит в сжатые сроки без потери качества.