§ 3. Испускание, поглощение и усиление излучения

Известно, что атомные системы, такие, например, как атомы, ионы и молекулы, могут находиться в определенных стационарных состояниях, каждое из которых соответствует определенному значению энергии. Эти состояния характеризуются квантовыми числами. Значения энергий носят название уровней атомной системы. Если два или большее число состояний имеют одну и ту же энергию, то говорят о вырожденном уровне, и число состояний с одной и той же энергией равно кратности вырождения уровня. Часто слово "состояние" употребляется в смысле уровня; при этом все состояния с одной и той же энергией рассматриваются как идентичные. Переходы между стационарными состояниями могут происходить при испускании или поглощении энергии электромагнитного излучения или при передаче или получении энергии при взаимодействии с другой системой. Если переход носит излучательный характер^*, то частота испущенного или поглощенного системой излучения определяется правилом частот Бора:

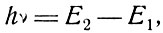
(3.1)

где E₁ и E₂ - энергии состояний, между которыми имеет место переход, h - постоянная Планка.

^* (Имеется в виду излучение электромагнитной волны.- Прим. перев.)

Наинизший энергетический уровень системы называется основным уровнем, а все другие - возбужденными уровнями.

Используются также термины "основное состояние" и "возбужденное состояние". В основном состоянии атом может только поглощать излучение. Мы пронумеруем уровни в порядке возрастания их энергии, начиная от основного уровня. Если атомная система находится не на основном уровне, она может перейти на более низкий уровень без какой-либо связи с имеющимся внешним излучением. Это явление называется спонтанным излучением. Вероятность того, что в единицу времени атом с уровня n перейдет спонтанно на более низкий уровень m, называется вероятностью спонтанного перехода^*. Она обозначается А_nm. Эта величина является характеристикой пары рассматриваемых уровней. В случае кратных уровней величина А_nm определяется суммированием по всем парам состояний. Если рассматривается большое число атомных систем и N_n есть число систем на уровне n, то полное число переходов с уровня n на уровень m будет приближенно равно N_nА_nm в 1 сек, и излученная мощность на частоте v_nm = ^{(E_n - E_m)}/_h будет равна N_n(E_n - E_m)А_nm. Спонтанное излучение испускается ансамблем атомов с беспорядочной фазой, следовательно, ансамбль независимых атомов (газ) будет излучать как некогерентный источник.

^* (Строго говоря, мы имеем дело с величинами, которые должны называться скоростями, а не вероятностями. Их размерность - обратное время. Этот вопрос обсуждается ниже, в конце параграфа.)

Между различными атомными или молекулярными энергетическими уровнями имеют место не только спонтанные, но также и вынужденные переходы, вызванные электромагнитным излучением соответствующей частоты. Полная вероятность того, что атомная система в единицу времени перейдет с уровня n на более низкий энергетический уровень m, определяется как

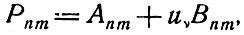
(3.2)

где u_v = плотность излучения на частоте, соответствующей энергии перехода; А_nm и B_nm - постоянные, характеризующие атомную систему. При наличии излучения соответствующей частоты атомная система может также переходить с нижнего на более высокий энергетический уровень. Вероятность такого процесса (поглощения) равна

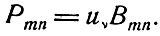
(3.3)

Излучение, испущенное атомной системой при наличии внешнего излучения, состоит из двух частей. Та часть, интенсивность которой пропорциональна А_nm, является спонтанным излучением; его фаза не зависит от фазы внешнего излучения. Часть, интенсивность которой пропорциональна u_vB_nm, является вынужденным излучением; его фаза та же, что и у вызывающего его внешнего излучения.

В конечном счете никакое излучение не является строго монохроматическим. Для простоты мы предположим пока, что спектральная линия каждого атома настолько узка, что распределение энергии по частоте внутри линии не может быть разрешено и мы наблюдаем только полную испускаемую или поглощаемую энергию. Мы предположим также, что плотность излучения u_v меняется незначительно внутри спектральной линии.

Соотношения между величинами А и В известны под названием соотношений Эйнштейна:

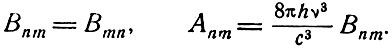
(3.4)

Эти соотношения справедливы в вакууме для частиц, имеющих только невырожденные энергетические уровни. Если энергетические уровни вырождены, то первое соотношение Эйнштейна будет иметь вид [46]

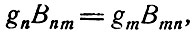
(3.5)

где g_n и g_m - кратности вырождения уровней n и m соответственно. Второе соотношение не зависит от кратности вырождения. В твердых телах, где коэффициент преломления η существенно отличается от единицы, второе соотношение (3.4) должно быть заменено следующим:

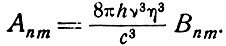
(3.6)

Коэффициент η обусловлен тем, что множитель, стоящий перед B_nm, есть число возможных мод^* в объеме. Волновые же векторы, которые входят в расчеты, определены через частоту и скорость света в веществе.

^* (Под словом "мода" подразумевается определенный тип электромагнитной волны, т. е. один из радиационных осцилляторов.- Прим. ред.)

Действительно, k² = ^(2πv)2/_u², что ведет к замене с в (3.4) на v = с/η.

Пусть имеется большое число атомов N₀. Известно, что в случае термодинамического равновесия при температуре Т, измеряемой в абсолютной шкале, распределение этих атомов между различными состояниями подчиняется закону Больцмана, так что число атомов в состоянии j будет равно

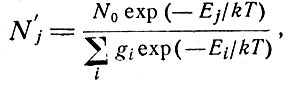
(3.7)

где E_j - энергия в состоянии j. Все состояния с совпадающими энергетическими уровнями заполнены одинаково, следовательно, число атомов на уровне n есть N_n = g_nN_n, где N_n означает степень населенности любого состояния вырожденного уровня n. Из (3.7) следует, что степени населенности энергетических уровней n и m связаны формулой

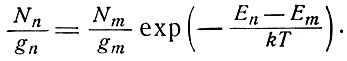
(3.8)

При температуре абсолютного нуля все атомы будут находиться в основном состоянии. В условиях, термодинамического равновесия при любой температуре состояние с низкой энергией должно иметь большую населенность, чем состояние с высокой энергией.

Рассмотрим ансамбль атомов, находящийся вначале при температуре абсолютного нуля. Этот ансамбль будет поглощать только то излучение, частота которого описывается последовательностью (E_i - E₁)/h, где i = 2, 3, ... Если ансамбль находится в термодинамическом равновесии при конечной температуре T, то населено не только основное состояние; следовательно, будет поглощаться излучение, частота которого соответствует переходу между возбужденными состояниями. Следует помнить (как экспериментальный факт), что первые возбужденные уровни большинства атомов и ионов расположены по крайней мере на 2*10^-12 эрг. выше, чем основной уровень, и что для Т = 500° К произведение kT приближенно равно 0,07*10^-12 эрг. Следовательно, при умеренных температурах только незначительная часть атомов будет находиться на первом возбужденном уровне по сравнению с числом атомов в основном состоянии, так как экспоненциальный множитель в (3.8) очень мал. Поглощение излучения за счет переходов с возбужденного уровня будет мало, так как число переходов с уровня n на уровень m пропорционально N_nB_mnu_v.

Вследствие поглощения излучения будет нарушено термодинамическое равновесие внутри ансамбля. Предположим, что поглощается монохроматическое излучение. Атомы, перешедшие за счет поглощения излучения на более высокий возбужденный уровень, чем первый, могут возвратиться в основное состояние с помощью спонтанного или вынужденного излучения или могут перейти на другой энергетический уровень, отличающийся от основного. Таким образом, может возникнуть целый каскад переходов, причем при каждом переходе частота испускаемого излучения отлична от частоты излучения, с помощью которого атомы первоначально были возбуждены с основного состояния. Согласно соотношению (3.1), связывающему энергию и частоту, испущенное при каскадном процессе излучение, которое называется флуоресценцией, имеет более низкие частоты по сравнению с частотой возбуждающего излучения.

Рассмотрим теперь ансамбль, который может не находиться в термодинамически равновесном состоянии, и обозначим опять число атомов в единице объема в состоянии n через N_n. Предполагая n>m, рассмотрим, каков будет результат взаимодействия ансамбля с направленным излучением частоты v_nm и плотности u_v. Число переходов в секунду вниз с уровня n на уровень m будет (A_nm + u_vB_nm)N_n, а число переходов вверх будет u_vB_mnN_m. Когда N_n<N_m, что обычно имеет место, потери падающего пучка будут составлять (N_m - N_n)u_vB_nm квантов в секунду. Испущенные спонтанно A_nmN_n квантов могут рассматриваться как рассеянное излучение. Таким образом, интенсивность пучка, проходящего через вещество, в котором более низкие энергетические состояния населены плотнее, чем более высокие, будет всегда убывать, вещество будет иметь положительный коэффициент поглощения.

Мысленно можно легко построить такой ансамбль, для которого N_n (число атомов в состоянии n) больше, чем N_m, даже если n>m. Говорят, что такой j ансамбль имеет инверсную населенность. Он не находится в термодинамическом равновесии. Предположим, что инверсная населенность получена между двумя уровнями 1 и 2. Это означает, что мы нашли стационарный неравновесный процесс, который приводит к N₂>N₁. В таком положении вещество будет давать спонтанное излучение. Это вещество также будет усиливать излучение соответствующей частоты v = (E₂ - E₁)/h, а спонтанное излучение той же частоты будет восприниматься как шум усилителя.

Чтобы получить количественные соотношения, описывающие процесс усиления, желательно более подробно рассмотреть процесс поглощения и уточнить ту математическую идеализацию, которую мы приняли относительно бесконечно узких уровней и спектральных линий. Найдено, что свет одной и той же интенсивности I₀, но переменной частоты, падающий на поглощающую поверхность, убывает по интенсивности на глубине x согласно закону

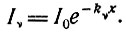
(3.9)

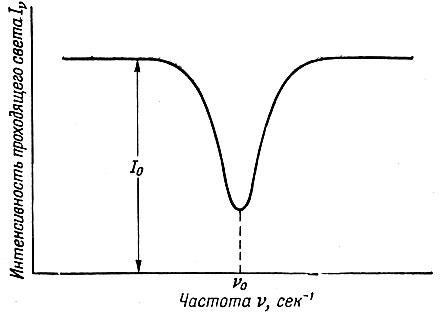
Фиг. 1. Форма линии поглощения

Характер поглощения, определяемый формулой (3.9), обычно имеет вид кривой, представленной на фиг. 1, где изображена интенсивность на заданной глубине поглощающего вещества как функция частоты. Частота v₀ соответствует центру линии поглощения. Если x измеряется в сантиметрах, k_v выражается в см^-1. Путем измерений мы можем получить k_v как функцию частоты, и после того, как это будет сделано, мы получим кривую, аналогичную изображенной на фиг. 2. Полная ширина кривой в том месте, где k_v уменьшается до половины своего максимального значения k_макс называется шириной линии поглощения и обозначается через Δv. Часто эта величина называется "полушириной", что означает не половину ширины кривой, а полную ширину на половине максимума. Мы не будем пользоваться этим термином.

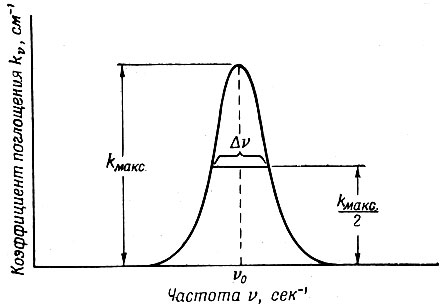
Фиг. 2. Зависимость коэффициента поглощения от частоты для линии поглощения

Важное соотношение связывает полную площадь под кривой фиг. 2 с коэффициентами Эйнштейна и степенью населенности состояний, от которых зависит поглощение на частотах вблизи v₀. Это соотношение было выведено Фюхтбауэром и Ладенбургом в начале двадцатых годов^*. Для знакомства с более подробным и более строгим доказательством, чем представленное здесь, отсылаем читателя к книге Кембла "Квантовая механика" [46].

^* (Представленное доказательство следует методу Митчелла и Земанского [62]. Однако наше определение коэффициентов Эйнштейна отличается на множитель с/4π.)

Рассмотрим параллельный Пучок света с частотой между v и v + dv и интенсивностью I_v, распространяющийся в положительном направлении x через слой атомов, ограниченный плоскостями x и x + dx. Пусть скорость света в веществе есть v = с/η, где η - показатель преломления. Фазовый фронт волны будет проходить через слой толщиной dx за время dt = dx/v. Предположим, что на уровне 1 имеется N₁ атомов на 1 см³, из которых dN_1v атомов участвуют в поглощении на частотах от v до v + dv, а на уровне 2 имеется N₂ атомов на 1 см³, из которых dN_2v атомов участвуют в излучении в той же частотной области. В этом случае, когда фазовый фронт волны пройдет от x до x + dx, уменьшение энергии пучка будет равно

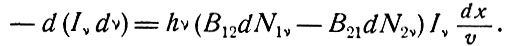
(3.10)

Здесь мы использовали тот факт, что вынужденное излучение когерентно с вызывающим его излучением, следовательно, оно будет усиливать интенсивность пучка. Спонтанное излучение не увеличивает сколь-нибудь существенно интенсивность пучка, так как оно не связано с ним. Из (3.10) следует, что

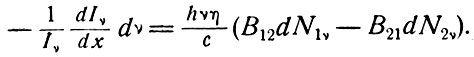
(3.11)

Обозначив левую часть через k_vdv и интегрируя по всей линии с центром в v₀, получим

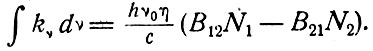
(3.12)

Здесь В₁₂ можно исключить с помощью соотношения (3.5) и В₂₁ можно выразить через А₂₁ путем использования соотношения (3.6). Таким образом, мы получаем формулу Фюхтбауэра - Ладенбурга:

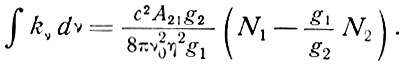
(3.13)

Эту основную формулу перепишем в виде

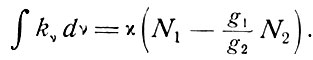
(3.14)

Константа 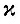может быть записана в различной форме; одна из них следующая:

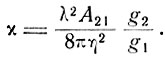
(3.15)

Здесь, как и всюду, мы используем символ λ для обозначения длины волны в вакууме.

Рассмотрим теперь случай, когда уровень 1 является основным уровнем. В возбуждаемых электрическим разрядом газах или в активном веществе лазера, возбуждаемом интенсивным светом, число возбужденных атомов N₂ может составлять значительную долю от полного числа атомов. В этом случае последний член в (3.14) не может быть исключен. Однако если образование возбужденных атомов является результатом поглощения пучка средней интенсивности, то отношение N₂/N₁ чрезвычайно мало. Следовательно, (3.14) можно записать в виде

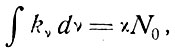
(3.16)

где величина N₁ заменена полным числом атомов N₀. Интересно заметить, что при описанных условиях интеграл от коэффициента поглощения просто пропорционален числу присутствующих атомов и его величина не зависит от формы линии. Константа 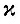есть интегральное поперечное сечение поглощения на один атом для рассматриваемой линии; величина σ_v = k_v/N₀ - поперечное сечение поглощения атома.

Когда вещество находится в термодинамическом равновесии, распределение атомов по уровням описывается соотношением (3.8). Для любого положительного значения абсолютной температуры имеем

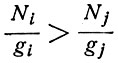
(3.17)

для любых E_j>E_i.

Неравновесное состояние, для которого неравенство (3.17) носит обратный характер, в литературе часто называется состоянием с отрицательной температурой. Отрицательная величина Т вычисляется из распределения атомов по энергетическим уровням с помощью формулы Больцмана (3.8). Рассматриваются только пары уровней, и отрицательное значение температуры вытекает из использования этой формулы для пары уровней системы, не находящейся в термодинамическом равновесии. Определенная таким образом температура не имеет обычного смысла, так что kT/2 уже не есть средняя энергия системы на каждую степень свободы, и ничего нельзя сказать о значении Т для распределения населенности в других состояниях, кроме той пары, для которой это отрицательное значение было вычислено. С точки зрения автора использование термина "отрицательная температура" не способствует пониманию явления неравновесных состояний, и поэтому мы будем избегать этого термина и говорить вместо этого об инверсной населенности. Понятие отрицательной температуры введено здесь только для того, чтобы осуществить связь с принятым в литературе термином. Выражение "существует отрицательная температура Т для уровней n и m" означает только, что для E_n>E_m имеет место неравенство N_n>N_m и что величина Т определена соотношением (3.8).

Когда имеет место инверсная населенность уровней n и m, соотношение (3.14) дает отрицательную величину для интегрального коэффициента поглощения. Условия существования отрицательного поглощения означают усиление. Отрицательное поглощение, или усиление, есть результат превышения вынужденного излучения над поглощенным. В веществе, которое имеет отрицательный коэффициент поглощения в некоторой частотной области, первоначальная световая волна будет возрастать согласно закону (3.9), который в этом случае выражает экспоненциальный рост со скоростью α = - k_v.

Теперь мы обратимся к концепции времени жизни, которая часто используется при описании переходов между различными состояниями атома. Время жизни какого-либо состояния просто связано с вероятностью перехода из этого состояния. Пусть р - вероятность того, что атом в состоянии s в некоторый момент времени покинет это состояние за единицу времени. Эта единица должна быть выбрана таким образом, чтобы p<<1. Тогда из большого числа атомов N, первоначально находящихся в состоянии s, только W(1-р)^t атомов останется в том же состоянии через t единиц времени. Так как для малого значения р мы можем написать (1-p)^t ≈ ехр(-pt), то число атомов, остающихся через t единиц времени, приближенно равно N(t) = Nexp(-pt). Следовательно, число атомов, покидающих состояние s в интервале времени от t до t + dt, равно pN exp(-pt)dt. Таким образом, среднее время жизни атома в состоянии s есть

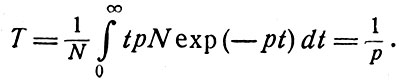
(3.18)

Из выражения (3.18) следует, что обратная величина вероятности перехода называется временем жизни. Если переход из определенного атомного состояния может происходить в результате различных процессов, характеризуемых временами жизни τ₁, τ₂, ..., τ_n и эти процессы статистически независимы, то время жизни данного состояния связано с временами жизни для этих процессов соотношением

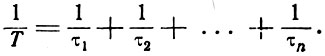
(3.19)

В литературе обычно используются времена жизни вместо вероятностей перехода. Таким образом, обозначив А₂₁ = τ^-1, интегральное поперечное сечение поглощения 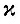можно записать в форме

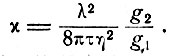
(3.20)

Прежде чем закончить этот раздел, мы обратим внимание на некоторые общие свойства атомов, которые определяют значения коэффициентов Эйнштейна и времена жизни. До сих пор мы упрощали рассматриваемые вопросы, чтобы обойти трудности, связанные со сложностью атомной структуры и атомных спектров. Сейчас мы сделаем несколько полезных замечаний для читателей, которые специализируются скорее в технике, чем в физике, чтобы указать им на некоторые проблемы, связанные с атомными переходами.

Сравнительно малое число коэффициентов A_nm и B_nm существенно отлично от нуля. Другими словами, обычно происходят только некоторые переходы, тогда как вероятность других переходов равна нулю или близка к нему. Правила, выделяющие разрешенные переходы, т. е. переходы, имеющие не нулевые вероятности, называются правилами отбора. Они выражаются через изменения квантовых чисел начального и конечного состояний. Одно из основных правил отбора, применимое к атомам и ионам с двумя активными электронами, запрещает переходы из синглетных состояний (два электрона с противоположно направленными спинами) в триплетные состояния (спины параллельны). Принимая во внимание некоторые правила отбора, полезно выделять энергетические уровни (синглетные, триплетные и т. д.) в отдельные столбцы и даже подразделять эти столбцы в дальнейшем на четные и нечетные состояния, поскольку разрешены переходы только из четных в нечетные и из нечетных в четные состояния. Если имеются три уровня А, В и С, разрешены переходы из А в В и из А в С, то вследствие правила четности запрещены переходы из В в С.

Однако природа не так строга, как математика, и на самом деле запрещенные переходы имеют место, но гораздо реже, чем разрешенные. Лучше подразумевать под запрещенными переходами такие переходы, вероятность которых на порядок величины меньше, чем вероятности переходов, разрешенных правилами отбора. Эти правила наиболее строго выполняются для элементов начала периодической таблицы. Они теряют свою силу в сложных атомах и при сильном взаимодействии одного атома с другим, что имеет место при столкновении или при взаимодействии в кристаллической решетке.

В результате правил отбора атом может попасть в возбужденное состояние, из которого ему будет трудно вернуться в основное состояние. Состояние, из которого все переходы в более низкие энергетические состояния запрещены, называется метастабильным; атом, попавший в такое состояние, как правило, будет оставаться в этом состоянии значительно дольше, чем это имеет место в обычном возбужденном состоянии, из которого легко перейти на более низкий уровень. Метастабильное состояние имеет большое время жизни.

Целью настоящего параграфа было введение понятий, используемых в обсуждении вынужденного излучения и в установлении основных соотношений между коэффициентом поглощения, сечением поглощения, населенностью атомных уровней и коэффициентами Эйнштейна. Мы также упомянули о некоторых правилах отбора без объяснения, каковы они на самом деле и как они связаны с квантовыми числами. Интересующийся читатель, который еще не знаком с этими вопросами, найдет в книге Митчелла и Земанского [62] полезный материал относительно поглощения и излучения. В книге Гернберга [32] содержится элементарное изложение правил отбора; для изучения теории следует обратиться к учебникам по квантовой механике, таким, например, как книги Кембла [46] и Полинга и Вильсона [67].