§ 2. Когерентность и некогерентность

До сих пор мы обсуждали только те свойства света, которые могут быть описаны через интенсивность. Будучи электромагнитным излучением, свет характеризуется не только интенсивностью, но поляризацией и фазой. Оставив пока в стороне поляризацию, мы будем исследовать проблемы, касающиеся фазы.

Очевидность существования фазы доказывается классическими интерференционными опытами, в которых демонстрируется, что амплитуды двух лучей от одного точечного источника после прохождения лучами различных расстояний должны складываться согласно известным правилам векторного сложения, причем направление складываемых векторов зависит от длины пройденных путей.

Общей характеристикой всех классических источников света является отсутствие когерентности между световыми волнами, испущенными из различных точек излучателя. Под термином "когерентность", или "пространственная когерентность", мы подразумеваем корреляцию фаз монохроматического излучения, испущенного из двух различных точек. Строго говоря, нам следовало бы говорить не о когерентности или некогерентности света, но о различных степенях корреляции, и таким же образом нам не следовало бы использовать термин "монохроматический" как не имеющий смысла, поскольку строго монохроматического излучения не существует. Однако практически мы можем рассматривать излучение, испущенное из двух отдельных источников, как некогерентное, если интенсивности излучения аддитивны. Мы принимаем как установленный экспериментальный факт, что свет, испущенный из двух точек обычного источника, расстояние между которыми больше длины волны излучения, не может давать интерференцию, даже если выделены предельно узкие "монохроматические" компоненты.

Из этого факта мы делаем вывод об отсутствии корреляции между фазами пространственно разделенных излучателей.

Другой стороной проблемы является когерентность во времени. При обычных условиях интерференция может наблюдаться при разделении света, испущенного из одной точки источника, и последующем сведении разделенных лучей в одной области после прохождения ими различных путей, если только длины этих путей отличаются не более чем на несколько сантиметров. Интерференция не наблюдается, если разность длин путей превосходит, скажем, 30 см, так как фаза излучения не сохраняется источником в течение времени прохождения светом этого расстояния. В идеальной монохроматической волне амплитуда колебаний в любой фиксированной точке постоянна, в то время как фаза меняется линейно со временем. Этот случай не имеет места в волне, создаваемой реальным источником; амплитуда и фаза испытывают хаотические флуктуации, скорость которых зависит от ширины спектра Δv. Временем когерентности является интервал времени Δt = 1/Δv. В течение временного интервала, значительно более короткого, чем Δt, излучение является почти монохроматической волной, что несправедливо для большего временного интервала.

Рассмотрим более подробно электромагнитное поле в двух точках P₁ и Р₂ в волне, созданной протяженным монохроматическим источником, который удален от точек Р₁ и Р₂ на расстояние, много большее длины волны. Если P₁ и Р₂ так близки друг к другу, что разность SP₁-SP₂ между путями из каждой точки источника S мала по сравнению с длиной волны λ, то можно ожидать, что флуктуации в P₁ и Р₂ фактически будут одинаковыми. Более того, можно ожидать, что некоторая корреляция будет существовать даже для больших расстояний между Р₁ и Р₂ при условии, что разность путей не превышает когерентной длины с Δt~c/Δv. Используя эту корреляцию электромагнитных возмущений, мы приходим к определению области когерентности вокруг любой точки электромагнитного поля волны, генерируемой монохроматическим источником.

Распространение понятия корреляции на немонохроматическое поле производится прямым способом, но с большими математическими ограничениями. Характеристики излучения должны быть представлены в виде интегралов Фурье и корреляции между составляющими компонентами должны быть определены таким же образом, как это делается в теории стационарных случайных процессов. Этот анализ был проведен [9] и был получен следующий результат: степень когерентности γ₁₂ (τ), абсолютное значение которой меняется от 0 до 1, может быть вычислена для заданных двух точек в данном интервале времени τ. Имея в виду это обстоятельство, можно обсудить изменение степени когерентности волны, испускаемой протяженным источником. Степень когерентности излучения между точками P₁ и Р₂ может быть связана с дифракционной картиной источника, рассматриваемого как отверстие, для которого имеется определенное распределение амплитуды и фазы. В этом заключается сущность теоремы Зиттера-Цернике [9], которая позволяет вычислить изменение γ(0) в плоскости, освещаемой протяженным некогерентным источником.

Идеальный случай γ(0) = 1 соответствует полностью когерентной плоской волне с волновым фронтом, совпадающим с плоскостью наблюдения. Этого, разумеется, нельзя достичь, используя любой некогерентный источник конечной протяженности. Степень когерентности |γ(0)| уменьшается при удалении точки Р₂ от фиксированной точки Р₁. Принято называть излучение "почти когерентным" в той области, где выполнено условие |γ|≥ 0,88. В математических выводах теоремы Зиттера-Цернике показано, что диаметр круга, освещенного почти когерентно от почти монохроматического, однородного, кругового, некогерентного источника с угловым радиусом α = ρ/R, равен d = 0,16λ/α. Здесь угловой радиус α определен с помощью радиуса источника ρ и расстояния Р от точки наблюдения до источника [9].

Важно помнить, что от некогерентного источника можно получить почти когерентный пучок конечного поперечного сечения, но при этом будет использована лишь малая часть излученной энергии. Чтобы получить почти когерентный пучок диаметром в 1 см на длине волны 5000 Å, источник должен быть с помощью оптической системы настолько удален, что его угловой радиус α будет равен 8*10^-6 рад. Если источник с площадью A и плотностью потока излучения w_s излучает свет согласно закону Ламберта, то плотность потока излучения на расстоянии R от излучателя в направлении, близком к нормали к поверхности, равна

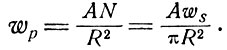
Следовательно, для излучателя, имеющего вид круга с радиусом ρ, имеем

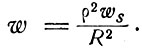
Чтобы получить когерентный пучок диаметром 1 см, мы должны иметь α = ρ/R = 0,16λ; следовательно, w_p = (0,16λ)²w_s = 0,64*10^-10w_s. В этом случае плотность потока излучения в почти когерентной части пучка в 10^-10 раз меньше плотности, излучаемой источником.

Почти когерентный пучок может быть сфокусирован в пятно с размерами порядка длины волны. Если получен почти когерентный пучок, то можно сконцентрировать его энергию, причем степень концентрации зависит от степени когерентности пучка.

Теперь мы можем оценить некоторые преимущества когерентного или почти когерентного источника, который дает излучение в виде сферической или плоской волны ограниченного поперечного сечения. Это излучение может быть сконцентрировано с помощью линз и зеркал в изображение, яркость которого больше яркости первоначального источника. Более того, испущенное источником излучение в виде почти плоской волны можно направить на удаленный объект с очень малыми дифракционными потерями, в то время как лишь малая часть излучения от некогерентного источника может быть преобразована в почти плоскую волну.