Глава IV. Лазеры на основе твердых веществ

§ 9. Рубиновый лазер Меймана

Как было сказано выше, в первом лазере, работающем на длине волны 6943 Å, использовался кристалл рубина. В течение двух лет после открытия Меймана были получены другие вещества, подходящие для лазеров, а кристалл рубина был использован в лазерах, работающих на других частотах. Тем не менее рубиновые лазеры лишь с небольшими изменениями по сравнению с первоначальным лазером все еще являются наиболее мощными источниками когерентного света.

В настоящей главе дается общее описание лазера и его технические характеристики, так как в предыдущих главах это описание было неполным и приводимый материал был необходим только для подтверждения математических выкладок.

В молодой и быстро развивающейся области физики, связанной с созданием и разработкой лазеров, численные значения их характеристик и достигнутые результаты меняются с каждым месяцем, так что приводимые данные отстают от тех, которые получены в лабораториях и известны работающим в этой области специалистам. Безусловно, некоторые данные, приводимые в этой книге, устареют к тому времени, когда они дойдут до читателя. Чтобы уменьшить неизбежное старение этой монографии, автор включил в настоящий раздел многие еще не опубликованные данные, за которые он признателен своему коллеге Баденхагену.

Основой лазера Меймана является кристалл розового рубина, который по химическому составу представляет собой Al₂O₃ с 0,05 весов. % Cr₂O₃. В явлении генерации света участвуют только ионы хрома, а алюминий и кислород остаются инертными. При такой концентрации плотность ионов хрома N₀ = 1,62*10¹⁹ см^-3. Кристалл имеет почти кубическую симметрию, искаженную вдоль одной из пространственных диагоналей. В результате такого искажения истинная симметрия кристалла рубина ромбоэдрическая. Элементом симметрии кристалла рубина является ось вращения третьего порядка, которая, естественно, совпадает с оптической осью кристалла (ось с).

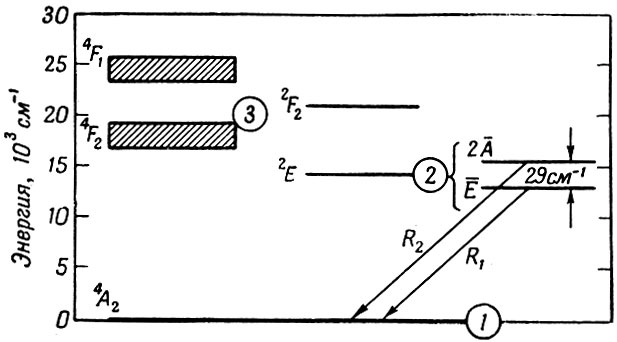
Фиг. 15. Диаграмма энергетических уровней для рубина с примесью хрома

Точная диаграмма энергетических уровней рубина без учета незначительного расщепления основного уровня изображена на фиг. 15. Обозначение этих уровней согласуется с теорией групп, т. е. эти обозначения связаны с волновыми функциями, описывающими электроны на этих уровнях. Важными особенностями энергетической диаграммы являются две широкие зоны поглощения ⁴F₁ и ⁴F₂ и расщепление уровня ²Е. Коэффициент поглощения света розовым рубином (см. фиг. 16) зависит от направления распространения света по отношению к оптической оси кристалла. Максимумы на кривых поглощения точно соответствуют центрам зон, энергетическая диаграмма которых изображена на фиг. 15. Флуоресценция рубина характеризуется линиями R₁ и R₂, но обычно лазер работает только на излучении, характеризуемом линией R₁ (6943 Å). Для света, распространяющегося вдоль оси с, коэффициент поглощения в максимуме для линии R₁ при комнатной температуре k₀ = 0,4 см^-1 и сечение поглощения σ₀ = 2,5*10^-20 см². Время жизни для перехода R₁ составляет 4,3 мсек при 77° К и 3,0 мсек при 300° К.

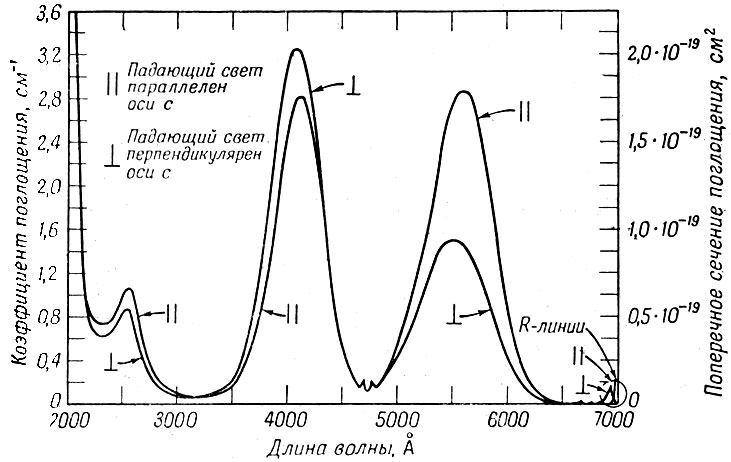
Фиг. 16. Спектр поглощения рубина

Цилиндрический образец рубина окружен витками спиральной импульсной лампы, как это показано на фиг. 3 и 4, однако возможно использование и других конструкций, обеспечивающих интенсивное облучение. Среди многих успешно используемых импульсных ламп имеются лампы GEFT-506 и GEFT-524, EGGFX-1 и EGGFX-38 и ряд других специально изготовленных ламп. Вспышка ламп осуществляется с помощью разряда конденсатора емкостью в 50 мкф или больше через газ, наполняющий лампу. Используются и большие, емкости до 2000 мкф. Разряд вызывается импульсным преобразователем, который обеспечивает пиковое напряжение для пробоя после того, как напряжение приложено к импульсной лампе. Напряжения обычно лежат в области от 1 до 2 кв, но иногда используются-напряжения более 4 кв. Высокие напряжения позволяют затрачивать на вспышку ту же энергию, но при меньшей емкости. Однако такие напряжения могут быть использованы только в лампах, которые не пробиваются при высоком напряжении в отсутствие стартового импульса, или с применением разделительного выключателя, такого, как игнитрон, последовательно соединенного с лампой. Если стоимость оборудования не имеет значения или если чрезвычайно важна форма импульса, то источником энергии для питания импульсной лампы может служить импульсный модулятор.

Размеры рубиновых стержней выбираются приблизительно между 0,1 и 2 см в диаметре и 2 и 23 см по длине. Концы цилиндров тщательно отполированы с параллельностью в пределах одной угловой минуты. Работа лазера улучшается с улучшением качества полировки поверхностей и их взаимной параллельности. Серебряное покрытие наносится так, что один конец рубина становится полностью отражающим; другой конец посеребрен не так плотно, и его коэффициент пропускания может составлять от 5 до 80 или 90%. Наиболее характерное значение коэффициента пропускания колеблется от 10 до 25%, исключение составляют очень длинные кристаллы. В некоторых случаях частичное пропускание достигается путем создания отверстия в полностью посеребренной поверхности. Частично прозрачные серебряные поверхности не свободны от потерь, следовательно, коэффициент отражения от таких покрытий на торцах кристалла редко превышает 85 или 90%. Когда необходимо получить больший коэффициент отражения, используются многослойные диэлектрические пленки. Коэффициент отражения входит в условие самовозбуждения (6.10) и в выражение для скорости установления генерации в рубине. Большой коэффициент отражения дает низкий порог возбуждения и высокую плотность излучения внутри рубина. Последнее обстоятельство приведет к увеличению потерь в лазере и уменьшению получаемой на выходе полной энергии. Оптимальная величина коэффициента отражения частично прозрачного конца зависит от длины кристалла лазера, от целей использования излучения лазера и от скорости, с которой подводится возбуждающая энергия.

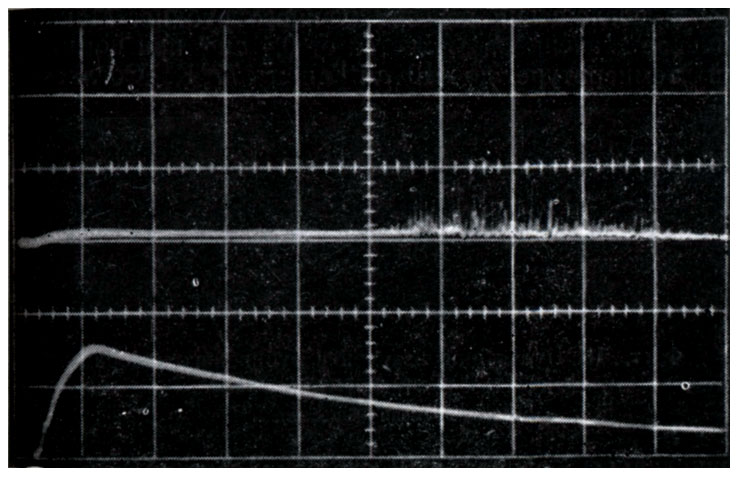
Фиг. 17. Зависимость интенсивности излучения рубинового лазера от времени. Верхняя линия - свет, испущенный рубином; нижняя - свет, испущенный импульсной лампой. Шкала времени - 0,1 мсек/см

На фиг. 17 приводится осциллограмма интенсивности выходящего из лазера излучения вместе с осциллограммой интенсивности возбуждающего излучения. Флуоресценция начинается немедленно после начала возбуждения, но вынужденное излучение начинается в этом случае приблизительно на 0,5 мсек позже. Острые маленькие пики интенсивности соответствуют быстрым пульсациям интенсивности вынужденного излучения. Они показаны в растянутой по времени шкале на фиг. 18.

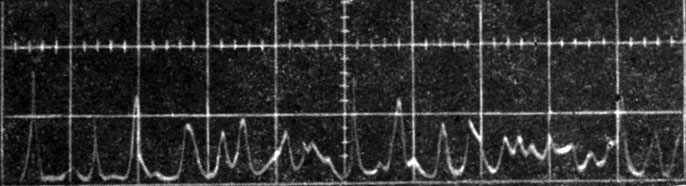
Фиг. 18. Пульсации излучения рубинового лазера в растянутой по времени шкале. Шкала времени - 5 мксек/см

Хаотичность этих пульсаций и очевидное отсутствие их повторяемости указывают на то, что они вызваны различными факторами^*. Одним из этих факторов является наличие взаимодействия между многими модами в резонаторе, в котором колебания возникают и затухают в различных модах с различными скоростями. Более важным является то, что возбуждение рубина в целом неоднородно; следовательно, вынужденное излучение развивается в каждой части кристалла с различной скоростью и не одновременно. Процесс возбуждения зависит от температуры кристалла, так как спектральная ширина линии, входящая в выражение для коэффициента усиления а, является функцией температуры. В § 6 было показано, что функция зависимости коэффициента а от частоты описывается колоколообразной кривой. Ширина этой кривой и значение а в ее максимуме зависят от температуры таким же образом, как и для k₀ - коэффициента поглощения невозбужденного рубина. Максимальное значение k₀ меняется от 0,4 см^-1 при комнатной температуре до 10 см^-1 при 77° K. Согласно вычислениям Хелворта [29], это изменение максимального значения коэффициента поглощения (усиления) может объяснить уменьшение порога самовозбуждения и изменение частоты пульсаций излучения, наблюдавшееся при температуре жидкого азота Коллинсом и др. [18]. Естественно, что частота пульсаций излучения зависит от всех параметров, которые входят в условия самовозбуждения, например от расстояния между зеркалами и от коэффициента отражения^**.

^* (При тщательно контролируемых условиях могут быть получены регулярные пульсации. См. § 10.)

^** (В работе [126] наблюдалась регулярная генерация при температуре -165° С.- Прим. ред.)

В случае рубинового лазера длина волны излучения, характеризуемого линией R₁, равна 6934 Å при 77° К, а при комнатной температуре -6943 Å. Согласно опубликованным данным Абеллы и Камминса [1], в области от 20 до 80° С температурная зависимость длины волны излучения однозначно аппроксимируется следующей формулой:

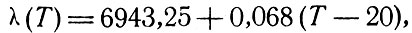
(9.1)

где Т измеряется по шкале Цельсия. Изменение длины волны с температурой объясняет некоторую неопределенность в ширине линии излучения лазера. Хотя длительность обычной лазерной вспышки порядка только миллисекунды, однако в течение этого периода кристалл сильно нагревается. Поэтому весьма вероятно, что наблюдаемая во многих случаях ширина линии в 0,1 Å по крайней мере отчасти является результатом частотного уширения за период наблюдения (см. § 8).

Поляризация лазерного излучения зависит от ориентации оптической оси рубина относительно оси стержня кристалла. Согласно измерениям Нелсона и Коллинса [65], поляризация полностью отсутствует, когда эти оси параллельны. Когда ось рубинового стержня образует с оптической осью угол в 60 или 90°, возникает 100-процентная линейная поляризация излучения, причем электрический вектор перпендикулярен плоскости, в которой лежит оптическая ось. Измерения Нелсона и Коллинса были продолжены в области температур от 100 до 300° К и подтвердили то, что ожидалось на основе поляризационных свойств флуоресценции, излучаемой рубином.

Когерентность света, обусловленная частичным отражением, и резкая направленность излучаемого пучка - явления тесно связанные. Направленность пучка обычно определяется распределением фазы и амплитуды в поперечном сечении пучка. Действительно, наиболее прямым доказательством появления вынужденного излучения в рубине является внезапное изменение в распределении направления распространения света, испускаемого при превышении порога самовозбуждения. Коллинс и др. [18] наблюдали это изменение в направленности на тщательно изготовленном рубиновом стержне диаметром 0,5 см, концы которого были параллельны с точностью до угла в 1 мин. Излучение флуоресценции было не направленным до тех пор, пока не был достигнут порог самовозбуждения; при достижении самовозбуждения появлялся луч, который отклонялся от оси образца на угол от 0,3 до 1°. Работая в режиме сильного превышения порога самовозбуждения, Баденхаген, Лендьел, Мак Кланг и Смит [14] получили от кристалла рубина диаметром 1 см луч с расходимостью 0,7°. Это соответствует углу конуса 0,35°, или 6 мрад. Фактически при тщательно контролируемых условиях расходимость пучка может быть снижена почти до 1 мрад. Эта расходимость значительно больше, чем следовало бы ожидать из теории дифракции, предполагая, что излучение из круглого пятна диаметром d происходит в фазе и с однородной амплитудой. Теория приводит к значению

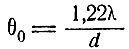
для углового расстояния первого нуля от центра дифракционной картины. Для d = 1 см и λ = 6943*10^-8 см получим θ₀ = 0,085 мрад. Объяснить наблюдаемую значительно большую расходимость можно, вероятно, тем, что не со всей площади поверхности излучение однородно по фазе и амплитуде.

Исследование фотографий поверхности рубина показывает, что распределение света не является однородным по всей поверхности. Коллинс, Нелсон и др. [18] впервые наблюдали изолированные светящиеся пятна на поверхности рубина, дающего вынужденное излучение. Позднее Евтухов и Ниленд [23] детально изучили распределение этих пятен, появляющихся на торцах рубина в различных экспериментальных условиях при возбуждении, слегка превышающем порог генерации. На кристаллах диаметром 2 и 3 мм отдельные пятна имели размеры порядка 100 мк, образованные ими комплексы достигали 850 мк. Оказывается, что расходимость пучков, испускаемых этими образцами, имеет значения, согласующиеся с расчетными, если за величину светящейся области принять размеры пятен. Евтухов и Ниленд измерили поляризацию света, излучаемого различными комплексами, и попытались связать появление комплексов пятен с различными другими характеристиками лазера, такими, как временная зависимость выходящего светового импульса и частота излучения. Была сделана попытка установить связь между некоторыми комплексами пятен и различными модами резонатора. Кроме аксиальных мод, в рубине могут иметь место и другие моды, особенно когда отношение длины к диаметру лазера невелико. Это можно предположить вследствие того, что при прочих равных условиях кристаллы с большими расстояниями между зеркалами дают более узкие пучки.

Прямое исследование когерентности с помощью экспериментов по интерференции подтвердило ожидаемые эффекты. Коллинс и его сотрудники [18, 66] провели эксперименты по дифракции от прямоугольного отверстия размером 50×150 мк, сделанного на одном из отражающих покрытий, и исследования интерференции от двух длинных параллельных щелей шириной 7,5 мк, разделенных расстоянием в 54,1 мк и расположенных также на одной из отражающих поверхностей. Эти исследования показали, что области на отражающей поверхности, участвующие в когерентной генерации, имеют диаметр порядка 0,05 см, что хорошо согласуется с наименьшей расходимостью пучка, полученного от этих лазеров.

Максимальное значение излученной мощности лазера с нерегулируемой интенсивностью импульсов является несколько неопределенной величиной, так как пики интенсивности, как это показано на фиг. 17 и 18, хаотичны. При благоприятных условиях от лазеров с кристаллами диаметром 1 см и длиной 4 см была получена максимальная мощность от 20 до 30 квт. Среднее значение мощности за вспышку длительностью 1 или 2 мсек значительно меньше. Более важна и гораздо легче измерима полная энергия излучения за одну вспышку. Эта энергия зависит от возбуждения и размера рубина; величина от 0,1 до 1,5 дж является весьма типичной для лазеров с кристаллами диаметром около 1 см и длиной 4 см. Конечно, многое зависит от способа возбуждения, качества рубина, качества и расположения зеркал.

Коэффициент полезного действия лазера определяется как отношение когерентно испущенной энергии к электрической энергии, затраченной в импульсной лампе, и является функцией многих параметров. К наиболее важным параметрам относятся спектральные характеристики импульсной лампы, которые в свою очередь зависят от состава и давления газа в лампе. Наиболее эффективной оказалась ксеноновая лампа при давлении 150 мм рт. ст. (см. § 1 и 5). В обычных лазерах, использующих кристаллы рубина диаметром 1 см и длиной 4 см, как правило, используются лампы с энергией вспышки от 500 до 1000 дж. Кузиканани с сотр. [49] выполнил точные измерения зависимости энергии излучения рубинового лазера (длина кристалла 6,25 см, диаметр 0,625 см) от энергии, затраченной на вспышку лампы, при использовании импульсной лампы FGGFX-38. Была обнаружена линейная зависимость, изображенная на фиг. 19. По-видимому, энергия излучения исследованного лазера увеличивается линейно с ростом электрической энергии, затраченной на вспышку лампы, с коэффициентом пропорциональности 0,0006. Эти измерения были выполнены с рубином при комнатной температуре, причем не выбирались специально оптимальные условия, ведущие к высокой энергии выхода. Наблюдалось увеличение к. п. д. при температуре жидкого азота.

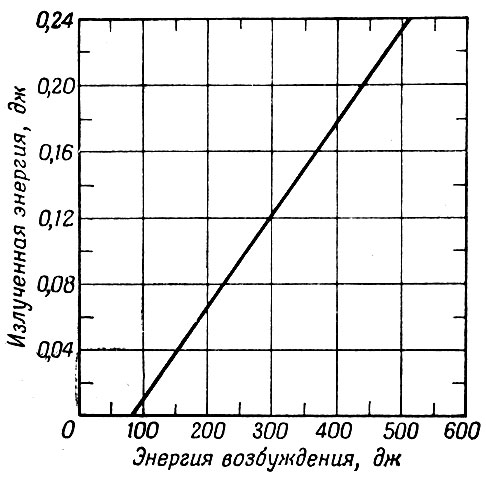
Фиг. 19. Зависимость энергии выхода от затраченной электрической энергии

С охлажденными кристаллами рубинов, по-видимому, можно достичь увеличения к. п. д. в четыре раза по сравнению с измеренным Кузиканани.

Следует иметь в виду, что для работы лазера к единице объема рубина должна подводиться некоторая определенная минимальная энергия, и она должна подводиться со скоростью, превышающей некоторую минимальную скорость, которая достаточна для перекрытия потерь, связанных со спонтанным затуханием. Эта "минимальная" скорость, как мы уже заметили, настолько велика, что может быть обеспечена только наиболее мощными лампами. Конечно, поглощаемая в рубине энергия является только малой частью полной энергий излучения импульсной лампы, так как значительная доля этого излучения не будет полезно поглощаться рубином. В возбуждении эффективно участвует только излучение в соответствующей области поглощения, характеризуемой кривой на фиг. 16.

Наиболее сложные технические проблемы, связанные с созданием лазера, заключаются в концентрации имеющегося возбуждающего излучения на кристалле рубина и в эффективном удалении той подавляющей Доли падающей энергии, которая преобразуется в тепло.