§ 8. Проблема спектральной ширины генерируемого излучения

(Этот параграф был написан по материалам Р. Хелворта.)

Генерируемое лазером излучение по существу является значительно усиленным шумом. Аналогичное явление имеет место во многих обычных классических генераторах. В таком генераторе шумы определяются тепловыми флуктуациями, их энергия равномерно распределена в широкой полосе частот, которая включает полосу усиления усилителя. В случае же лазеров шумы определяются спонтанным излучением, характеризуемым центральной частотой и шириной излучаемой спектральной линии. В любом случае усиление регенеративно, т. е. часть излучаемой энергии возвращается обратно в систему. Следовательно, частота, соответствующая максимальному усилению, будет доминировать в излучении. При определенных условиях усилитель может иметь несколько максимумов усиления, лежащих при различных частотах.

Рассмотрим пакет фотонов различной частоты, испущенных спонтанно внутри активного вещества лазера. Этот пакет характеризуется частотным распределением, присущим спектру спонтанного излучения атома, т. е. центральной частотой v_a и шириной линии Δа. Как было объяснено в § 6, после m прохождений через активное вещество лазера пакет фотонов будет усилен в r^m exp [mα(v)L] раз. С увеличением m экспоненциальный множитель стремится сузить спектральное распределение около одной частоты, которая соответствует максимальному усилению. Этот процесс был бы тривиален, если бы имелась возможность аддитивного увеличения интенсивности и если бы величина r не зависела от частоты. Из того факта, что амплитуды света должны складываться, следует, что усиление света будет иметь место только в том случае, если свет, возвращаясь обратно в ту же точку, из которой он был испущен, имеет соответствующую фазу. Выполнение данного условия зависит от размеров лазера, выраженных в длинах волн излучаемого света. Очевидно, что здесь мы встретимся с проблемой возбуждения колебаний внутри резонатора при учете селективности усиления. Эта проблема известна читателям, знакомым с работой мазера на аммиаке. Новой особенностью этой проблемы в случае лазеров является наличие большого числа мод резонатора, соответствующих малому интервалу значений волнового вектора. Например, в § 7 мы получили, что в рубиновом кристалле длиной 10 см только аксиальные моды разделены друг от друга на 0,0284 см^-1 и между ними имеется еще большое число неаксиальных мод. Напротив, в случае мазера на аммиаке в резонаторе имеется только одна мода.

В среде с умеренными потерями различные моды резонатора могут быть представлены как независимые осцилляторы, каждый из которых характеризуется своей резонансной частотой и шириной спектральной линии излучения или добротностью Q. В лазерах мы обычно встречаемся с общей проблемой взаимодействия атомов, которые излучают и усиливают свет, со всеми соответствующими модами резонатора. Здесь мы не будем пытаться решить эту общую проблему, а схематично обсудим взаимодействие с одной модой резонатора, выбранной таким образом, что ее частота приблизительно совпадает с частотой, соответствующей максимуму излучения атома. В противоположность мазеру на аммиаке ширина атомной линии излучения в лазерах больше, чем разность между соседними, тесно расположенными частотами мод резонатора, так что вблизи максимума спектральной линии излучения атома располагается большое число резонансных частот резонатора. Предположим, что взаимодействие между модами отсутствует, и вычислим ширину линии излучения при условии возбуждения только одной моды.

Хотя предположение об отсутствии взаимодействия между модами не является полностью справедливым, все же это упрощение позволяет получить реальную оценку для спектра излучения. Эта оценка впервые была сделана Шавловом и Таунсом [75] в 1958 г. путем модификации соответствующего расчета для мазера на аммиаке. Она дала чрезвычайно узкий спектральный состав излучения и стимулировала попытки экспериментального осуществления лазера в оптической области. Модификация первоначальных расчетов Гордона, Цайгера и Таунса [28], связанных с работой мазера на аммиаке, состояла в замене неравенств hv<<kT и Δ_рез>>Δ_акт на обратные, причем Δ_рез и Δ_акт означают соответственно ширину линии резонатора и активного вещества.

Вопрос о спектральной ширине линии излучения тесно связан с теорией шумов и излучаемой мощностью, так как мы наблюдаем распределение излучаемой энергии в зависимости от частоты света. Источником первоначального сигнала является спонтанное излучение, подчиняющееся статистическим законам, так что нам известно его энергетическое распределение в зависимости от частоты излучения. При математическом анализе таких проблем необходимо осуществить переход от временной переменной к переменной по частоте и обратно. При таких преобразованиях принято использовать в качестве переменной угловую частоту ω = 2πv. Тогда осциллятор, который описывает данный резонатор, имеет частоту ω₀ и ширину линии Δ₀. Эти величины и величина добротности резонатора Q связаны соотношением ω₀ = QΔ₀. Пусть максимум излучения атома имеет место также при угловой частоте ω₀ и пусть ширина атомной линии излучения Δ_а значительно больше Δ₀^*. Собственные колебания осциллятора, характеризующего резонатор, описываются координатой q, которая может быть мгновенным значением напряженности электрического поля. Эта координата удовлетворяет дифференциальному уравнению

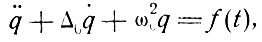
(8.1)

где f(t) - вынуждающая сила.

^* (Эта ширина линии равна 2πΔv.)

Второй член в левой части (8.1) характеризует диссипацию энергии. Известно, что осциллятор диссипирует энергию со скоростью

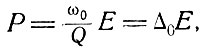
(8.2)

где Е - энергия осциллятора [см. (7.19)]. Могут иметь место несколько процессов, вызывающих диссипацию энергии при колебаниях в резонаторе. Один процесс может быть вызван диссипацией, связанной с веществом внутри резонатора, другой - с выходом энергии наружу через различные отверстия. Когда несколько независимых процессов диссипации энергии происходят одновременно, причем с каждым процессом связана диссипируемая мощность P_i и ширина Δ_i, то

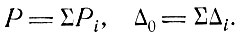
(8.3)

Следовательно, мощность, диссипируемая через i-й канал, равна

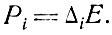
(8.4)

В стационарном режиме энергия определяется шириной линии Δ₀ и зависимостью спектральной плотности возбуждающей силы от частоты. Известно, что если возбуждающая сила имеет однородную спектральную плотность |F(ω)|² внутри ширины линии, то средняя энергия осцилляторов в стационарном режиме приблизительно равна

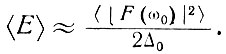
(8.5)

Угловые скобки означают статистическое усреднение по совокупности осцилляторов. Уравнение (8.5) получено обычным образом на основании того факта, что в стационарном режиме для осциллятора при действии периодической силы имеет место выражение

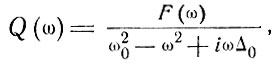
(8.6)

где Q(ω) и F(ω) - коэффициенты Фурье соответственно функций q(t) и f(t). Средняя энергия определяется интегрированием величины <(|Q(ω)|>²> по всем частотам. Практически существенна только область вблизи тех двух частот, где знаменатель правой части (8.6) велик, т. е. вблизи ω = ± ω₀.

В нашу задачу входит определение статистического среднего от |F(ω₀)|², когда вынуждающая сила является результатом спонтанного излучения атомов, излучающих независимо друг от друга. Рассмотрим колебания в резонаторе, содержащем поглощающее вещество при температуре Т. Известно, что средняя энергия осциллятора с большим значением Q, находящегося в тепловом равновесии при температуре Т, определяется формулой Планка

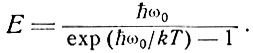
(8.7)

Предположим, что поглощающее вещество состоит из двух уровневых квантовых систем, энергетическое расстояние между которыми ћω имеет довольно широкое размытие вблизи ћω₀. При термодинамическом равновесии заполнение этих уровней подчиняется уравнению Больцмана (3.8). Тогда в простейшем случае равной кратности уровней имеем

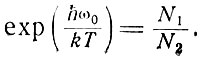
(8.8)

Следовательно, для осциллятора, находящегося в тепловом равновесии с совокупностью двухуровневых систем, выражение (8.7) приводится к виду

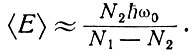
(8.9)

Из соотношений (8.5) и (8.9) получаем для вынуждающей силы, обусловленной шумами и связанной с двухуровневой системой, выражение

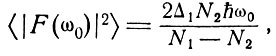
(8.10)

где Δ₁ - вклад в полную ширину линии от всех двухуровневых систем. В теории мазеров показано, что выражение (8.10) дает правильно усредненную спектральную плотность вынуждающей силы, даже когда N₂>N₁ и Δ₁<0. В этом случае мы имеем усиление вместо потерь, сужение линии - вместо уширения.

Вернемся к генерации с помощью лазера. В этом случае затухание обусловлено выходом излучения наружу. Характеристическими величинами являются излучаемая лазером мощность P_L и соответствующее затухание, характеризующееся величиной Δ₂. Совокупность атомов обеспечивает отрицательное значение Δ₁, так что член, описывающий полное затухание, или ширина линии, есть

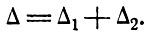
(8.11)

Тогда, согласно (8.4) и (8.5), средняя излучаемая мощность равна

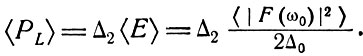
(8.12)

Принимая во внимание выражение (8.10), получаем

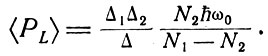
(8.13)

Опустим скобки при обозначении излучаемой мощности Р_L и отметим, что Δ является суммой положительных и отрицательных членов, которые почти равны на пороге генерации, так как в этом случае потери скомпенсированы усилением. Приближенно в числителе примем -Δ₁ ≈ Δ₂ и заменим Δ₂ символом Δ_c, чтобы подчеркнуть, что это ширина линии, характеризующая затухание в резонаторе, вызванное в основном выходом излучения наружу. Тогда

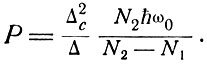
(8.14)

Следовательно, окончательная формула для зависимости ширины линии от угловой частоты имеет вид

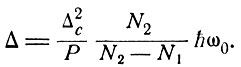
(8.15)

Шавлов и Таунс [75] вывели это соотношение для особого случая N₁ = 0 в терминах полуширины линий при значении мощности, равной половине максимального значения. Соответствующие переменные связаны с нашими следующими соотношениями:

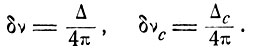
Следовательно, в обозначениях Шавлова и Таунса

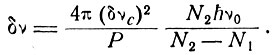
(8.16)

Повторим, что мы исследовали особый случай, в котором центр резонансной линии, характеризующей резонатор, совпадает с центром более широкой атомной спектральной линии. В том случае, когда это условие не является строго выполненным, выражения (8.15) и (8.16) все еще приближенно применимы, частота колебаний моды резонатора сдвинута к центру атомной спектральной линии, как это описано в § 7 [см. (7.20), (7.21)]. В § 7 было также качественно рассмотрено взаимодействие различных мод резонатора вблизи максимума спектральной линии излучения атома. Для более подробного исследования этого вопроса мы отсылаем читателя к работе Вагнера и Бирнбаума [83].

Во всех экспериментах, кроме специально поставленных, измерялась не ширина линии, определяемая выражениями (8.15) или (8.16), а эмпирическая ширина линии, которая является результатом одновременного наблюдения многих неразрешаемых линий. По этой причине разные эксперименты, проведенные на лазерах с кристаллами рубина, давали ширину излучаемой линии порядка 0,1 Å, которая, строго говоря, была обусловлена техникой измерений и не имела реального физического смысла. Реальная ширина линии значительно уже и зависит от уровня излучаемой мощности. Наиболее подходящее сравнение с формулой (8.15) может быть сделано при использовании данных Джавана для лазера, использующего смесь газов He - Ne (§ 17). Джаван смог наблюдать биение частот, получаемых от смешивания излучения двух различных мод лазера, и обнаружил, что частота биения имеет спектральную ширину около 2 гц. Следовательно, спектральная ширина линии излучения каждой моды лазера составляет 1 гц. Пусть излучаемая этим генератором мощность составляет 10^-3 вт (10⁴ эрг/сек). Ширина линии резонатора Δ_с, связанная с выходом излучения наружу, равна примерно ^с(1-r)/_L. Следовательно, для лазера длиной 100 см при отражении, равном 98%,

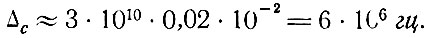
При частоте излучения лазера Джавана hv = 1,72*10^-12 эрг^*. Согласно эксперименту, отношение N₂/(N₂ - N₁) велико (между 10 и 100). Взяв нижнюю оценку для N₂/(N₂ - N₁), получим

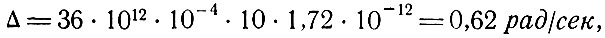
что соответствует ширине линии 0,01 гц.

^* (См. табл. 3 в конце книги.)

В заключение подчеркнем, что проблема ширины линии излучения лазера довольно сложна. Мы обсудили только простейшие случаи. Однако очевидно, что проблема ширины спектральной линии излучения лазера должна быть тщательно обсуждена, прежде чем может быть получен даже приближенный ответ.