§ 7. Возможные моды резонатора и выходящее излучение

(Всюду в дальнейшем различные типы колебаний электромагнитного поля называются модами, что соответствует общепринятой терминологии и сокращает длинное выражение.- Прим. перев.)

Основная часть лазера содержит совокупность усиливающих излучение атомов, помещенных между двумя частично отражающими зеркалами, которые заставляют излучение распространяться через усиливающую свет среду то в одном, то в другом направлении. В настоящем параграфе мы рассмотрим характер электромагнитного поля, возникающего внутри резонатора лазера, и свойства электромагнитного поля, выходящего из лазера.

Мы начнем рассмотрение с помощью простой теории, в которой предполагается существование однородных плоских волн конечного размера. Тогда в случае двух плоско-параллельных зеркал конечных размеров поле между этими зеркалами может быть представлено как суперпозиция полей плоских волн, распространяющихся в прямом и обратном направлениях. Не строго аксиальные плоские волны в этом случае рассеиваются, а аксиальные плоские волны образуют стоячую волну, которая становится устойчивой, если расстояние между зеркалами равно целому числу полуволн.

Устойчивость существенна для обеспечения генерации, следовательно, лазер будет генерировать излучение только на таких частотах, для которых выполнено условие

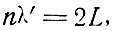
(7.1)

где n - целое число, 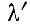- длина волны излучения внутри активного вещества лазера и L - расстояние между зеркалами.

Принято использовать символ λ для обозначения длины волны в вакууме. Следовательно, λ = c/v, тогда как 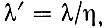где η - показатель преломления вещества.

В случае лазера, использующего кристалл рубина длиной в несколько сантиметров, число n порядка сотен тысяч. Каждое значение n соответствует частоте, на которой может иметь место генерация, при условии достаточного усиления на этой частоте. Определенное значение n характеризует определенный тип колебания, или моду. Строго говоря, должны рассматриваться две моды для каждой допустимой частоты вследствие возможных различий в поляризации.

Из уравнения

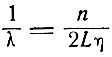
(7.2)

мы находим, что волновые векторы двух соседних мод отличаются на величину

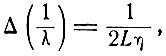
(7.3)

и отношение разности длин волн двух соседних мод к длине волны излучения равно

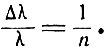
(7.4)

Эти соседние моды расположены так близко друг к другу, что многие из них находятся внутри одной атомной линии. Другими словами, частотная ширина полосы усиления, созданная совокупностью атомов, обычно включает несколько генерируемых мод. Теория, в которой используется представление о плоской однородной волне, точно предсказывает расстояние между частотами основных линий, для которых имеет место резонанс. Однако могут иметь место резонансы и для других волн. Более того, предположение об однородных плоских волнах конечных размеров несовместимо с принципами электромагнитного излучения. Наблюдение испускаемого лазером излучения является доказательством того, что поверхность зеркал не имеет одинаковую фазу и амплитуду на поверхности. Следовательно, необходимо дальнейшее уточнение теории.

Основная часть лазера, использующего твердые тела (например, кристаллы рубина) в качестве рабочего материала, во многих отношениях напоминает металлический резонатор с отверстием для выходящего наружу излучения. Наибольший интерес представляет излучение, распространяющееся точно в продольном направлении или вблизи него. Полезно также, хотя это и не совсем точно, представлять картину при помощи рассмотрения распространения лучей и принять, что излучение, распространяющееся под большими углами к продольным осям кристалла лазера, встречается с поверхностью до того, как усиление внутри кристалла может превысить неизбежные потери на поверхности. Следовательно, при отклонениях на большие углы от аксиального направления вынужденное излучение будет ничтожным. Для аксиального направления лучи испытывают полное отражение от отполированных сторон поверхности, следовательно, имеет место такой же результат, как если бы эти стороны были металлическими. Поверхность одного конца обычно является полностью отражающей, а поверхность другого конца - почти полностью отражающей. Следовательно, для описания мод вынужденного излучения можно рассматривать проводящий резонатор и считать выходящее наружу излучение возмущением для поля внутри резонатора.

Легко показать, что вектор-потенциал в прямоугольном резонаторе представляет собой сумму членов вида

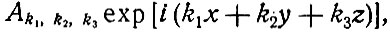
(7.5)

где

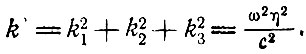
(7.6)

Граничные условия следующие:

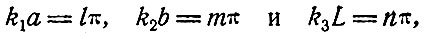
где a, b и L - размеры прямоугольного параллелепипеда, а l, m и n - целые числа. Тогда резонансные частоты определяются из уравнения

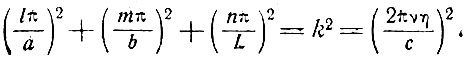
(7.7)

Для образца, имеющего форму цилиндра радиуса r, выражение (7.5) заменяется цилиндрическими функциями и уравнение (7.7) принимает вид

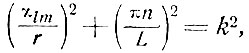
(7.8)

где χ_lm - корень функции Бесселя порядка l. Продольные или аксиальные моды в любом случае получаются при l = 0 и m = 0 приравниванием нулю величины χ₀₀. Тогда получаем уравнение (7.2). Другими словами, теория резонатора дает все моды простой теории и дополнительно поперечные моды, для которых l² + m² ≠ 0. В случае цилиндра первой поперечной моде соответствует l = 0, m = 1. Вычислим разность волновых векторов первой поперечной моды и аксиальной моды для большого значения n, обозначив через k₁ и k₀ волновые векторы поперечной и продольной мод соответственно. Тогда из уравнения (7.8) следует, что

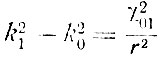
(7.9)

и соответствующая относительная разность частот равна

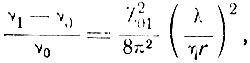
(7.10)

где λ - средняя длина волны, χ₀₁ = 2,405 соответствует первому нулю функции Бесселя J₀. Для рубинового стержня диаметром 1 см величина, стоящая в правой части (7.10), равна 4,56*10^-10.

В действительности же кристалл лазера представляет собой диэлектрический, не металлический резонатор, и точная теория в этом случае приводит к более сложной конфигурации поля внутри цилиндрического образца, чем та, которая была получена в предположении о металлических стенках резонатора [96]. Например, найдено, что поперечные электрические и поперечные магнитные поля существуют только для аксиально симметричных мод. Однако уравнение, определяющее резонансные частоты, имеет вид

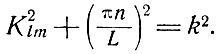
(7.11)

В то время как в случае цилиндрического резонатора, окруженного металлическими стенками, величины K_lm определяются решением уравнений

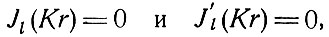
уравнения для K в случае диэлектрического резонатора более сложны и приводят к значениям K, которые в случае аппроксимации совпадают со значениями, полученными из упрощенного рассмотрения. Однако для почти аксиальных мод лазера число п очень велико, так что второй член доминирует в (7.11), и не слишком большая ошибка в величине K не меняет существенно значение частоты. В тех же случаях, когда рассматривается разность частот различных мод, следует использовать точное значение величин.

В теории электромагнитных волн показано, что обсуждаемые выше моды резонатора ортогональны друг к другу. Физически это означает, что колебания одной моды могут быть возбуждены без возбуждения других мод. Однако такая независимость мод справедлива только в идеальном случае, когда стенки резонатора обладают бесконечной проводимостью и имеют точную предполагаемую геометрическую форму. Отклонения от этих идеальных условий или учет поляризуемости вещества внутри резонатора могут привести к взаимодействию между модами, т. е. к передаче энергии колебаний от одной моды к другим.

Рассмотренная теория резонаторов хорошо описывает явления в лазерах, использующих в качестве активного вещества кристаллы, особенно в случае больших значений показателя преломления кристалла. Однако эта теория неприменима к лазерам, использующим газы, которые являются открытыми системами, имеющими два плоских или кривых зеркала на концах усиливающего газового столба. В типичном случае два плоских круглых зеркала диаметром 2 см устанавливаются на расстоянии 1 м друг от друга. В такой установке дифракционные потери не являются ничтожными; в действительности они могут стать важным фактором, определяющим распределение энергии внутри интерферометра при генерации. Если происходит генерация, то полная мощность, теряемая за счет рассеяния, дифракции и неполного отражения на зеркалах, должна быть уравновешена увеличением мощности при прохождении через активное вещество. В случае невзаимодействующих, или ортогональных, мод условие самовозбуждения должно быть выполнено для каждой генерируемой моды.

Система из двух параллельных зеркал известна в классической оптике как интерферометр Фабри - Перо. Когда этот интерферометр работает как пассивное устройство с однородными плоскими волнами, непрерывно вводимыми извне, поля внутри могут быть такими, какие имеются в плоской однородной волне. В случае же лазера, однако, мощность поддерживается только внутри интерферометра, потеря мощности на "краях" волны за счет дифракции будет заметно нарушать однородность.

Что же тогда подразумевать под модами интерферометра Фабри - Перо? Эти моды могут определяться и рассматриваться в зависимости от конфигурации поля на поверхности зеркал. Конфигурация поля называется поперечной модой, если после прохождения расстояния от одного зеркала до другого и возвращения назад поле волны имеет ту же фазу и амплитуду; т. е. функция, описывающая комплексную амплитуду на поверхности зеркала, умножается на определенное комплексное число, которое дает полный сдвиг фазы и потерю в результате одного прохождения до другого зеркала и обратно. Для каждой такой поперечной моды существует последовательность продольных мод, для которых фазовый сдвиг в результате такого замкнутого пути равен 2π. Обозначения и общая характеристика простейших мод, создаваемых плоскими круглыми и квадратными зеркалами, представлены на фиг. 9.

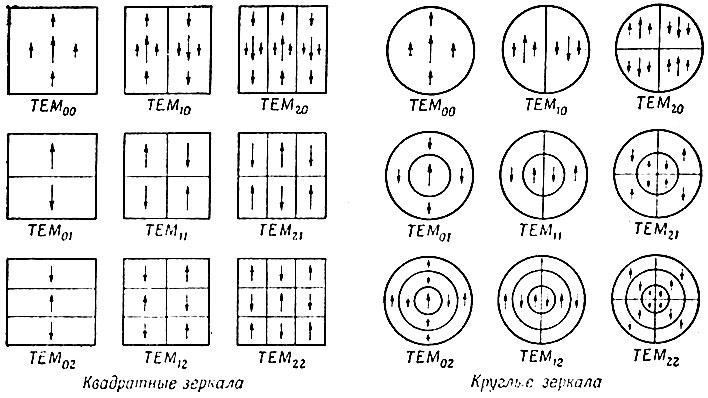
Фиг. 9. Конфигурация электрического поля для интерферометров с плоскими зеркалами

Моды интерферометра Фабри - Перо называются ТЕМ-модами, чтобы показать, что электрические и магнитные поля в большинстве случаев перпендикулярны продольной оси интерферометра. Эти моды имеют сходство с однородными плоскими волнами, которые являются строго поперечными электромагнитными волнами.

Фокс и Ли [24] вычислили ряд мод интерферометра Фабри - Перо для различных зеркал^*. Их расчеты базируются на обычной дифракционной формуле физической оптики, которая дает распределение поля в точке наблюдения в зависимости от распределения фазы и амплитуды в заданном поперечном сечении пучка. При расчете Фокс и Ли брали однородное распределение амплитуды и фазы на поверхности одного зеркала и вычисляли распределение амплитуды и фазы на поверхности другого. Полученная функция использовалась для следующего вычисления. Таким образом, получаются две последовательности распределений амплитуд и фаз, которые при известных обстоятельствах сходятся к самовоспроизводимым распределениям амплитуды и фазы. (В этих расчетах должно быть допущено однородное уменьшение амплитуды в одно и то же число раз, если учесть неизбежные потери.)

^* (В работе [125] при теоретическом рассмотрении дифракции на открытом конце волновода получены простые и наглядные соотношения для собственных колебаний открытых резонаторов. в аналитическом виде.- Прим. ред.)

Эти самовоспроизводимые фаза и относительное распределение амплитуды вдоль поперечного сечения могут характеризовать основную резонансную моду интерферометра. Конфигурация фазы и амплитуды является функцией параметра N = a²/λL, где а - радиус круглых зеркал и L - расстояние между ними.

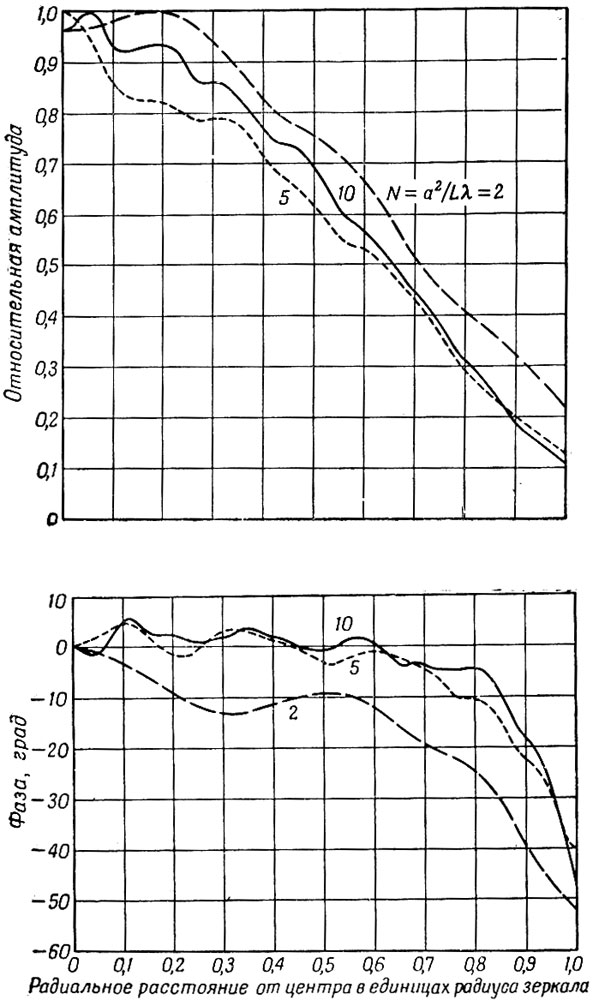
Фиг. 10. Распределение относительной амплитуды и фазы основной (ТЕМ₀₀) моды для плоских круглых зеркал

Пример распределений, полученных Фоксом и Ли, изображен на фиг. 10, где для N = 2, 5, 10 представлена основная (ТЕМ₀₀) мода для двух плоских круглых зеркал. Немонотонность кривых связана с различными зонами Френеля. Фокс и Ли также получили интересные несимметричные распределения для некоторых геометрий в результате расчета дифракционных потерь, связанных с их модами как функции от числа N.

На фиг. 11 воспроизведены данные Фокса и Ли, полученные в случае дифракционных потерь для интерферометра с плоскими круглыми зеркалами. Из этих данных следует, что потери за счет дифракции при одном прохождении для моды ТЕМ составляют 0,9% для N = 10, т. е. составляют величину, сравнимую с обычными потерями для газовых лазеров, вызванными неполным отражением. При экстраполяции до значения N = 50, которое вполне реально для созданного Джаваном лазера, использующего смесь гелия и неона, дифракционные потери уменьшаются до 0,09% и становятся малыми по сравнению с потерями при отражениях. Отметим, что учет распределения фазы и амплитуды на поверхности зеркал ведет к уменьшению дифракционных потерь по сравнению с тем случаем, когда это распределение однородно.

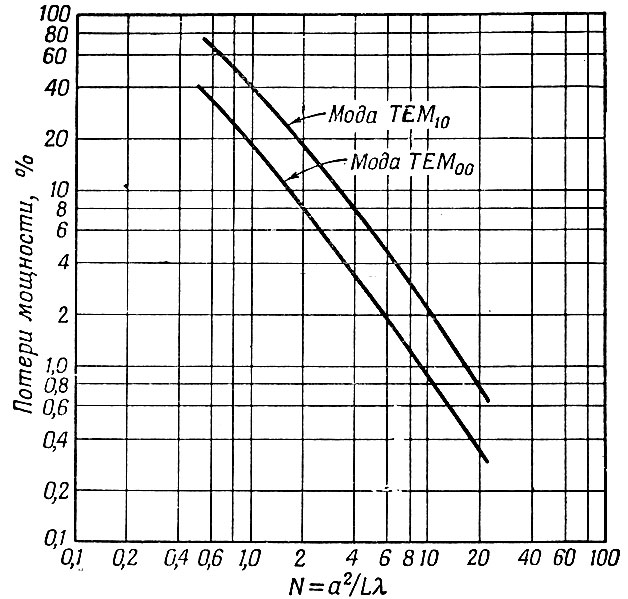
Фиг. 11. Дифракционные потери при одном прохождении в зависимости от N = a²/λL для плоских круглых зеркал

Интересно рассмотреть изменение дифракционных потерь для различных мод, так как если между модами не существует различия в потерях, то лазер, в котором перевыполнены условия самовозбуждения, будет одновременно генерировать несколько мод. Хотя потери, связанные с неполным отражением от зеркал, могут быть больше дифракционных потерь, они являются одинаковыми для всех мод, следовательно, различие в суммарных потерях между модами в основном связано с различием в дифракционных потерях. Как известно, условие самовозбуждения включает полное усиление вдоль пути и сумму всех потерь при прямом и обратном прохождении. Котик и Нью-штейн [51] отметили, что для интерферометра Фабри - Перо, имеющего неограниченные размеры зеркал (это приближение соответствует плоской волне), наклонная мода возбуждается прежде, чем аксиальная, что связано с тем, что наклонный луч проходит, усиливаясь, больший путь, чем аксиальный луч, а потери для мод совершенно идентичны. Они нашли условие для минимальной мощности, необходимой для возбуждения аксиальной моды. Это условие ограничивает максимальные поперечные размеры зеркал в зависимости от расстояния между зеркалами, коэффициента отражения и длины волны. Во всех физически приемлемых случаях это условие выполнено.

Фокс и Ли [24] получили результаты с помощью большой серии численных расчетов, включающих около 300 итераций, или преобразований амплитуд. Проблема может быть сведена к интегральному уравнению, собственные значения которого дают долю потерь (дифракционных) на одно прохождение и решением которого является самовоспроизводимое комплексное распределение амплитуды. Танг [97] получил в этой формулировке вариационное решение для случая бесконечных плоских зеркал, имеющих форму полос. Для практически более важных круглых зеркал получены только грубые оценки с помощью математических расчетов.

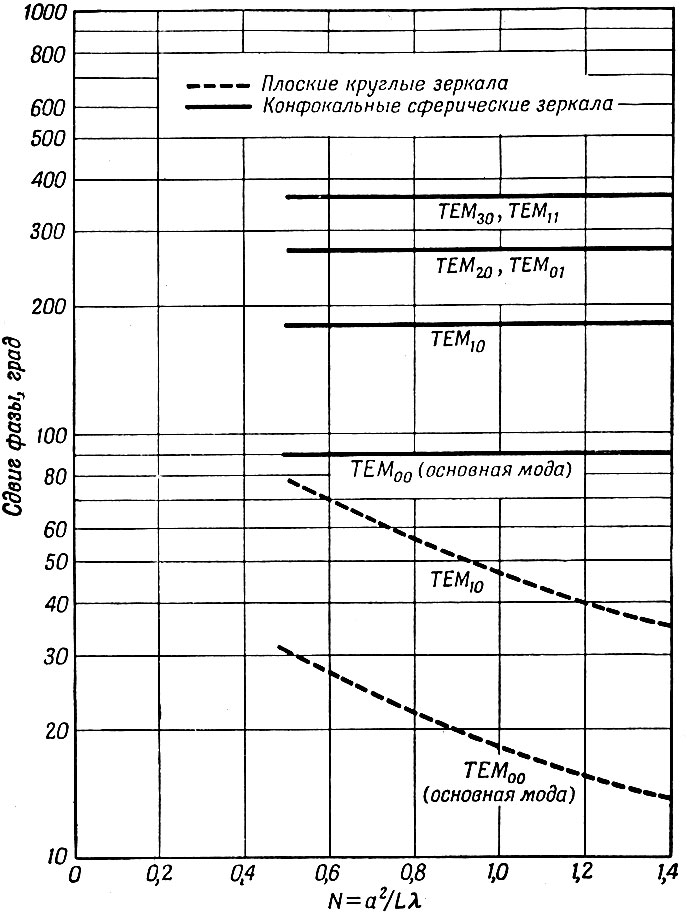
Фиг. 12. Фазовый сдвиг при одном прохождении (отнесенный к геометрическому фазовому сдвигу) в зависимости от N = a²/λL для конфокальных сферических зеркал. Пунктирные кривые для плоских круглых зеркал приведены для сравнения.

В связи с проблемой газовых лазеров особый интерес приобретает разделение различных мод по частоте, так как это разделение связано с чрезвычайно высокой степенью разрешения. При вычислении разности частот между модами мы должны учитывать моды, полученные Фоксом и Ли, а не те, которые были получены в результате расчета резонатора [(7.9) и (7.10)]. Из теории волновода известно о том, что фазовую скорость мод интерферометра нельзя полагать равной скорости света. Скорее следует ожидать, что эта скорость приближается к скорости света при больших значениях N = a²/λL. Фокс и Ли вычислили сдвиг фазы при однократном прохождении относительно геометрического сдвига фазы, т. е. 2πL/λ. Их результаты изображены на фиг. 12. Условие резонанса для n-й моды любого типа записывается следующим образом:

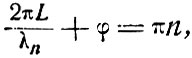
(7.12)

где λ_n = c/v_n, а φ - сдвиг фазы, соответствующий поперечной конфигурации. Из (7.12) следует

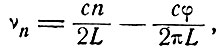
(7.13)

следовательно, разность частот соседних мод одного типа равна

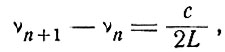
(7.14)

как и в случае плоской волны [см. (7.3)]. Однако частоты мод ТЕМ_00n и ТЕМ_10n, которые принадлежат различным поперечным конфигурациям, а именно ТЕМ₀₀ и ТЕМ₁₀, будут сдвинуты друг относительно друга, и этот сдвиг вычисляется на основе данных по сдвигу фаз, представленных, например, на фиг. 12.

Характер излучения лазера принципиально может быть определен из распределений фазы и амплитуды, которые для случая поперечных конфигураций получены Фоксом и Ли, хотя в их работе основной упор сделан не на более распространенных в лазерной технике интерферометрах, а на интерферометрах с низкими значениями N.

Плоско-параллельный интерферометр, образованный двумя параллельными плоскими зеркалами, не является наилучшим резонатором, имеющим много мод. Могут быть получены значительно лучшие результаты при использовании двух вогнутых сферических зеркал с конфокальной установкой их, т. е. установкой, когда центр сферы одного зеркала находится на поверхности другого зеркала. Такие сферические интерферометры были предложены Коном [19], который доказал, что эта система имеет большую разрешающую силу, чем система с плоскими зеркалами при таких же размерах. Схема интерферометра Кона изображена на фиг. 13.

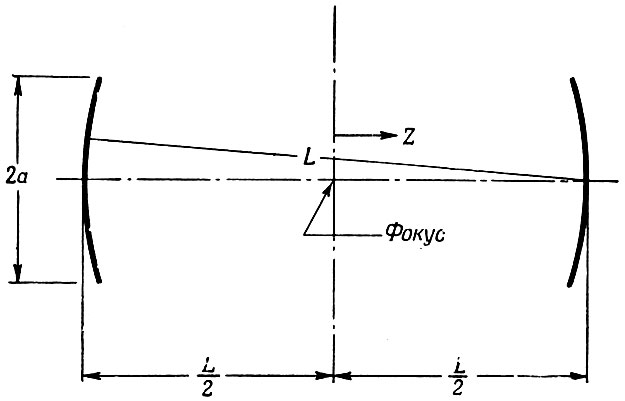
Фиг. 13. Интерферометр с конфокальными сферическими зеркалами

Фокс и Ли [24] вычислили несколько первых мод конфокального сферического интерферометра, используя при расчетах описанный ранее метод. В противоположность случаю плоских зеркал они получили следующие интересные особенности конфокальной системы. Поле значительно сильнее сконцентрировано около оси зеркала и падает до более низкой величины на краях по сравнению со случаем плоских зеркал. Амплитуды имеют плавное распределение. Неровности, изображенные на фиг. 10, отсутствуют. Поверхность зеркала является волновым фронтом волны. Потери в конфокальных системах на несколько порядков меньше, чем в сравниваемых системах с плоскими зеркалами. Фазовые сдвиги после одного прохождения для каждой конфигурации не зависят от N и являются кратными числами π/2 (см. фиг. 12).

Частотные соотношения (7.13) и (7.14) применимы и в случае конфокального интерферометра.

Численные расчеты работы Фокса и Ли были подтверждены и обобщены аналитическими расчетами Бойда и Гордона [12], которые решили интегральное уравнение, относящееся к конфокальному случаю.

Расчеты Бойда и Гордона показывают, что распределение амплитуды в центральной части зеркала описывается почти гауссовой кривой и что поверхность зеркала является поверхностью равной фазы в отличие от случая плоских зеркал. На поверхности зеркал амплитуда падает в 1/e раз от максимального значения в центре на расстоянии

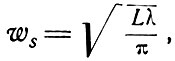
(7.15)

где L - радиус кривизны зеркал (см. фиг. 13). В действительности Бойд и Гордон получили выражения для амплитуды не только на поверхности зеркал, но также и в пространстве между ними. Они показали, что вблизи оси симметрии (ось z) поперечное распределение амплитуды падает по гауссову закону с шириной, меняющейся вдоль оси. Это изображено на фиг. 14. Приближенное изменение амплитуды имеет вид

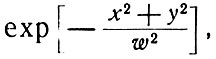
(7.16)

где

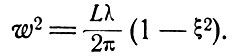
(7.17)

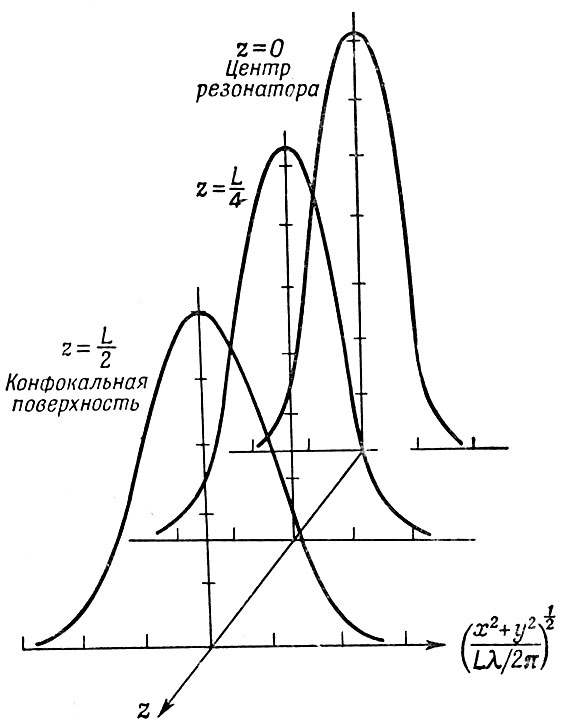
Фиг. 14. Распределение напряженности поля в случае конфокального резонатора для моды ТЕМ₀₀

Здесь ε = 2z/L - расстояние от фокуса, измеряемое в единицах фокальной длины. На поверхности зеркала ξ = 1 и w = w_s, в фокусе ξ = 0 и 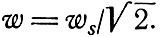Таким образом, сечение пучка в фокусе сжимается до половины его сечения на поверхности зеркал.

Чтобы получить угловую ширину пучка от излучающего пятна, возьмем отношение диаметра пятна, полученного из (7.17) при ξ→∞, к расстоянию от центра резонатора. Ширина пучка между точками, где мощность равна половине максимальной, определяется выражением

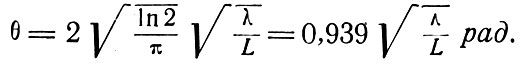
(7.18)

Численный множитель связан с шириной гауссовой кривой. Интересно отметить, что в эти формулы не входит радиус зеркала. Однако выражения (7.15), {7.17) и (7.18) применимы только в случае, когда a>3w_s. Следует также подчеркнуть, что аппроксимация в виде гауссовой кривой (7.16) несправедлива вблизи краев зеркала и что диаметр зеркала является важным параметром, когда рассматриваются дифракционные потери. Согласно Бойду и Гордону [12], дифракционные потери для однократного прохождения основной моды конфокального интерферометра составляют 10,9*10^-4,94N, где N = a²/λL, как и в случае интерферометра с плоскими зеркалами. Для простоты мы будем брать величину 11*10^-5N.

В таблице проводится сравнение между дифракционными потерями в случае интерферометров одинаковых размеров с плоскими и сферическими зеркалами.

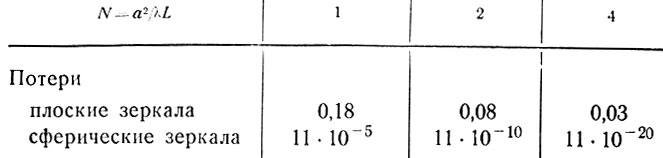
Все потери относятся к основным модам; величины для интерферометра с плоскими зеркалами взяты из кривых Фокса и Ли, приведенных на фиг. 10.

Очевидно, что дифракционные потери системы со сферическими зеркалами на несколько порядков меньше, чем для систем с плоскими зеркалами. Фокс и Ли обнаружили и ряд других важных преимуществ конфокальной сферической системы по сравнению с системой с плоскими зеркалами. Конфокальная система не является слишком критичной к взаимному согласованию зеркал. Конфокальные зеркала равной величины представляют особый случай двух вогнутых зеркал, повернутых друг к другу. Изменения размеров или кривизны зеркал так же, как и смещение вдоль оси одного из зеркал, отражаются довольно сложным образом на структуре мод. Эти свойства были детально проанализированы Бойдом и Когельником [98], которые пришли к выводу, что правильная конфокальная система является оптимальной по отношению к дифракционным потерям. Однако небольшое отклонение от одинаковой кривизны зеркал будет давать непропорциональное возрастание потерь в конфокальном случае; следовательно, чтобы обеспечить более стабильный режим, иногда желательно несколько нарушить правильную конфокальную геометрию или воспользоваться системой с плоским и сферическим зеркалами.

Можно отметить, что неполное отражение зеркал не меняет структуру моды в случае интерферометра с плоскими и сферическими зеркалами до тех пор, пока отражение однородно на всей поверхности зеркала [99].

Генерация когерентного излучения также наблюдалась с помощью резонаторов, взятых в виде небольших сфер [26].

Разные моды резонатора могут рассматриваться как почти независимые осцилляторы. Известно, что осциллятор характеризуется резонансной частотой и скоростью рассеяния энергии. Обычно скорость затухания описывается с помощью добротности Q, которая определяется формулой

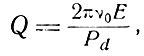
(7.19)

где v₀ - резонансная частота, E - энергия и P_d - скорость рассеяния энергии осциллятора. Если осциллятор возбуждается периодической силой с частотой v, то поглощаемая осциллятором мощность меняется в зависимости от v подобно описанной в § 6 функции g(v, v₀), причем полная ширина линии Δv заменяется выражением v₀/Q, которую мы будем считать шириной линии осциллятора или шириной моды резонатора. Большие значения Q соответствуют малым потерям и узкой линии.

В лазере имеет место сложное взаимодействие между совокупностью атомов и резонатором, допускающим многие резонансные частоты. Атомная система характеризуется центральной частотой v_a и шириной линии Δv, резонатор же характеризуется резонансными частотами с центральными частотами v₁, v₂, ..., v_n и соответствующими добротностями Q₁, Q₂, ..., Q_n. Прежде чем обсудить общую проблему взаимодействия, следовало бы рассмотреть взаимодействие атомной системы с резонатором, имеющим только одну моду в той же частотной области, что и частота атомной системы. Это обычно имеет место при рассмотрении работы мазеров.

В этом случае атомы и резонатор эквивалентны двум связанным резонансным контурам. Анализ этих систем с помощью классической теории показывает, что в случае, когда центральные частоты связанных контуров слегка отличны, частота их совместных колебаний в основном будет определяться контуром с большой добротностью Q. Пусть система 1 имеет резонансную частоту v₁ и ширину линии Δv₁. Колебания связанного контура будут происходить не на частоте v₁, а приблизительно на частоте

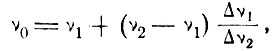
(7.20)

или, если выразить через добротность Q,

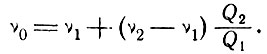
(7.21)

В случае мазера, работающего на пучке молекул аммиака, резонатор имеет одну резонансную частоту и низкую добротность Q, излучение же молекул характеризуется высоким значением Q. Следовательно, в этом случае частота системы очень близка к частоте излучения молекул. В случае лазеров резонатор обычно имеет много мод. В первом приближении можно пренебречь связью между ними. Все моды возбуждаются от одних и тех же атомных систем и теряют энергию частично за счет неполного отражения, частично за счет дифракции или выхода излучения через боковые стороны, если моды не являются аксиальными. Аксиальные моды имеют наименьшие потери, т. е. наибольшие значения Q.

Как только возбуждение достигает значения, при котором разность N₂ - N₁ достаточно велика, чтобы обеспечить вынужденное излучение, начинает возрастать энергия различных мод резонатора. Сила, действующая на эти моды, достигает наибольшего значения для частот, расположенных вблизи центра спектральной полосы излучения атомов v_a. С ростом интенсивности возбуждения преобладающая часть энергии распределяется между малым числом мод, которые имеют наибольшие значения Q и частоты которых находятся вблизи частоты, на которой интенсивность излучения атомов максимальна. Математическая теория такого процесса в случае резонатора, имеющего много мод, была развита Вагнером и Бирнбаумом [83], которые вычислили спектр излучаемых частот в зависимости от ширины линии излучения атомов и степени возбуждения. Опуская сложные математические выкладки Вагнера и Бирнбаума, мы можем качественно утверждать, что интенсивности мод, имеющих большую энергию, чем Другие моды, стремятся возрастать быстрее и скорость их возрастания увеличивается с увеличением Q. В то же время все моды черпают энергию из одной и той же совокупности возбужденных атомов; следовательно, более возбужденные методы возбуждаются еще больше, а интенсивность менее возбужденных мод уменьшается до тех пор, пока почти вся излучаемая энергия не сосредоточится в нескольких модах, имеющих "преимущества" по сравнению с другими. Двумя такими преимуществами, очевидно, являются: расположение вблизи центра v_a, что обеспечивает наибольшее возбуждение за счет излучения атомов, и высокое значение Q, которое позволяет интенсивности возбуждения данной моды возрастать быстрее по сравнению с другими.

Теперь очевидно значение соотношений, касающихся дифракционных потерь, введенных в начале этого параграфа. Величина Q для каждой моды определяется согласно формуле (7.19), в которой знаменатель P_d содержит сумму всех потерь данной моды. Потери, связанные с неполным отражением, остаются постоянными для всех мод; они определяются материалом отражающего слоя. Дифракционные же потери, как мы видим, различны для разных мод. Это различие скажется на зависимости Q от отношения дифракционных потерь к потерям при отражении. Если дифракционные потери для моды меньше половины потерь, имеющих место при отражении, то дальнейшее уменьшение дифракционных потерь не оказывает существенного влияния. Именно этот случай имеет место для основных мод конфокальных сферических резонаторов. Однако дифракционные потери резонаторов с плоскими зеркалами могут существенно влиять на величину Q в случае, когда размеры зеркал малы. Большие потери для неаксиальных мод обычно приводят к уменьшению Q до таких значений, при которых интенсивность возбуждения мод становится ничтожной и в работе такого лазера можно с большой точностью учитывать только аксиальные моды.

Энергетические потери для различных аксиальных (ТЕМ_00n) мод приблизительно равны. Как мы уже отметили, частоты этих мод расположены настолько близко друг к другу, что в пределы ширины спектральной линии атома попадают десятки и сотни различных мод. Обычно только некоторые из этих мод расположены настолько близко к максимуму спектральной линии излучения атома, что они возбуждаются одновременно. Однако даже небольшая разница в дифракционных потерях для различных мод может привести к невозможности возбуждения некоторых из них, так что если лазер работает при возбуждении, близком к выполнению условий самовозбуждения, то генерация будет осуществляться только с помощью мод, имеющих наименьшие потери.

В обсуждаемой в настоящем параграфе теории резонаторов, используемых в лазерах, предполагалось выполнение некоторых "идеальных" условий.

Наиболее важным из них было предположение о том, что активное вещество лазера однородно и изотропно. Используемые в лазерах кристаллы не являются изотропными, и если даже эти кристаллы практически однородны в невозбужденном состоянии, их возбуждение, как правило, неоднородно. Следовательно, предположение об изотропном веществе, обладающем однородным усилением и не имеющем внутреннего рассеяния, приводит к выводам, которые лишь частично применимы к объяснению экспериментов, выполняемых с использованием реальных несовершенных веществ.

Экспериментально наличие многих мод наиболее удобно наблюдать в лазерах, использующих газы. Наблюдение таких мод в лазере, использующем смесь газов He - Ne, обсуждается в § 17. Величину разделения этих мод по частоте можно получить смешением излучения этих мод и определением резонансной частоты. Такой метод трудно использовать для излучения рубина, так как излучение лазера, использующего кристалл рубина, не обладает необходимой стабильностью. Спектральное разделение аксиальных мод глубина может быть достигнуто только при использовании предельной величины разрешения спектрографов. Это было сделано Кифтаном, Кручковым и Кузианани [17], которые получили серию линий шириной 0,02 см^-1 разделенных друг от друга на 0,08 см^-1.

В 1962 г. появился ряд работ относительно неаксиальных мод в лазерах. Некоторые из них (например, работа Евтухова и Ниленда, см. § 9) связаны в основном с характером наблюдаемых освещенных пятен на торце кристалла рубина. Другие основываются на наблюдении характера излучаемого пучка. К этой категории относится работа Когельника и Ригрода [48], связанная с модами газового лазера со сферическими зеркалами.