Глава III. Некоторые вопросы теории

§ 6. Условия самовозбуждения

В § 3 мы указали на то, что описывающая поглощение кривая обычно имеет колоколообразную форму (см. фиг. 2). Не обсуждая физических процессов, определяющих форму этих кривых, мы отметим, что кривые, описывающие излучение и поглощение, могут быть с хорошей степенью точности представлены так называемой кривой Лоренца, изображенной на фиг. 7. Эта кривая описывается аналитическим выражением

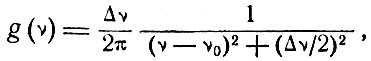
(6.1)

где v₀ - частота, соответствующая максимальному значению; Δv - частотная ширина между точками, в которых значение кривой g(v) равно половине максимального значения, как это изображено на фиг. 7. Множитель Δv/2π обусловлен следующей нормировкой площади, лежащей под всей кривой:

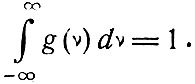
(6.2)

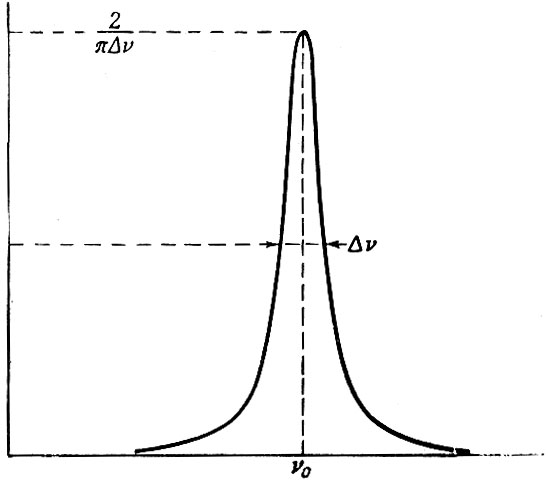
Фиг. 7. Кривая Лоренца

Тот факт, что интеграл в (6.2) простирается на отрицательную область частот, не является удивительным, так как практически площадь под кривой вне интервала частот v₀ - 2Δv до v₀ + 2Δv является незначительной, так что можно было бы в (6.2) проводить интегрирование в этом интервале частот. Когда будет необходимо указать частоту, соответствующую центру кривой Лоренца, мы будем писать g = g(v; v₀). Значение в максимуме кривой равно

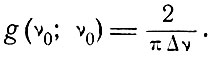
(6.3)

Введенный в § 3 коэффициент поглощения k_v может быть представлен в виде

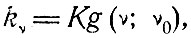
(6.4)

где K - интегральное поглощение для всей линии

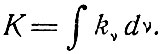
(6.5)

Эта величина была связана в § 3 с распределением атомов по энергетическим уровням и с временем жизни соответствующего перехода. Максимальное значение коэффициента поглощения следующее:

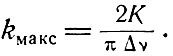
(6.6)

При заданной величине интегрального поглощения максимальное значение коэффициента поглощения обратно пропорционально ширине линии. Из эксперимента легче определить максимальное значение коэффициента поглощения узкой спектральной линии, чем интегральное поглощение. Если сравнить максимальный коэффициент поглощения k_макс для вещества, имеющего определенную населенность уровней, с максимальным значением коэффициента поглощения k₀ невозбужденного вещества (N₁ = N₀, N₂ = 0), то из (3.14) и (3.16) следует

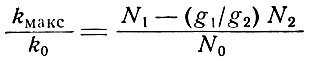
(6.7)

при условии, что форма линии поглощения остается неизменной.

Рассмотрим теперь совокупность атомов, в которой имеется инверсное распределение населенностей и которая обладает отрицательным поглощением в некоторой частотной области. Необходимым условием для этого является

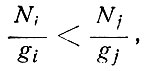
(6.8)

где E_i<E_j для некоторой пары уровней i и j. В таком веществе коэффициент k_v отрицателен вблизи частоты v₀ = (E_j - E_i)/h. Интенсивность параллельного пучка соответствующей частоты будет возрастать согласно уравнению

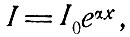
(6.9)

где α = -k_v При некоторых обстоятельствах это усиление света может привести к генерации света, т. е. осуществится лазерный режим работы.

Как мы уже видели, лазер представляет собой прибор, состоящий из двух параллельных зеркал, между которыми помещено вещество, имеющее отрицательное поглощение для некоторых частот. Схема этого прибора представлена на фиг. 8, где зеркала изображены отдельно от вещества, дающего усиление света (рубин). Однако такое отделение зеркал не является необходимым. Чтобы получить большую мощность на выходе из лазера, по крайней мере одно из зеркал делается частично прозрачным. Коэффициенты пропускания t, отражения r и потерь q связаны уравнением r + t + q = 1. В случае хороших многослойных диэлектрических зеркал коэффициент q исчезающе мал и мы можем написать t = 1 - r.

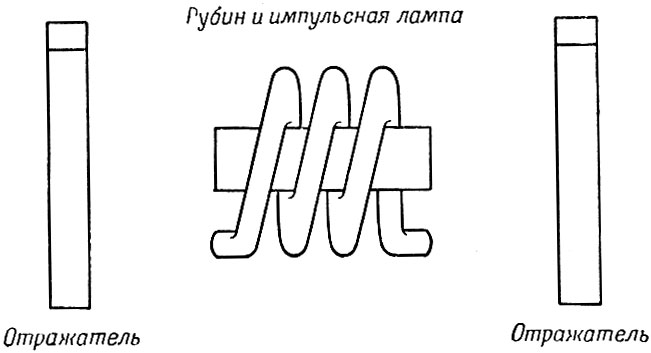
Фиг. 8. Схема лазера

В результате спонтанного и вынужденного излучения внутри активного вещества лазера происходит генерация света. Свет, который не выходит с боковых сторон, проходит всю длину активного вещества между зеркалами и отражается то от одного конца, то от другого. При каждом отражении теряется часть энергии, равная 1-r. Следовательно, генерация может существовать только в том случае, если увеличение интенсивности излучения, прошедшего всю длину кристалла, достаточно для того, чтобы компенсировать энергетические потери на конце и все потери, вызванные другими причинами. Излучение, вышедшее из точки, испытывает два отражения, прежде чем оно вернется в ту же самую точку, имея то же самое направление. При каждом таком прохождении через вещество интенсивность излучения увеличивается в e^αL раз. Если коэффициенты отражения на концах обозначить через r₁ и r₂, то увеличение интенсивности излучения характеризуется множителем F = r₁r₂e^2αL.

Введем средний энергетический коэффициент отражения r вместо r₁ и r₂, а также коэффициент потерь γ = -lnr^*. Прирост энергии в результате одного цикла (возвращения в ту же точку в том же направлении) есть

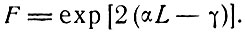
^* (В приводимой в конце книги табл. 5 указана область возможных значений r.)

Когда F≥1, генерация будет иметь место, начинаясь со спонтанных переходов; если F<1,, то первоначальный сигнал будет затухать. Очевидно, что в случае αL>γ интенсивность излучения на соответствующей частоте будет быстро возрастать до тех пор, пока она не станет настолько большой, что вынужденные переходы будут уменьшать населенность верхнего уровня и уменьшать значение α. Описание кинетики этого процесса встретится нам в связи с проблемой излучения гигантских импульсов в § 10. Чтобы рассмотреть подробно процесс генерации в стационарном или квазистационарном режиме, предположим, что имеется процесс стационарной генерации света соответствующей частоты, обусловленный спонтанным излучением и происходящий со скоростью, скажем, n квантов в сек. Пусть t обозначает коэффициент пропускания частично прозрачного зеркала. Тогда при каждом полном цикле прохождения между зеркалами в обоих направлениях теряется часть интенсивности, равная t, за счет выхода излучения наружу, а полная интенсивность увеличивается на множитель exp[2(αL - γ)]. Следовательно, мощность выходящего излучения будет равна

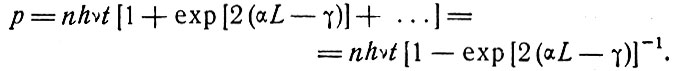
Мощность на выходе становится бесконечной, если значение αL будет равно или больше γ. Стационарная генерация может иметь место, однако, если максимальное значение α_макс коэффициента α(v) остается чуть меньше величины

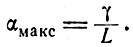
(6.10)

Равенство (6.10) называется условием самовозбуждения.

Так как величина α(v) почти равна α_макс в очень узкой спектральной области, то очевидно, что только в этой области усиление будет достаточным для возмещения потерь. Следовательно, лазер будет давать (резко суженное излучение, так что ширина его спектральной линии будет значительно уже, чем спектральная ширина линии излучения, испускаемого атомом. В § 8 мы увидим, как ширина спектра излучения лазера связана с шириной линии атомного спектра, с добротностью резонатора Q, образованного зеркалами лазера, а также с выходящей из лазера мощностью.

Вернемся к условию самовозбуждения. Величина α_макс может быть связана с N₁ и N₂ с помощью соотношений (3.14), (6.5) и (6.6). Комбинируя эти соотношения с (6.10), получаем

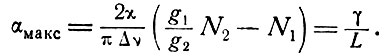
(6.11)

Следовательно,

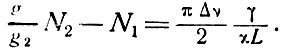
(6.12)

Это уравнение может быть использовано для определения минимальной величины N₂, если известна постоянная 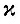. Если известен коэффициент k₀, можно воспользоваться уравнением (6.7) и написать условие самовозбуждения в следующем виде:

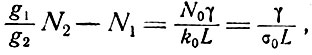
(6.13)

где отношение k₀/N₀ обозначено через σ₀ - максимальное поперечное сечение поглощения атома. Согласно измерениям Меймана и сотр. [59], величина σ₀ для линии рубина R₁ равна 2,5*10^-20 см².

Если отрицательное поглощение в веществе, создаваемое с помощью непрерывного возбуждения, имеет место в стационарном режиме, то левая часть соотношения (6.12) или (6.13) может быть связана со скоростью возбуждения. Мы покажем, как можно провести эти расчеты для кристалла рубина, в котором статистические веса сокращаются, так как g₁ = g₂^*. Следует осторожно подходить к учету множителя g₁/g₂ в формулах (6.12) или (6.13), чтобы избежать неоправданного исключения этого множителя в отдельных конкретных случаях. В ряде работ пренебрежение этим множителем там, где он был нужен, привело к ошибочным выводам.

^* (Строго говоря, для линии рубина R₁ не выполняется равенство g₁ = g₂. Практически, однако, сделанное предположение оправданно, так как имеется сильная связь между двумя двукратно вырожденными уровнями, дающими излучение, соответствующее линиям R₁ и R₂. Основной уровень в рубине четырехкратно вырожден.)

Населенность уровней трехуровневой системы с общим числом атомов N₀ определяется из следующих кинетических уравнений:

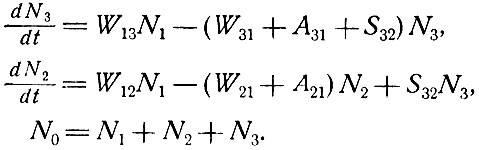
(6.14)

На фиг. 5 наглядно изображены описываемые этими уравнениями переходы с соответствующими обозначениями.

В уравнениях (6.14) W - вероятность вынужденного перехода, зависящая от плотности излучения, А - вероятность спонтанного перехода, S₃₂ - вероятность безызлучательного перехода с уровня 3 на уровень 2, N₀ - заданное полное число активных атомов в единице объема. В стационарном случае производные в (6.14) равны нулю, и мы можем найти решение для отношения N₂/N₁. В предположении, что вероятность спонтанного перехода с верхнего уровня A₃₁ мала по сравнению с вероятностями всех остальных переходов, получается простое решение. В этом случае

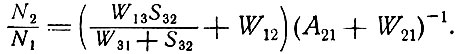
(6.15)

Возможно дальнейшее упрощение, если учесть, что вследствие соотношения Эйнштейна (3.4) W₁₃ = W₃₁ и W₂₁ = W₁₂, и если ограничиться только такими веществами, для которых вероятность безызлучательной релаксации между уровнями 3 и 2 велика, т. е. S₂₃>>W₁₃. При таком ограничении получаем

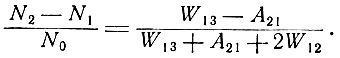
(6.16)

Величина W₁₃ пропорциональна интенсивности возбуждающего света, a W₁₂ пропорциональна интенсивности излучения лазера. (При подходе к условию самовозбуждения W₁₂ = 0.) Из (6.13) можно вычислить отношение (N₂ - N₁)/N₀, если заданы значения k₀, r и L. После этого, согласно выражению (6.16), может быть вычислено минимальное значение величины W_l3, необходимое для получения такого отношения.

Очевидно, что величина W₁₃ должна быть больше, чем A₂₁, так как для генерации недостаточно иметь равенство этих величин из-за неизбежных потерь при отражениях. Тем не менее условие W₁₃ = A₂₁ все же часто используется для оценки пороговой мощности, необходимой для начала генерации. В действительности же это только условие достижения отрицательного поглощения в веществе.

Для определения необходимой мощности возбуждения могут быть сделаны и еще более упрощенные вычисления. Предполагая, что возбуждение осуществляется с помощью плоской монохроматической волны с частотой v_p и что n есть число фотонов, падающих на единицу поверхности кристалла в единицу времени, получим следующие соотношения:

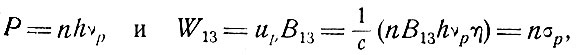
(6.17)

где величина

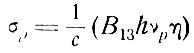
(6.18)

есть интегральное сечение поглощения для возбуждающего излучения [см. (3.12)]. Тогда для выполнения условия W₁₃≥A₂₁ плотность падающего потока излучения Р должна быть не менее чем

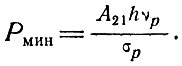
(6.19)

Облучение вещества с помощью плоской волны представляет собой лишь математическую абстракцию. Более реальным является изотропное облучение вещества почти через всю его поверхность. Более того, источник облучения подобен разряду в газе высокого давления с более или менее непрерывным спектром, сходным со спектром излучения абсолютно черного тела. Таким образом, вполне реально считать, что кристалл лазера подвержен изотропному излучению черного тела, и повторить предыдущие расчеты, учитывая конечную ширину и частотную зависимость сечения поглощения σ. Мейман и его сотрудники [58, 59] проделали эти расчеты и получили более точные формулы, чем (6.19), для оценки минимального возбуждающего потока, необходимого для получения отрицательного поглощения в рубине. Однако соотношение (6.19) содержит основные факторы, определяющие требуемую степень облучения вещества. Необходимая мощность возрастает пропорционально вероятности спонтанного перехода, следовательно, эта мощность обратно пропорциональна времени жизни в возбужденном состоянии.

Другой общий вывод может быть сделан с помощью соотношений (6:13) и (6.16). Так как интенсивность возбуждения определяет величину (N₂ - N₁)/N₀ и поскольку при инверсии эта величина должна превышать минимальную величину γ/k₀L, может быть найдено соотношение между коэффициентом отражения, определяющим величину γ, и длиной активного вещества лазера L. Любое уменьшение отражения должно быть компенсировано увеличением длины, в противном случае возрастет мощность, необходимая для выполнения условия самовозбуждения. Важным обстоятельством является также то, что генерация может быть сорвана уменьшением r, т. е. увеличением γ.

Мощность, генерируемая на частоте v₂₁ активным веществом однородно возбужденного лазера объемом V, есть

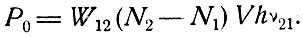
(6.20)

Здесь величина W₁₂ пропорциональна плотности излучения, а N₂ - N₁ зависит как от плотности излучения, так и от интенсивности возбуждения. При выполнении условия самовозбуждения появляется генерация излучения, по мере увеличения которой разность N₂ - N₁ уменьшается до тех пор, пока либо не наступит стационарный режим, либо плотность излучения не начнет опять падать и будет иметь место изменение интенсивности генерируемого света. Такое изменение интенсивности называется пульсацией.

Приближенное вычисление Р₀ для стационарного случая не представляет труда при условии W₂₁>>A₂₁, т. е. при условии, что сравнительно небольшое количество атомов испытает спонтанный переход с уровня 2. При этом на каждый поглощенный квант частоты v₃₁ = v_p испускается квант частоты v₂₁. В этом случае мощность вынужденного излучения, выходящего из лазера, в v₂₁/v_p раз меньше мощности, поглощаемой от возбуждающего источника. В течение квазистационарного режима работы число атомов, находящихся в основном состоянии, приближенно равно N₀V/2; таким образом, грубая оценка для выходящей мощности дает значение

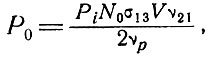
(6.21)

где P_i - полная интенсивность падающего света.

Стич [80] показал, что точное определение необходимой для возбуждения энергии требует более тщательных расчетов. Он вычислил, что для возбуждения пластинки из рубина необходима плотность потока около 600 ^вт/_см² при следующих условиях:

1. кристалл является оптически тонким,
2. возбуждение происходит с двух сторон и
3. вся возбуждающая энергия сосредоточена в полосе поглощения рубина.

Это значение очень хорошо согласуется с величиной 555 ^вт/_см², вычисленной другим способом Мейманом [59] для цилиндрического образца рубина.