§ 16. Условия возникновения инверсной населенности при возбуждении посредством электронных ударов

В § 15 мы отметили, что возникновение инверсной населенности в газовом разряде может быть достигнуто посредством электронных ударов. В газовом разряде имеют место различные процессы, и только в сравнительно редких случаях удается получить в стационарном режиме инверсную населенность по отношению к какой-либо паре энергетических уровней. В настоящем параграфе мы исследуем условия возникновения инверсной населенности.

В газовом разряде наиболее важными являются следующие процессы, приводящие к обмену энергией между частицами:

1. Электронные удары первого рода, при которых атом получает энергию от электрона.
2. Электронные удары второго рода, при которых атом передает свою энергию возбуждения электрону.
3. Спонтанное излучение возбужденных атомов.
4. Поглощение излучения атомами.
5. Вынужденное излучение атомов.

Скорость, с которой происходят эти процессы, определяется числом атомов в данном состоянии и вероятностями переходов в единицу времени для отдельного атома. Вероятность перехода в единицу времени относится к определенному состоянию атома и равна обратной величине времени жизни атома в данном состоянии.

Пусть 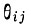означает время жизни для перехода атома с уровня i на уровень j при соударении с электронами с данной плотностью, находящимися в равновесии между собой при температуре T^*. Если бы не было каких-либо других процессов, кроме столкновений, то скорость изменения числа атомов на уровне i определялась бы формулой

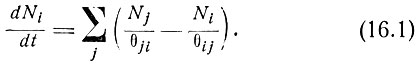
^* (Символ 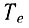более предпочтителен для обозначения электронной температуры, но мы здесь опускаем индекс e для упрощения написания формул.)

Покажем, что величины 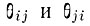связаны простым соотношением. При термодинамическом равновесии с температурой Т число атомов на каждом уровне постоянно. Тогда для любого i справедливо равенство

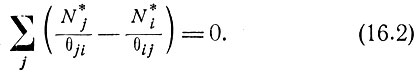
Более того, принцип детального равновесия требует, чтобы равенство (16.2) было справедливо для каждой пары уровней. Это означает, что для любых i и j должно иметь место соотношение

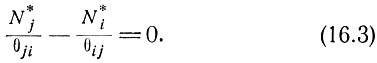
Следовательно,

Поскольку 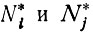представляют собой населенности уровней i и j при термодинамическом равновесии, то из (3.8) следует

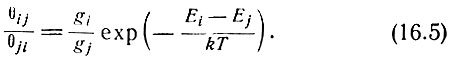
В случае, когда переходы атомов происходят не только в результате электронных ударов, но и под влиянием других причин, распределение не будет соответствовать формуле

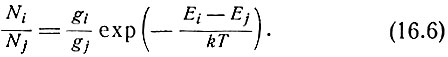
Это обстоятельство, однако, не влияет на справедливость формулы (16.5), представляющей собой соотношение между вероятностями переходов. Стационарное распределение может быть получено, если учесть все возможные процессы в уравнении для изменения числа частиц на данном уровне. В самом простом случае двух уровней, между которыми возможен спонтанный излучательный переход с временем перехода с уровня 2 на уровень 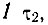, это уравнение имеет вид

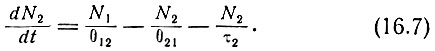
В стационарном состоянии

Если процесс излучения происходит сравнительно быстро, т. е. 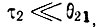то получим

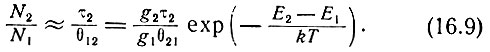
Отношение 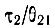представляет собой величину отклонения распределения от больцмановского. В значительной степени этот фактор находится под контролем экспериментатора, поскольку хотя τ₂ и фиксировано, но величина 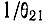пропорциональна плотности электронов в разряде. Однако отношение 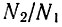не может расти беспредельно с увеличением плотности, поскольку применимость формулы (16.9) ограничена предположением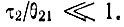

Введем теперь дополнительный уровень 3, расположенный выше уровня 2. Рассмотрим переходы между этими уровнями. При тех же предположениях получим

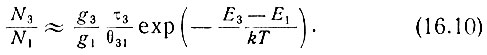
Из (16.9) и (16.10) можно получить

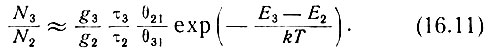
Несмотря на то, что экспоненциальный множитель всегда меньше единицы, величина, стоящая перед экспонентой, при определенных значениях параметров может значительно превышать единицу, в результате чего N₃ будет превышать ^* Это условие инверсной населенности или отрицательного поглощения. Для выполнения этого условия мы должны выбрать соответствующее вещество и соответствующие уровни энергии так, чтобы отношение 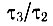было велико по сравнению с 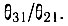В качестве одного из возможных примеров Джаван указал, что для уровней 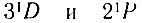гелия отношение 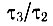составляет 35, а 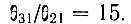В подобном случае возможно возникновение инверсной населенности. В действительности же существует множество пока еще неучтенных факторов, усложняющих ситуацию. Одним из них является наличие других энергетических уровней, также населенных в результате возбуждения электронными ударами. Если излучательные переходы с этих уровней происходят в основном на уровень 2, а не на уровень 3, то они будут препятствовать выполнению условия инверсной населенности, которое обычно выполняется с небольшим запасом.

^* (В оригинале опущено отношение статистических весов 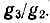- Прим. перев.)

Для выполнения условий самовозбуждения необходимо, чтобы не только величина N₃ превышала N₂, но и чтобы разность 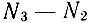была больше некоторого минимального значения. Следовательно, при прочих равных условиях желательно иметь разряд в газе с высокой плотностью. При высоких плотностях становится существенным процесс поглощения фотонов, спонтанно излучаемых возбужденными атомами. Процесс поглощения фотонов увеличивает время жизни атома в возбужденном состоянии. Этот процесс полезен только в том случае, когда он увеличивает время жизни атома на верхнем уровне 3, что будет иметь место, когда правилами отбора разрешены оптические переходы между уровнями 1 и 3. В этом случае система может работать при сравнительно высоких плотностях. Однако в случае, когда основной уровень связан с уровнем 2 разрешенным переходом, увеличение плотности нежелательно, так как оно приводит к увеличению населенности уровня 2. Эта неблагоприятная ситуация имеет место для уровней гелия 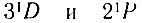, о которых говорилось выше.

Согласно теории квантовых переходов, в случае переходов, разрешенных правилами отбора, отношение 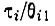остается постоянным для всех уровней. Как следует из (16.11), в этом случае невозможно получить отрицательное поглощение. Следовательно, по крайней мере один из двух уровней в системе должен соответствовать оптически запрещенному переходу в основное состояние. Этот уровень может быть возбужден электронными ударами, хотя эффективное поперечное сечение этого перехода, вообще говоря, меньше, чем для оптически разрешенного перехода, в благоприятном случае переход с нижнего уровня рабочего перехода должен быть запрещен, и слабое возбуждение этого уровня облегчает осуществление состояния с отрицательной температурой. Такая ситуация имеет место для неона, но пока состояние с инверсной населенностью в чистом неоне не получено^*. Причина этого, по-видимому, заключается в том, что нижний уровень рабочего перехода имеет избыточную населенность вследствие переходов с более высоких энергетических уровней неона.

^* (В работах [105-107] была получена генерация в чистом неоне.- Прим. перев.)

Первый и пока что единственный успешный метод получения состояний с отрицательной температурой в газах основан на взаимодействии атомов двух различных газов. Кинетика этого процесса была рассмотрена Басовым и Крохиным [5, 6], работа которых здесь кратко воспроизводится.

Обозначим два различных газа символами a и b. Атомы рабочего газа a имеют три уровня энергии: 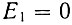- основной уровень, E₂ и E₃. Атомы вспомогательного газа b имеют два уровня 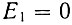и E₃. Совпадение или почти совпадение уровня 3 газов a и b является существенным обстоятельством в этой схеме, так как только в этом случае происходит заметная передача возбуждения между двумя атомами различных газов. Этот процесс называется резонансной передачей энергии.

Скорость изменения числа атомов газа a, находящихся на уровне E₃, равна

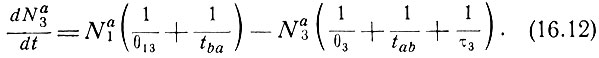
Здесь 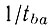- вероятность передачи энергии возбуждения при столкновении атома газа a, находящегося в основном состоянии, с возбужденным на уровень 3 атомом газа b; 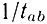- вероятность обратного процесса; 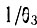- полная вероятность перехода с уровня 3 за счет электронных ударов второго рода, причем

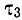
- время жизни по отношению к излучательному переходу уровня 3 на оба низлежащих уровня. Возбуждением с уровня 2 на уровень 3 здесь можно пренебречь, так как соответствующий член пропорционален 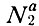и, следовательно, мал по сравнению с основными членами в (16.12).

Скорость изменения числа атомов 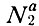на уровне E₂ определяется выражением

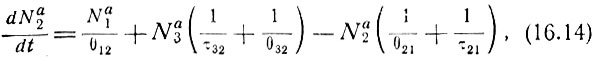
где τ - время жизни по отношению к излучательным переходам.

В стационарном случае производные по времени равны нулю. Условие возникновения отрицательного поглощения в переходах между уровнями E₃ и E₂ атомов газа a имеет вид

Если левую часть уравнений (16.12) и (16.14) положить равной нулю, то отношение 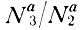можно выразить через времена жизни и вероятности переходов рассматриваемых уровней. Условие (16.15) дает тогда неравенство, зависящее от этих величин. Следует принять во внимание также соотношение (16.5) и то, что, согласно теории столкновений,

Это отношение определяет эффективную температуру возбуждения для атомов газа b, которую можно считать внешним параметром, поскольку мы интересуемся распределением атомов газа a. Условие (16.15) тогда дает

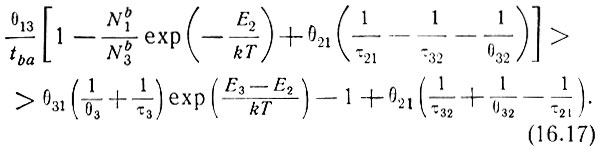
Отношения 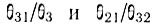не зависят от плотности электронов в разряде, а определяются поперечными сечениями соответствующих процессов и температурой электронов.

Неравенство (16.17) имеет разный смысл в различных областях изменения переменных 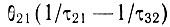и 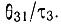Область значений этих переменных разделена на четыре части двумя кривыми. Уравнения этих кривых получаются приравниванием в формуле (16.17) выражения, заключенного в квадратные скобки, и выражения в правой части к нулю. В первом приближении можно пренебречь, величиной 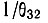по сравнению с 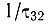и положить 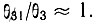В этом случае уравнения кривых переходят/в уравнения, описывающие прямые линии:

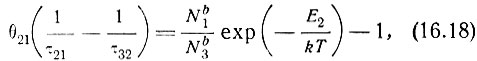
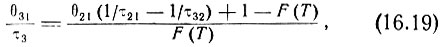
где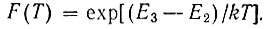

Ясно, что справа от вертикальной линии на фиг. 33, описываемой уравнением (16.18), когда правая часть отрицательна, условие (16.17) удовлетворяется при любых Эта ситуация соответствует области I на фиг. 33. В этом случае даже при возникает инверсная населенность и газ b не необходим. В области II инверсная населенность возникает в результате присутствия газа b. В области III газ b мешает образованию инверсной населенности, в области IV получение состояния с инверсной населенностью невозможно.

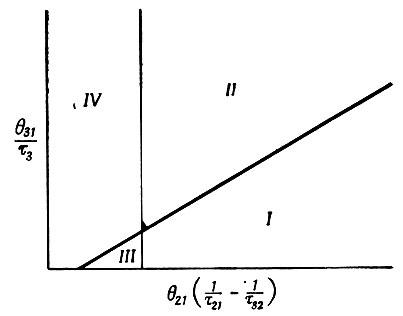
Фиг. 33. Диаграмма Басова-Крохина