Дополнение. О. Крохин, Ю. Попов. Полупроводниковые лазеры

1. Условия инверсной населенности в полупроводниках

Применение полупроводников в качестве рабочих материалов для лазеров привлекло к себе внимание в первую очередь возможностью осуществления непосредственного преобразования энергии электрического тока в энергию когерентного излучения. Полупроводники обладают рядом характерных свойств, среди которых от люминесцентных кристаллов их отличает электропроводность, а от газовых систем - весьма широкие линии излучения и возможность создания высокой концентрации активных частиц. Эти свойства полупроводников дают полупроводниковым лазерам ряд особенностей, главной из которых является высокий к. п. д. полупроводникового лазера, который может быть близок к 100%. Энергетический спектр полупроводника, обусловленный электронными состояниями, схематически изображен на фиг. I. В идеальном кристалле он представляет собой широкие полосы разрешенных состояний электронов: зону проводимости 1 и валентную зону 5, разделенные зоной запрещенных энергий 6. Энергетические состояния электронов в зоне проводимости и валентной зоне образуют практически непрерывный спектр собственных значений энергии Е(р), зависящей от импульса электрона^*. В неидеальном кристалле возникают уровни энергии 2, 3, 4, связанные с наличием тех или иных нарушений кристаллической структуры (примеси, вакансии, дислокации и т. д.). Как правило, эти состояния локализуются вблизи соответствующего центра в отличие от состояний в разрешенных зонах, принадлежащих всему кристаллу в целом.

^* (В случае периодических структур, каковыми являются кристаллы, более правильно говорить не об импульсе, а о квазиимпульсе, величина которого ограничена предельными значениями порядка ±πћ/a, где a - постоянная решетки.)

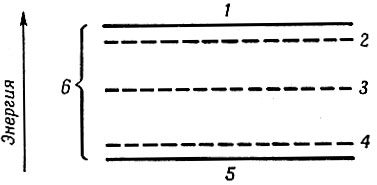
Фиг. I. Энергетические уровни полупроводника. 1 - зона проводимости; 2 - уровни доноров; 3 - глубокие уровни; 4 - уровни акцепторов; 5 - валентная зона; 6 - запрещенная зона

В идеальном полупроводнике при температуре абсолютного нуля валентная зона полностью занята электронами, а зона проводимости полностью свободна. В этом случае полупроводник не может проводить электрический ток и является изолятором. При температурах выше 0°К вследствие теплового возбуждения часть валентных электронов переходит в зону проводимости, в результате чего электрический ток может течь как за счет электронов в зоне проводимости, так и за счет свободных мест, образовавшихся в валентной зоне. В последнем случае обычно в рассмотрение вводят понятие "дырка", что соответствует незанятому электроном состоянию в валентной зоне. Дырка полностью эквивалентна частице с положительным зарядом и массой. Следует заметить, что электроны и дырки в кристалле имеют массу, отличную от массы свободного электрона и называемую эффективной массой. В идеальном полупроводнике число электронов в зоне проводимости в точности равно числу дырок в валентной зоне. Однако в реальном кристалле число носителей тока определяется в основном наличием примесей, которые можно разбить условно на следующие три группы:

1. примеси, уровни энергии которых, как правило, расположены близко к зоне проводимости 2, эти примеси легко отдают электроны в зону проводимости (доноры);
2. примеси, уровни энергии которых обычно расположены близко к валентной зоне 4, эти примеси легко захватывают электроны из валентной зоны, оставляя там дырки (акцепторы);
3. примеси, уровни энергии которых лежат глубоко в запрещенной зоне 3.

Для получения состояний с инверсной населенностью в полупроводниках могут быть использованы различные переходы электронов: зона - зона, зона - примесь и переходы между уровнями примеси.

При межзонных переходах следует различать два основных случая, определяемых структурой зон полупроводника: прямой переход, т. е. переход без изменения импульса электрона, и непрямой переход, при котором изменение импульса электрона компенсируется импульсом испускаемого или поглощаемого фонона.

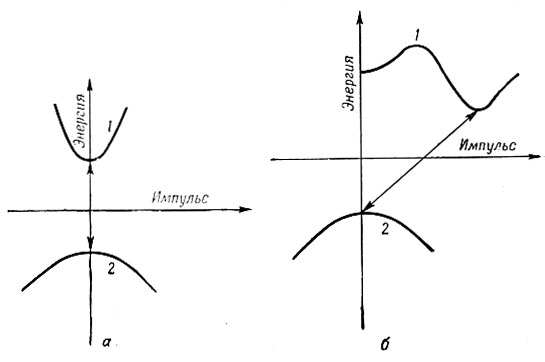
Фиг. II. Зависимость энергии носителей тока от импульса в полупроводниках. а - экстремальные значения энергии соответствуют одному значению импульса; б - экстремальные значения энергии соответствуют разным значениям импульса. 1 - зона проводимости; 2 - валентная зона

На фиг. II схематически изображена зависимость энергии электрона от импульса для зоны проводимости 1 и валентной зоны 2. Согласно закону сохранения импульса, при испускании или поглощении фотона должно выполняться равенство

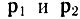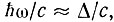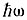где - начальный и конечный импульсы электрона, k - импульс фотона. Величина импульса фотона равна где - энергия кванта, c - скорость света, Δ - ширина запрещенной зоны. Отсюда следует, что для полупроводников, для которых 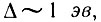величина k очень мала, т. е. меньше предельного импульса 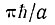на величину 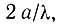где λ - длина волны излучения. Таким образом, переход с испусканием или поглощением фотона на диаграмме состояний фиг. II,a изображается вертикальной стрелкой и называется прямым переходом. Из фиг. II, а видно, что поглощению кванта минимальной энергии соответствует переход из максимума валентной зоны в минимум зоны проводимости. В этом случае прямой переход возможен только тогда, когда эти экстремальные значения энергии соответствуют одному и тому же значению импульса. То же относится и к процессу испускания фотона. В том случае, когда экстремальные значения энергии в зоне проводимости и валентной зоне соответствуют разным значениям импульса электрона (фиг. II, б), для выполнения закона сохранения импульса при переходе электрона необходимо испускание (или поглощение) фонона - кванта колебаний решетки кристалла, который практически полностью компенсирует разность импульсов конечного и начального состояний. При этом энергия фонона оказывается меньше энергии фотона. Это, конечно, справедливо, если переход осуществляется между экстремальными точками. Такой переход называется непрямым переходом, и закон сохранения импульса в этом случае имеет вид

где q - импульс фонона. Для получения состояния с инверсной населенностью в полупроводниках необходимо создание неравновесной концентрации электронов и дырок. Обычно электроны и дырки вследствие сильного взаимодействия с колебаниями решетки даже при неравновесных концентрациях характеризуются фермиевской функцией распределения по энергиям Е с температурой решетки Т:

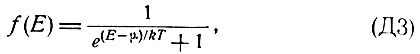
где μ - уровень Ферми (если концентрация 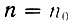равновесная) или квазиуровень Ферми (если концентрация n неравновесная), определяемый из условия нормировки

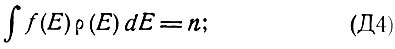
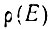
- плотность состояний в единичном интервале энергии,

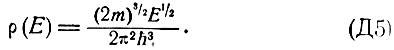
Для определения условия инверсной населенности необходимо потребовать, чтобы суммарное поглощение в данном переходе было отрицательным. Опуская спонтанное излучение, для прямых переходов имеем

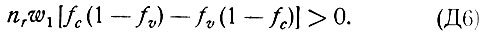
Здесь в силу принципа детального равновесия вероятность прямого и обратного процессов принята одинаковой и равной 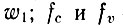- функции распределения электронов в зоне проводимости и валентной зоне; - число фотонов в заданном состоянии. Из (Д6) следует, что 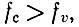т. е.

Условие (Д7) является основным условием инверсной населенности при прямых межзонных переходах в полупроводниках и показывает, что в этом случае электроны или (и) дырки должны быть вырождены.

В случаях непрямых переходов представляет интерес процесс одновременного испускания фотона и фонона. При этом процессе излучается наиболее длинноволновый фотон, энергия ћω которого равна начальной энергии электронно-дырочной пары (порядка 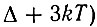минус энергия фонона 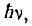, определяемая заданным значением импульса 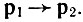При очень низких температурах число фононов в кристалле будет мало и обратный процесс, приводящий к поглощению фотона, будет подавлен, в то время как прямой процесс будет идти за счет спонтанного испускания фононов. В этом случае условие инверсии получается из неравенства

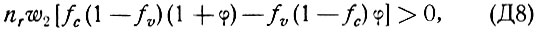
где 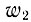- вероятность перехода, φ - число фононов в заданном состоянии,

Из (Д8) получаем

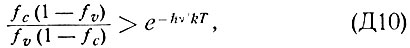
что эквивалентно неравенству

Условие (Д11) является условием инверсной населенности в случае непрямых межзонных переходов. Из (Д11) видно, что в случае, если , вырождения носителей тока не требуется; в противоположном случае непрямые переходы не дают преимущества по сравнению с прямыми. При условие инверсной населенности можно переписать в виде

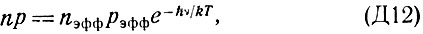
где n и p - концентрации электронов и дырок

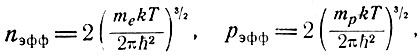
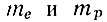
- эффективные массы электрона и дырки.

Интересна возможность непрямого перехода из экситонных состояний. В экситонном состоянии электрон и дырка связаны между собой подобно водородному атому с энергией связи

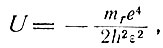
где 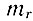- приведенная масса, ε - диэлектрическая проницаемость. Это обстоятельство приводит к увеличению вероятности перехода. Концентрацию η экситонов можно выразить через концентрацию свободных (невырожденных) электронов и дырок, предполагая, что между ними имеется термодинамическое равновесие,

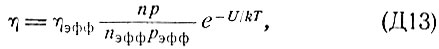
где 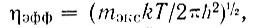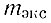- масса экситона. Условие инверсной населенности при переходе из экситонных состояний имеет вид

где 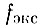- функция распределения экситонов, что с учетом (Д13) эквивалентно

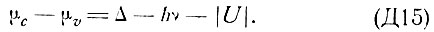
Как уже было замечено ранее, состояние с инверсной населенностью возможно получить также в переходах зона - примесь и между уровнями примеси. В первом случае следует, вообще говоря, различать два варианта: переход носителей из одной зоны на уровни примеси, расположенные вблизи края другой зоны, и переход на уровни, расположенные вблизи той же зоны.

В первом варианте вследствие быстрой релаксации носителей между примесью и близко расположенной к уровню примеси зоной заполнение уровня примеси будет определяться квазиуровнем Ферми носителей тока в этой зоне, и условие инверсной населенности примет вид

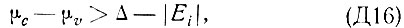
где 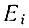- энергия связи носителя на примеси.

Во втором варианте, как и в случае переходов между уровнями примеси, условие инверсной населенности записывается, как в случае обычной двухуровневой квантовой системы (см. § 6).

Для усиления электромагнитной волны полупроводником необходимо, чтобы индуцированное усиление в переходе с инверсной населенностью превышало поглощение в результате всевозможных других процессов (поглощение примесями, свободными носителями и др.). В режиме генерации необходимо также выполнение условия самовозбуждения, которое зависит от потерь энергии излучения в объемном резонаторе. Для решения этих задач необходимо вычислить коэффициент усиления в переходе с инверсной населенностью. Для прямых межзонных переходов коэффициент усиления можно получить, записав в (Д6) явное выражение для вероятности перехода [1] и просуммировав по начальному и конечному состояниям с учетом законов сохранения.

В этом случае коэффициент усиления α₁ равен [2]

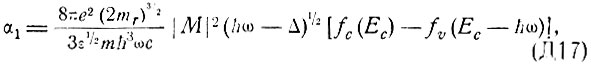
где 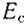- энергия электрона в зоне проводимости, M - матричный элемент. При непрямых переходах коэффициент усиления может быть получен из (Д8) суммированием по уровням валентной зоны и зоны проводимости с учетом закона сохранения энергии

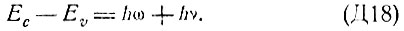
Выбирая за начало отсчета энергии край зоны проводимости, коэффициент усиления при непрямых переходах α₂ можно записать в виде

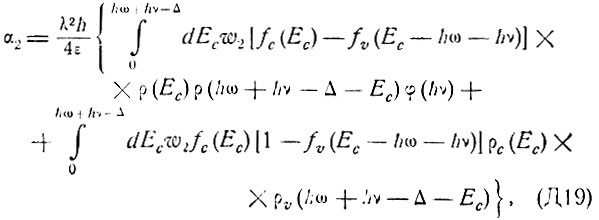
где плотность СОСТОЯНИЙ В зоне проводимости 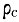и в валентной зоне 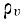дается формулой (Д5). Первое слагаемое в (Д19) соответствует поглощению, второе - усилению. В том случае, когда носители тока не вырождены, можно положить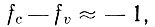 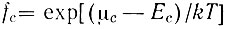и 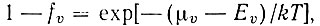тогда вычисление интегралов в (Д19) дает

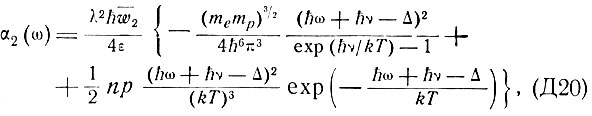
где представлено явное выражение для φ.

Из (Д20) видно, что при 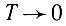первый член, соответствующий поглощению, становится малым.

Поглощение излучения в полупроводнике, как уже было отмечено ранее, может происходить на примесях, дефектах и свободных носителях тока. Поглощение решеткой становится существенным в дальней инфракрасной области спектра.

Коэффициент поглощения на примесях и дефектах k₁ может быть вычислен, если известно сечение поглощения фотона א, и выражается элементарной формулой

где N - плотность поглощающих центров. Поглощение на свободных носителях тока может происходить только в результате взаимодействия с решеткой, поскольку, как хорошо известно, свободная заряженная частица не может поглощать электромагнитную волну. Этот процесс может быть описан посредством диэлектрической проницаемости ε, мнимая часть корня квадратного из которой дает величину поглощения k₂:

где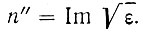

Согласно работе [1], диэлектрическая проницаемость ε равна

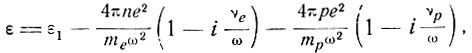
где 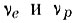- частоты соударений электронов и дырок в кристалле, определяющие проводимость полупроводника

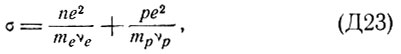
а 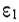- диэлектрическая постоянная без учета свободных носителей тока. В случае, когда имеет место соотношение

Если частоты соударений электронов и дырок с решеткой близки, т. е. 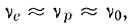то коэффициент поглощения можно записать в виде

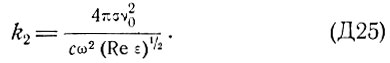
Иногда бывает удобно вводить сечения поглощения 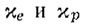фотона свободными носителями тока. Согласно (Д22)-(Д25),

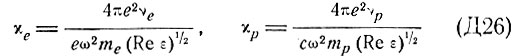
и

Как хорошо известно, прямые переходы в полупроводниках характеризуются сравнительно большой вероятностью перехода, превышающей вероятность поглощения на свободных носителях тока. Это обеспечивает возможность получения отрицательного коэффициента поглощения в прямых межзонных переходах. Однако в случае непрямых межзонных переходов оба процесса - поглощение на свободных носителях тока и непрямой переход - сопровождаются испусканием или поглощением фонона, что приводит к тому, что вероятности этих процессов могут иметь близкие значения. Это обстоятельство затрудняет получение отрицательного поглощения с использованием непрямых межзонных переходов. В этом случае необходим выбор такого полупроводника, который имеет большую вероятность непрямых переходов.

При непрямой рекомбинации экситона вероятность излучения w может быть вычислена из вероятности перехода свободных носителей тока В этом случае имеем [3]

где R - радиус экситона, равный по порядку величины 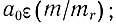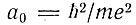- боровский радиус. Отношение интенсивности излучения, возникающего в результате непрямой рекомбинации экситонов, к интенсивности при непрямых переходах равно

с учетом (Д13) и (Д28) это отношение имеет вид

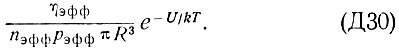
Вследствие того, что в выражение (ДЗО) входит малый множитель 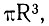это отношение может быть большим при низких температурах, что облегчает получение отрицательного поглощения при использовании переходов из экситонных состояний.