Глава 4. Контактные явления

§ 16. Работа выхода электронов из металла

Концентрация свободных электронов в металлах очень велика (порядка 10²³ см^-3). Находясь в постоянном хаотическом движении, они беспрерывно подходят к поверхности. Однако если металл не нагрет, то выхода электронов за пределы образца практически не наблюдается. Объясняется это следующим образом.

Внутри металла каждый свободный электрон при перемещении в межузельном пространстве взаимодействует со всеми окружающими его электронами, а также с положительно заряженными атомными остатками, создающими кристаллическую решетку. Благодаря равномерному распределению заряженных частиц в объеме кристалла равнодействующая всех сил, действующих на каждый электрон, оказывается в среднем практически равной нулю. При подходе же электрона к поверхности, а тем более при его выходе из кристалла равномерность распределения заряженных частиц вокруг него нарушается, и это приводит к возникновению сил, препятствующих выходу электрона за пределы кристалла. Можно рассмотреть две причины, затрудняющие выход электронов: образование у границы металла двойного электрического слоя и возникновение при выходе электрона так называемой силы зеркального отображения.

Двойной электрический слой. Даже при абсолютном нуле температуры свободные электроны в металле обладают достаточно большой кинетической энергией. Однако притяжение к узлам кристаллической решетки, заряженным положительно, не дает электрону покинуть металл совсем. Благодаря этому металл оказывается окруженным электронным облаком (рис. 43). Образующийся у поверхности двойной электрический слой можно рассматривать как плоский конденсатор, одной обкладкой которого являются приповерхностные положительные ионы, оставшиеся нескомпенсированными после ухода электронов, а другой - представленное в виде тонкого слоя электронное облако. Очевидно, что напряженность поля внутри такого конденсатора может считаться постоянной. Если а - расстояние между указанными обкладками, то сила F₁, препятствующая прохождению электрона, вычисляется по формуле

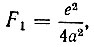
а энергия W₁, которую необходимо затратить электрону на преодоление двойного слоя, по формуле

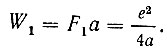
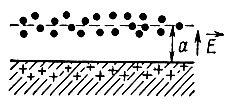
Рис. 43

Сила зеркального отображения. Преодолев двойной слой, электрон тем не менее еще не освобождается от воздействия со стороны металла. Дальнейшему удалению его препятствует сила зеркального отображения: на электрон, находящийся на расстоянии х от поверхности металла, действует со стороны этой поверхности сила, которая может быть определена как сила взаимодействия данного электрона с частицей, имеющей положительный заряд, равный модулю заряда электрона, и находящейся в глубине металлического тела на расстоянии х от поверхности (рис. 44). По закону Кулона сила зеркального отображения, действующая на электрон в вакууме, выражается формулой

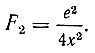
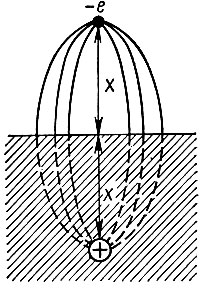
Рис. 44

Если предположить, что сила F₁ при выходе за пределы двойного слоя непрерывно переходит в силу F₂ то общий график силы, действующей на электрон по мере его удаления от поверхности металла, можно представить кривой, приведенной на рисунке 45. Энергия же, необходимая для преодоления силы зеркального отображения, равна

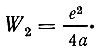
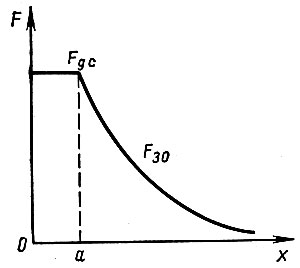
Рис. 45

Полная работа выхода. Электрон, покидающий металл, должен преодолеть своеобразный потенциальный барьер, показанный на рисунке 46. Часть этого барьера (на участке от 0 до а) создана силами двойного слоя, а другая часть (на участке от а до ∞) - силами зеркального отображения. Общая же высота W₀ потенциального барьера равна той работе, которую должен совершить электрон на пути от поверхности металла до полного отделения от металла. Величина W₀ называется полной работой выхода. Экспериментально определенные значения полной работы выхода для различных металлов лежат в интервале от 3 до 20 эВ.

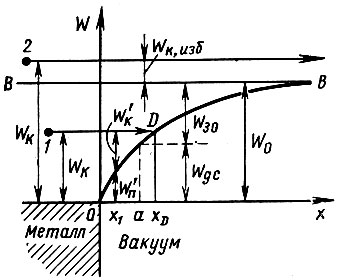
Рис. 46

Ход потенциального барьера можно рассматривать как кривую, отражающую изменение потенциальной энергии электрона по мере его удаления от поверхности металла. Действительно, электрон, находящийся внутри металла и обладающий некоторой кинетической энергией W_к (рассмотрим, например, электрон, обозначенный цифрой 1), может перемещаться в любом направлении без изменения энергии. Однако если он переходит границу металла - вакуум, то кинетическая энергия электрона в соответствии с законом сохранения энергии начинает превращаться в потенциальную. Так, если электрон отошел от границы на расстояние x₁, то часть его кинетической энергии перейдет в потенциальную W'_п. Поскольку, дойдя до точки хи электрон сохранил еще часть кинетической энергии он может и дальше уходить от поверхности. Однако при удалении электрона на расстояние x_D уже вся его кинетическая энергия преобразуется в потенциальную (точка D на кривой потенциальной энергии электрона). В этой точке скорость электрона оказывается равной нулю, после чего он возвращается обратно.

Для того чтобы электрон имел возможность окончательно покинуть металл, его кинетическая энергия должна быть не меньше высоты потенциального барьера W₀. Такой возможностью обладает, например, электрон, обозначенный на рисунке цифрой 2. Более того, поскольку начальная кинетическая энергия этого электрона превышает полную работу выхода, то, даже покинув металл, он сохранит некоторую скорость, соответствующую оставшейся неизрасходованной избыточной кинетической энергии:

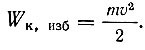
Обычно за нулевой уровень отсчета энергии принимают не уровень неподвижного электрона в глубине металла, а уровень, соответствующий неподвижному электрону, находящемуся в вакууме достаточно далеко от поверхности металла и не испытывающему воздействия с его стороны. На рисунке 46 это уровень ВВ, к которому асимптотически приближается кривая потенциальной энергии электрона. В этом случае объем металла является для электрона потенциальной ямой, глубина которой равна W₀. При таком выборе нулевого уровня электроны, находящиеся внутри металла и расположенные ниже уровня ВВ, имеют отрицательную энергию. О полной же работе выхода тогда говорят, что это работа, которая должна быть совершена электроном, первоначально находившимся на дне потенциальной ямы, при его выходе из этой ямы.