
§ 17. Уровень Ферми в металлах и функция распределения Ферми-Дирака
Уровень Ферми. Несмотря на огромное количество свободных электронов в металле, располагаются они по энергетическим уровням потенциальной ямы в строгом порядке. Каждый из электронов занимает вакантное место на возможно более низком уровне. И это вполне естественно, так как всякая система, будучи предоставлена самой себе, то есть в отсутствие внешнего воздействия, всегда стремится перейти в состояние с наименьшей энергией. Распределение электронов по уровням подчинено принципу Паули, согласно которому никакие две частицы не могут находиться в совершенно одинаковых состояниях. В силу этого на каждом энергетическом уровне может расположиться не более двух электронов, да и то имеющих различные направления спинов. По мере укомплектования нижних уровней происходит заселение все более высоко расположенных уровней. Если в рассматриваемом образце металла имеется N свободных электронов, то в отсутствие теплового возбуждения, то есть при абсолютном нуле температуры (T = 0), все свободные электроны разместятся попарно на N/2 нижних уровнях (рис. 47). Самый высокий энергетический уровень потенциальной ямы металла, занятый электронами при Т = 0, называется уровнем Ферми* и обозначается буквой μ или WF. Энергия электрона, находящегося на этом уровне, называется энергией Ферми. Все энергетические уровни, расположенные выше уровня Ферми, при Т = 0 оказываются абсолютно пустыми.
* (Свое название этот уровень получил в честь выдающегося итальянского физика Э. Ферми, разработавшего совместно с известным английским физиком П. Дираком теорию поведения коллективов частиц, ведущих себя как электроны в металле.)
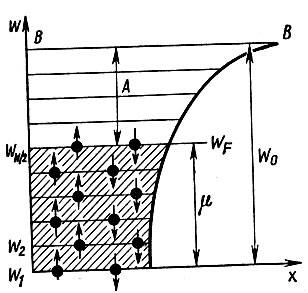
Рис. 47
Вполне очевидно, что для выхода электронов, находящихся на уровне Ферми, за пределы металла должна быть совершена работа
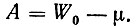
Величина А, равная энергетическому расстоянию между уровнем удаленного электрона ВВ и уровнем Ферми, называется термодинамической работой выхода или просто работой выхода. Именно эта величина определяет поведение различных металлов при установлении контакта между ними или при создании контакта металл - полупроводник.
Функция распределения Ферми - Дирака. Характер распределения частиц по разным уровням или состояниям в тех или иных условиях определяется так называемой функцией распределения. В общем случае функция распределения описывает вероятность занятости того или иного уровня частицами. Если достоверно известно, что данный уровень заселен частицей, то говорят, что вероятность обнаружения частицы на этом уровне равна 1. Если же с полной достоверностью можно сказать, что на рассматриваемом уровне нет частиц, то говорят, что вероятность обнаружения частиц в рассматриваемом состоянии равна 0. Однако во многих случаях нельзя достоверно утверждать, что уровень заполнен или пуст. Тогда вероятность нахождения частицы на рассматриваемом уровне отлична от нуля, но меньше единицы. При этом чем больше вероятность обнаружить частицу на рассматриваемом уровне, тем ближе к единице оказывается значение функции распределения для соответствующего состояния.
Если по оси абсцисс откладывать значения энергии, соответствующей разным уровням, от дна потенциальной ямы до ее потолка, а по оси ординат - вероятность заполнения электронами соответствующих уровней, то мы получим график функции распределения Ферми - Дирака 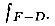 При Т = 0 он имеет вид, приведенный на рисунке 48. Часто этот график называют ступенькой Ферми. Из него видно, что при Т = 0 все уровни, вплоть до уровня Ферми, оказываются занятыми электронами. В точке W = μ функция распределения скачкообразно падает до нуля; это значит, что все уровни, расположенные выше уровня Ферми, пусты.
При Т = 0 он имеет вид, приведенный на рисунке 48. Часто этот график называют ступенькой Ферми. Из него видно, что при Т = 0 все уровни, вплоть до уровня Ферми, оказываются занятыми электронами. В точке W = μ функция распределения скачкообразно падает до нуля; это значит, что все уровни, расположенные выше уровня Ферми, пусты.
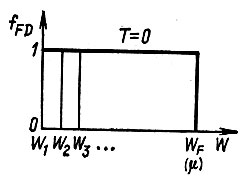
Рис. 48
Влияние температуры. При температурах, отличных от нуля, вид графика зависимости 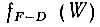 отличается от приведенного на рисунке 48. Повышение температуры приводит к появлению теплового возбуждения электронов, которое они получают от тепловых колебаний кристаллической решетки. Благодаря этому возбуждению часть электронов, расположенных на наиболее высоких заполненных уровнях, переходит на пустые уровни, лежащие выше уровня Ферми (рис. 49). Вероятность обнаружения электронов на этих уровня становится уже отличной от нуля. Одновременно с этим из-за ухода части электронов с некоторых уровней, расположенных непосредственно под уровнем Ферми, вероятность заполнения их окажется меньше единицы. Таким образом, повышение температуры приводит к некоторому "размытию" границы ступеньки Ферми: вместо скачкообразного изменения от 1 к 0 функция распределения совершает плавный переход. На рисунке 50 пунктиром показан вид графика функции распределения электронов по уровням при Т = 0, а сплошными линиями отражены распределения электронов при температурах, отличных от нуля. Площадь криволинейного треугольника, расположенного под кривой распределения правее значения WF (площадка 2), пропорциональна числу электронов, перешедших на возбужденные уровни, а площадь такого же треугольника, расположенного слева от значения WF над кривой распределения (площадка 1), пропорциональна числу электронов, ушедших с уровней, которые ранее были заполненными, то есть числу освободившихся под уровнем Ферми мест. Понятно, что площади этих двух треугольников одинаковы, так как с разных позиций они выражают одно и то же число электронов.
отличается от приведенного на рисунке 48. Повышение температуры приводит к появлению теплового возбуждения электронов, которое они получают от тепловых колебаний кристаллической решетки. Благодаря этому возбуждению часть электронов, расположенных на наиболее высоких заполненных уровнях, переходит на пустые уровни, лежащие выше уровня Ферми (рис. 49). Вероятность обнаружения электронов на этих уровня становится уже отличной от нуля. Одновременно с этим из-за ухода части электронов с некоторых уровней, расположенных непосредственно под уровнем Ферми, вероятность заполнения их окажется меньше единицы. Таким образом, повышение температуры приводит к некоторому "размытию" границы ступеньки Ферми: вместо скачкообразного изменения от 1 к 0 функция распределения совершает плавный переход. На рисунке 50 пунктиром показан вид графика функции распределения электронов по уровням при Т = 0, а сплошными линиями отражены распределения электронов при температурах, отличных от нуля. Площадь криволинейного треугольника, расположенного под кривой распределения правее значения WF (площадка 2), пропорциональна числу электронов, перешедших на возбужденные уровни, а площадь такого же треугольника, расположенного слева от значения WF над кривой распределения (площадка 1), пропорциональна числу электронов, ушедших с уровней, которые ранее были заполненными, то есть числу освободившихся под уровнем Ферми мест. Понятно, что площади этих двух треугольников одинаковы, так как с разных позиций они выражают одно и то же число электронов.
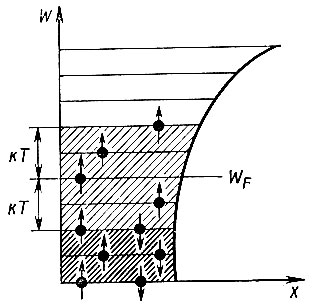
Рис. 49
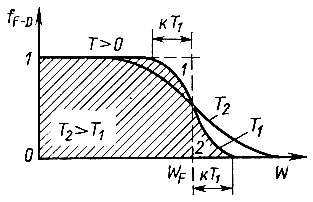
Рис. 50
Следует отметить, что в диапазоне рабочих температур степень размытия кривой распределения электронов в металле очень невелика. Объясняется это тем, что тепловому возбуждению подвергаются только те электроны, которые расположены на энергетических уровнях, непосредственно примыкающих к уровню Ферми. Можно качественно оценить энергетическую глубину залегания уровней, подвергающихся возбуждению. Из молекулярной физики известно, что кинетическая энергия частиц, обусловленная тепловым движением, выражается так:
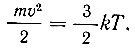
Следовательно, значение энергии, которую могут передать электронам испытывающие тепловые колебания атомы кристаллической решетки, по порядку величины равно kT. При комнатной температуре 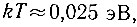 в то время как энергия Ферми для металлов при этой температуре лежит в диапазоне от 3 до 10 эВ. Поэтому оказывается, что в обычных условиях в переходах на более высокие энергетические уровни могут принимать участие не более 1% всех свободных электронов. Причем это как раз те электроны, энергия которых близка к энергии Ферми. Что же касается электронов, заселяющих энергетические уровни, расположенные в глубине потенциальной ямы и удаленные от уровня Ферми больше чем на kT, то они не принимают участия в тепловом возбуждении, из-за чего распределение этих электронов остается таким же, как и при абсолютном нуле.
в то время как энергия Ферми для металлов при этой температуре лежит в диапазоне от 3 до 10 эВ. Поэтому оказывается, что в обычных условиях в переходах на более высокие энергетические уровни могут принимать участие не более 1% всех свободных электронов. Причем это как раз те электроны, энергия которых близка к энергии Ферми. Что же касается электронов, заселяющих энергетические уровни, расположенные в глубине потенциальной ямы и удаленные от уровня Ферми больше чем на kT, то они не принимают участия в тепловом возбуждении, из-за чего распределение этих электронов остается таким же, как и при абсолютном нуле.
Физический смысл уровня Ферми. Обсуждая в §6 способность твердых тел проводить электрический ток, мы пришли к выводу, что проводимость связана с возможностью перехода электронов на более высокие энергетические уровни, то есть определяется возможностью получения электронами ускорения во внешнем электрическом поле. В металлах при Т > 0 такая возможность имеется только у электронов, находящихся в области размытия функции распределения, так как реальные электрические поля не в состоянии вырвать электроны из глубины потенциальной ямы и перевести их на свободные уровни, энергия которых выше WF (перейти же на соседние, более высоко расположенные уровни глубинные электроны не могут, потому что все эти уровни заняты). Следовательно, при Т > 0 энергия Ферми имеет смысл наиболее вероятной или средней энергии электронов металла, могущих принять участие в проводимости при данной температуре. Эти электроны ответственны не только за создание электрической проводимости. Именно они определяют вклад электронной теплоемкости в общую теплоемкость кристалла и в значительной степени определяют теплопроводность кристалла.
Уровень Ферми в металлах практически не изменяет своего положения по мере повышения температуры. С ростом температуры степень возбуждения электронов растет, и они переходят на более высоко расположенные уровни. Одновременно с этим возбуждению подвергаются и все более глубоко расположенные уровни, имеющие меньшую энергию. Кривая распределения при Т2 > Т1 (см. рис. 50) "размывается" более сильно, чем при T1, но в равной степени вправо и влево. Поэтому средняя энергия электронов, принимающих участие в проводимости, остается практически неизменной. Это тем более справедливо, что между возбужденными уровнями идет постоянный обмен электронами.
|
ПОИСК:
|