Ключ к системе ключей

((Длинное письмо в редакцию))

Ранее было высказано мнение, что система дверных ключей в нашем институте сложнее, чем теория поля. Это явное извращение фактов, и чтобы его опровергнуть, в настоящем сообщении мы излагаем упрощенную теоретическую схему, на основе которой создавалась эта система.

Начнем с определений.

Ключ состоит из стержня, на котором укреплены штифты.

Замок состоит из щели с отверстиями, расположенными соответственно позициям штифтов на стержне ключа. Кроме того, в замке имеется система рычажков, находящихся позади отверстий (см. рисунок).

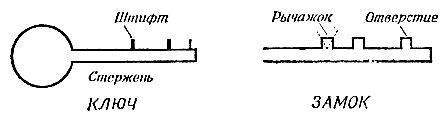
Рисунок

Введем теперь следующие три аксиомы:

1. Штифты поворачивают рычажки; для того чтобы замок открылся, все рычажки в замке должны быть повернуты.

2. Если в данной позиции нет штифта, отверстия или рыча лека, мы будем говорить в дальнейшем о наличии в данной позиции антиштифта, антиотверстия или антирычажка соответственно.

3. Ни в одном замке нет рычажков за антиотверстиями, ибо такой замок нельзя было бы открыть.

Пусть штифты, отверстия и рычажки описываются значением 1 переменных a_i, b_i и c_i соответственно. Индекс i - номер позиции. Антиштифты, антиотверстия и антирычажки соответствуют значению 0 тех же переменных. Определим теперь матричное умножение следующим способом:

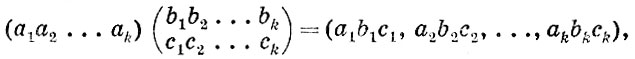
(1)

где символическое произведение abc=a, если одновременно a≤b и a≥c, в противном случае abc=1-a. Отсюда следует, что если (a₁ a₂...a_k) есть собственный вектор оператора

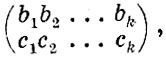
то ключ может отпереть замок.

Используя этот формализм, легко найти полное число ключей, которые открывают данный замок .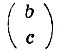

Оно равно

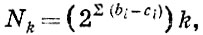
(2)

а число замков, которые могут быть открыты данным ключом (a), равно

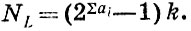
(3)

При получении этих выражений учитывался тот факт, что замок (0/0) есть тривиальный антизамок. В уравнениях (2) и (3) к есть сумма коэффициентов Клебша - Гордана, равная единице.

Развитый выше формализм позволил решить следующую задачу. Пусть некто хочет пройти из некоторой комнаты A через несколько дверей в произвольную комнату B. Число ключей, необходимое для этого, максимизировалось при произвольном выборе комнат A и B. (Проблема минимизации не решалась, поскольку ее решение тривиально - одинаковые замки.) Затем сотрудники института были разбиты на ряд подгрупп, и система ключей строилась таким образом, чтобы одновременно выполнялись два условия:

1) ни одна подгруппа не в состоянии открыть все те замки, которые могут быть открыты любой другой подгруппой;

2) трансформационные свойства групп соответствуют возможности одалживания ключей.

Создатели системы ключей надеялись, что она является единственно возможной и полной, и до известной степени это справедливо. Однако оказалось, что ключи, которые не должны были бы открывать некоторые двери, открывают их, если их вставлять в замок не до конца. Например, ключ (11111) может открыть замок 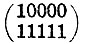в n=5 различных положениях. Число n было названо странностью системы ключ - замок. Экспериментальными исследованиями было найдено, что наша система ключей является весьма странной. Однако этот недостаток можно исправить, если потребовать для последней позиции соблюдения равенств a_k=b_k=c_k=1. Будем надеяться, что при ближайшем пересмотре системы ключей в нее будет внесено это исправление.

На отмычки настоящее исследование не распространяется.

Автор выражает благодарность сотрудникам, работающим в разных группах, за горячее обсуждение затронутых проблем.

Нильс Бор любил ходить в кино, причем из всех жанров признавал только один - ковбойские вестерны. Когда Бор по вечерам начинал жаловаться на усталость и рассеянность и говорил, что "надо что-то предпринять", все его ученики знали, что лучший способ развлечь профессора - сводить его на что-нибудь вроде "Одинокого всадника" или "Схватки в заброшенном ранчо". После одного из таких просмотров, когда по дороге домой все подсмеивались над непременной и избитой ситуацией - герой всегда хватается за револьвер последним, но успевает выстрелить первым, - Бор неожиданно стал утверждать, что так на самом деле и должно быть. Он развил теорию, согласно которой злодей, собирающийся напасть первым, должен сознательно выбрать момент, когда начать движение, и это замедляет его действия, тогда как реакция героя - акт чисто рефлекторный, и потому он действует быстрее. С Бором никто не соглашался, разгорелся спор. Чтобы разрешить его, послали в лавку за парой игрушечных ковбойских револьверов. В последовавшей серии "дуэлей" Бор, выступая в роли положительного героя, "перестрелял" всех своих молодых соперников!

Трудно себе представить, что привлекало Бора в этих картинах. "Я вполне могу допустить, - говорил он, - что хорошенькая героиня, спасаясь бегством, может оказаться на извилистой и опасной горной тропе. Менее вероятно, но все же возможно, что мост над пропастью рухнет как раз в тот момент, когда она на него ступит. Исключительно маловероятно, что в последний момент она схватится за былинку и повиснет над пропастью, но даже с такой возможностью я могу согласиться. Совсем уж трудно, но все-таки можно поверить в то, что красавец ковбой как раз в это время будет проезжать мимо и выручит несчастную. Но чтобы в этот момент тут же оказался оператор с камерой, готовый заснять все эти волнующие события на пленку, - уж этому, увольте, я не поверю!"