Температурные шкалы и идеальный газ

Итак, мы подошли к первому определению температуры. Температура - это некая характеристика тела, которая имеет одинаковое значение для всех тел, находящихся в тепловом равновесии. Но для количественных оценок теплового поведения тел мы должны ввести стандартный способ задания температуры. И здесь нам необходимо устройство, с помощью которого мы можем измерять какой-либо доступный для наблюдения параметр, изменение которого согласуется с изменением температуры. Такое устройство называется термометром. При измерении температуры тела термометр, соприкасаясь с ним, приходит с телом в состояние равновесия и показывает общую температуру системы в значениях измеряемого параметра, например высоты столбика ртути или электрического сопротивления проводника. Основная трудность при этом заключается в том, что различные измеряемые параметры по-разному зависят от температуры, поэтому показания подобных термометров необходимо приводить в соответствие со стандартной шкалой температуры.

Наибольшее распространение в качестве стандартной получила температурная шкала идеального газа. Считается, что внутренняя энергия идеального газа равна кинетической энергии его молекул. Зависимость температуры идеального газа от его внутренней энергии проста. Свойства идеального газа изучаются в рамках так называемой кинетической теории газов. Систематическое изложение этой теории в последнее время приписывается немецкому физику Рудольфу Клаузиусу (1857), хотя определенные ее положения возникли и получили распространение по крайней мере столетием раньше. Согласно этой теории, молекулы газа ведут себя подобно классическим частицам, то есть движутся независимо друг от друга и их отталкивание от стенок сосуда совершается без потерь энергии.

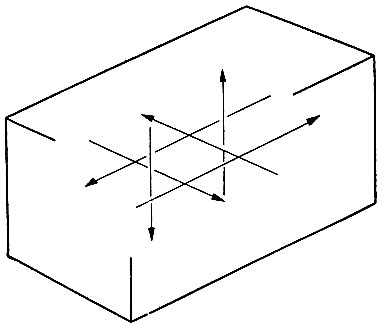
Рис. 16. Движения молекул согласно кинетической теории газов

Движение молекул в закрытом сосуде (рис. 16) в любой момент времени можно условно изобразить в виде двух равных и противоположно направленных потоков в каждом из трех взаимно перпендикулярных направлений. Предположим, что один из этих потоков движется параллельно стороне сосуда длиной L. Пусть масса каждой молекулы равна m, а средняя скорость - v. Если в сосуде N молекул, а в каждом потоке соответственно N/6, то за некий малый интервал времени t достигнет противоположной стенки и ударится о нее ^Nvt/_6l молекул. Давление в сосуде не изменяется, поскольку при соударениях молекул со стенкой потерь энергии не происходит. В этом случае лишь меняется направление скорости v. Произведение m*v называется количеством движения, или импульсом молекулы. При изменении направления скорости общее изменение количества движения молекулы составляет 2mv. За время t изменение количества движения всех молекул равно ^(Nvt*2mv)/_6l. Согласно второму закону Ньютона, сила, с которой молекула давит на стенку, равна скорости изменения общего количества движения молекул, или ^2Nmv2/_6l. Тогда давление p находится из соотношения

Произведение Al равно объему V сосуда, поэтому

Очевидно, что для других стенок сосуда эта величина определяется аналогично. Поскольку кинетическая энергия E молекулы равна ^mv2/₂, окончательно получаем:

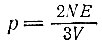
или

Давление p и объем V газообразного тела легко измерить. Еще в 1660 г. Бойль установил, что при постоянной температуре газа (независимо от ее величины) остается неизменным и произведение p*V. Если же газ нагревать или охлаждать, то значение p*V соответственно увеличивается или уменьшается. Как видно из уравнения (3.3), p*V пропорционально кинетической энергии молекулы, отсюда мы легко можем установить связь между энергией и температурой. Следовательно, мы подошли к определению температуры через свойства идеального газа. Таким образом, температура прямо пропорциональна кинетической энергии молекул:

Это простейшее соотношение между E и T. Для определения величины T в уравнение (3.3) подставим значение E, полученное из (3.4):

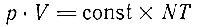
или

Значение постоянной k (одной из основных физических констант) зависит от того, в каких единицах мы измеряем p, V и T. Она была введена австрийским физиком Больцманом (1844-1906) и в честь него получила название постоянной Больцмана.

Величина кинетической энергии молекулы идеального газа равна ^3k*T/₂. Причем, как показывает кинетическая теория газов, эта величина не зависит от природы частиц, из которых состоит газ. В нашем примере мы говорили о молекулах, но это могут быть и атомы, и даже элементарные частицы, например электроны. Итак, независимо от природы частиц их энергия при одной и той же температуре одинакова. Она зависит только от их массы. Мерой относительной массы молекул служит так называемый молекулярный вес M₁ (это масса m какой-либо молекулы, отнесенная к эталонной массе, в качестве которой выбран вес атома углерода, равный 12). Тогда масса молекулы определяется из соотношения

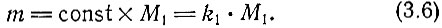
Общая масса M газа в сосуде равна N*m, или k₁*N*M₁, а число молекул равно 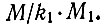Тогда уравнение (3.3) принимает вид

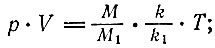
видоизменив его, получаем

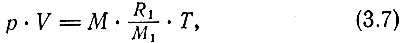
где R₁ - новая константа, называемая универсальной газовой постоянной.

Уравнение (3.7) называют уравнением состояния идеального газа. С его помощью мы можем определять цифровое значение температуры. Из уравнения (3.7) находим, что при определенной массе газа в закрытом сосуде постоянного объема температура пропорциональна давлению. Другими словами, если при давлении p₁ температура равна T₁, то давлению p соответствует температура T, то есть

Следует отметить, что описываемая этим соотношением закономерность была экспериментально установлена Чарлзом (1787).

Температура, равная 273,16 K по шкале Кельвина, есть температура, при которой воспроизводится физическое состояние, известное под названием тройственная точка воды. Уравнение (3.8) можно использовать для калибровки газового термометра, при этом нужно просто для каждого значения температуры измерять давление, что сравнительно нетрудно. Постоянную (_T1/_p1) можно выбирать произвольно; но наиболее удобно использовать отношение 273,16 K на 1 атм, так как при атмосферном давлении по этой шкале точки замерзания и кипения воды отстоят друг от друга также на 100 градусов, как и по стоградусной шкале Цельсия. В нашей книге мы будем пользоваться значениями температуры, измеренными по шкале Кельвина [она названа так в честь английского физика Уильяма Томсона, позднее лорда Кельвина (1824-1907)] с помощью термометра на основе идеального газа.