Коэффициент полезного действия циклических процессов

Цель наших, исследований состоит в том, чтобы оценить, какое количество солнечной энергии можно превратить в работу, если использовать эту энергию для приведения в действие тепловой машины.

Если снова обратиться к нашему простому циклу, то можно сразу заметить, что ограничения, обусловленные вторым началом термодинамики, снижают эффективность цикла. Тепловая энергия Q₁ поступает от источника, а Q₂ - передается охладителю, который, имея низкую температуру, не может выполнять функцию источника в следующем цикле. Если количество энергии Q₂, составляющее некоторую часть от Q₁, безвозвратно теряется, то полезное количество энергии равно Q₁ - Q₂ и, следовательно, коэффициент полезного действия (к. п. д.) η определится отношением полезной энергии ко всей затраченной, то есть

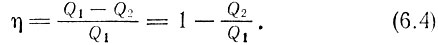
Одновременно заметим, что полезная работа, совершенная за цикл, равна W₁ - W₂, поэтому к. п. д. можно также записать в виде

Необходимо еще раз подчеркнуть, что снижение эффективности цикла заложено в самой сути вещей и не связано с недостатками механизмов, используемых для его практической реализации. Тогда интересно узнать, каково, с учетом указанных ограничений, наивысшее из возможных значение к. п. д., соответствующее наиболее "совершенной" машине. Установлено, что такая машина должна обладать свойством обратимости. Рис. 38 помогает понять сущность этого свойства. Если изображенной в левой части рисунка машине дать обратный ход, то направления всех потоков энергии в ней изменятся на противоположные. В этом случае машина будет приводиться в действие работой, а получаемая тепловая энергия поступать от охладителя к источнику. Подобные процессы осуществляются в рефрижераторе или тепловом насосе, которые мы рассмотрим позднее. Нетрудно показать, что такая обратимая машина является самой эффективной из всех возможных. Предположим, что в качестве привода для нашей машины, работающей в обратимом режиме, используется еще более эффективная машина, изображенная на рис. 39. Для получения работы W эта сверхэффективная машина должна отбирать от источника энергию 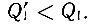Следовательно, отдаваемая в этом случае охладителю энергия, равная также оказывается меньше, чем аналогичная величина для обратимой машины. 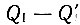Тогда полная энергия, полученная от охладителя, составляет и энергия, отданная источнику, также равна 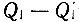следовательно, общее количество работы равно 0. Если бы нечто подобное могло произойти, то это означало бы нарушение второго начала термодинамики в формулировке Клаузиуса, то есть энергия 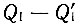передавалась бы от холодного тела к горячему без вмешательства извне. Отсюда следует вывод, что более эффективной машины, чем обратимая, не может быть.

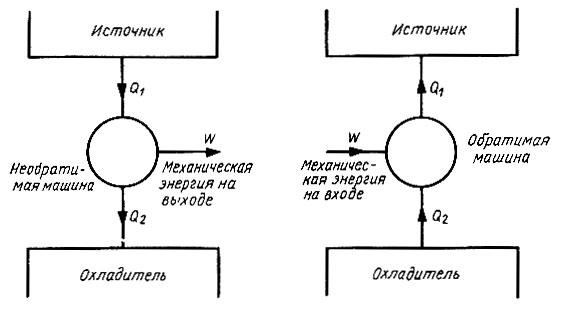
Рис. 38. Потоки энергии в тепловой машине

Поскольку наша идеальная машина ничем другим не отличается, кроме того, что она обратимая, можно заключить, что все обратимые машины, работающие между источником и охладителем, одинаково эффективны, независимо от принципа их действия, рабочего вещества и т. п. От чего же зависит к. п. д. идеальной машины? Другими параметрами, характеризующими подобные системы, являются лишь температуры источника и охладителя, следовательно, к. п. д. идеальной обратимой машины зависит лишь от их величин. Тогда мы можем записать следующее соотношение, вытекающее из (6.4):

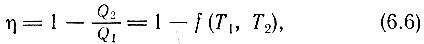
где f(T₁, T₂) есть некоторая функция от T₁ и T₂, вид которой мы еще не определили. Теперь рассмотрим устройство, схематически изображенное на рис. 40.

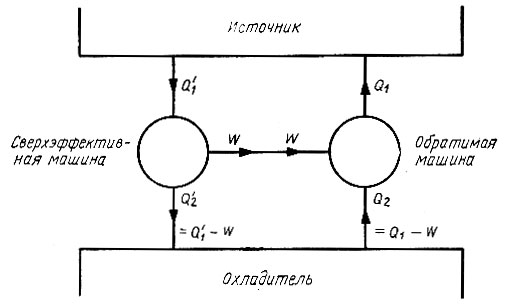
Рис. 39. Гипотетическая 'сверхэффективная' машина

Две обратимые машины работают от трех источников. Если эту систему выполнить так, чтобы нижняя машина отбирала от источника точно такое же количество энергии, сколько верхняя машина ему отдает, то такая система оказывается эквивалентной единственной обратимой машине, общая производительность которой составляет (Q₁ - Q₃) + (Q₃ - Q₂), что равно Q₁ - Q₂. Тогда уравнение (6.6) для каждой из машин можно записать в виде

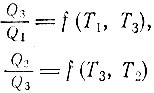
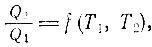
где функция f в каждом случае должна иметь один и тот же вид. Далее, поскольку ^Q₂/_Q1 = ^Q₂/_Q3*^Q₃/_Q1, то функция f должна удовлетворять соотношению

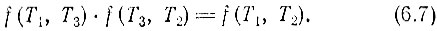
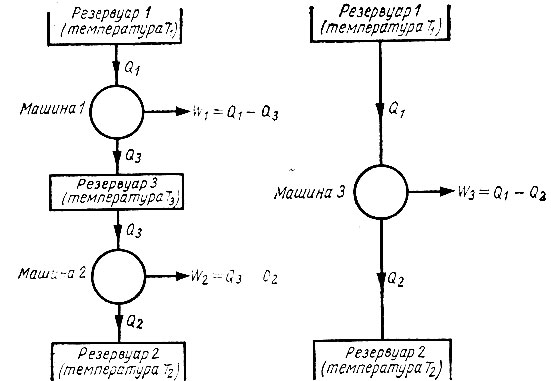
Рис. 40. Система на основе тепловых машин

Как известно, уравнению (6.7) удовлетворяют несколько функций. Простейшей из них (которая применима и для других термодинамических рассмотрений) является следующая:

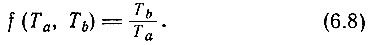
Тогда уравнение (6.7) принимает вид

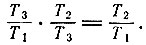
Таким образом, в своем исследовании мы подошли к самому важному соотношению. На основе уравнений (6.6) и (6.8) мы установили, что к. п. д. любого двигателя, использующего теплообмен с источником и охладителем, определяется уравнением

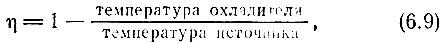
а соотношение между энергиями источника и охладителя определяется равенством

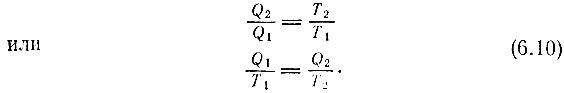
К. п. д., выраженный уравнением (6.9), иногда называют к. п. д. цикла Карно.

Уравнение (6.9) позволяет понять суть ограничений, накладываемых самой природой на работу тепловых машин. К. п. д. машины можно увеличить путем повышения температуры источника или понижения температуры охладителя. Однако здесь наши возможности не беспредельны. С одной стороны, температура источника ограничивается предельной температурой, которую может выдержать его материал, с другой стороны, в природе не существует каких-либо "вечных" охладителей, температура которых была бы значительно ниже атмосферной. Поэтому на практике в качестве охладителей обычно широко используют либо непосредственно воздух, либо воду различных водоемов (рек, морей и т. п.).