Распределение электронов по энергиям

Электроны зоны проводимости способны свободно (двигаться в твердом теле и являются носителями тока. Энергия таких электронов вследствие их взаимодействия друг с другом и с колеблющимися ионами непрерывно меняется небольшими порциями. В результате обмена электронами между уровнями в какой-то момент наступает устойчивое распределение электронов по энергетическим уровням, соответствующее равновесному состоянию. Нам важно понять, каково распределение электронов на самых высоких энергетических уровнях. Расчет истинного распределения электронов требует сложного статистического подхода, которым мы не будем здесь пользоваться. Мы поясним, как происходит это распределение на простом примере с парой игральных костей. Очевидно, здесь возможны одиннадцать различных сочетаний от 2 до 12. Но если кости бросать много раз, некоторые сочетания наблюдаются чаще других. Пусть, например, это будет цифра 7. Ее можно получить из большего числа комбинаций, чем какое-либо другое число (цифра 7 может складываться из 1 и 6, 2 и 5, 3 и 4, 4 и 3, 5 и 2, 6 и 1, тогда как, например, цифру 3 можно получить только из сочетания 1 и 2, а также 2 и 1). Бросая кости достаточно много раз, подсчитывая количество случаев появления каждого из возможных чисел,- мы в итоге получим распределение по разрешенным сочетаниям. Читатель может убедиться в том, что различные сочетания костей можно составить 36 различными способами, 6 из них дают нам цифру 7, цифру 3 можно получить лишь 2 способами. Из рис. 56 мы видим, что доля от общего числа бросков, приходящаяся на каждое из возможных сочетаний, составляет ⁶/₃₆ для 7, ²/₃₆ для 3 и т. д. Итак, при огромном числе бросков пар костей распределение сочетаний в какой-то момент принимает вид, показанный на рис. 56. Та же картина наблюдается и в любой другой момент, хотя сами сочетания пар костей изменяются. Подобным же образом можно представить и распределение электронов по разрешенным энергетическим уровням, хотя на него накладываются различные ограничения.

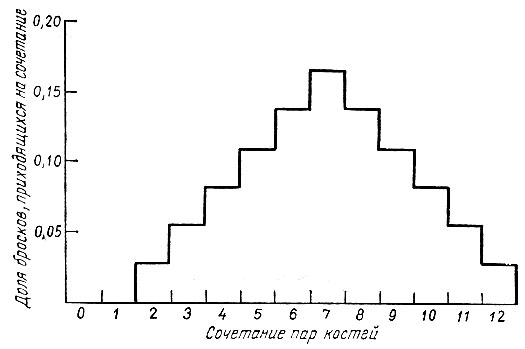
Рис. 56. Распределение сочетаний пар костей при многократном бросании

Для хороших электрических проводников энергетическое распределение получено в 1926 г. Ферми и Дираком, и поэтому оно известно как распределение Ферми-Дирака (рис. 57). Число отдельных энергетических уровней здесь столь велико, - что заметить ступенчатый характер распределения, как в случае игральных костей, невозможно. Ступени так малы, что переходят в непрерывную кривую. На рис. 57 по вертикали отложена доля электронов, энергии которых лежат в узкой области в окрестности величины E. Приведенная кривая описывается уравнением

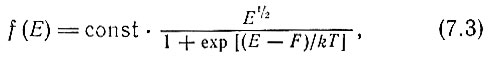
где kT имеет тот же смысл, что и в уравнении (3.4), определяющем кинетическую энергию частицы при температуре T. Читатель, не знакомый со свойствами экспоненциальной функции, представленной в знаменателе уравнения (7.3), может понять их из графика. За исключением зоны щириной в несколько kT, лежащей вблизи значения энергии F, названной уровнем Ферми, распределение слабо зависит от температуры. Но вблизи F концентрация электронов резко падает с повышением температуры. Повышение температуры само по себе оказывает незначительное влияние на энергию электронов (так, для металлов при нормальной температуре kT близко к ¹/₂₀₀ F а при T = 1000 K, kT ≈ (¹/₇₀ F), но с ростом температуры все больше электронов имеют энергию выше уровня Ферми и меньше - энергию ниже F.

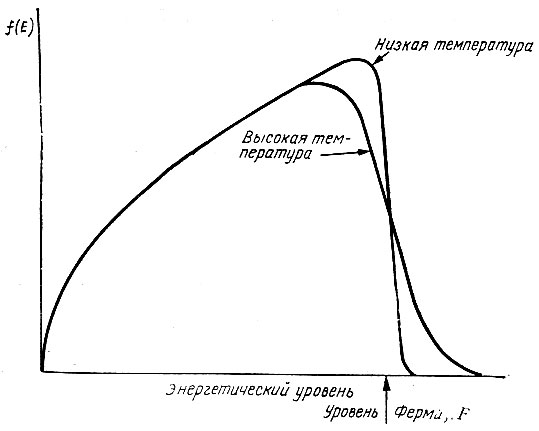
Рис. 57. Распределение Ферми - Дирака

Теперь мы уже можем рассмотреть принцип действия первого устройства для преобразования теплоты в электричество. Однако прежде мы введем еще одну единицу энергии, называемую электронвольтом (эВ). Для характеристики энергий на атомном уровне такая единица, как джоуль, оказывается слишком большой. Например, кинетическая энергия электрона при обычной температуре составляет всего лишь около 4*10^-21 Дж. Электронвольт - значительно меньшая единица. 1 эВ равен работе, которую необходимо совершить, чтобы переместить электрон между двумя точками с разностью потенциалов 1 В (вольт). Очевидно, эта единица более подходит для нашего обсуждения. Соотношение между джоулем и электрон-вольтом легко получить. 1 Дж соответствует работе, выполняемой при мощности 1 Вт в течение 1 с. Мощность в 1 Вт выделяется, например, при прохождении тока в 1 А (ампер) в проводнике под действием разности потенциалов в 1 В. Току в 1 А соответствует скорость протекания заряда 1 ^Кл/_с, или 6,25*10^18э/_с. Следовательно, 1 Дж = 1 Вт*с = 1 A*B*c = 6,25*10¹⁸*^э/_с*B*c = 6,25*10¹⁶ эВ или 1 эВ = 1,6*10^-19 Дж.

Постоянную k мы впервые ввели при рассмотрении основ кинетической теории (см. гл. 3). Она называется, как уже говорилось, постоянной Больцмана и равна ¹/₁₁₆₀₀ эВ*K. Следовательно, kT при обычных температурах (T = 300 K) составляет около 0,026 эВ, а при T = 1000 K примерно 0,086 эВ. Для сравнения укажем, что уровни Ферми обычно лежат в диапазоне от 5 до 10 эВ.

Теперь, познакомившись с понятием электронных энергетических уровней и соответствующей единицей энергии, мы обратимся к первому типу устройств для прямого генерирования электрической энергии - термоионному генератору. Этот прибор разработан в последние десятилетия, и ему принадлежит исключительно важная роль при производстве электроэнергии в будущем. Широкому читателю он малоизвестен, поэтому мы считаем целесообразным познакомиться с ним более детально.