Термоэмиссия

Хотя число свободных электронов в проводнике велико, тем не менее, как показывает опыт, они "неохотно" покидают его поверхность. Это можно легко объяснить, если проанализировать поведение отдельного электрона в изолированном образце металла. Пока электроны остаются в твердом теле, оно электронейтрально, поскольку содержит равное число электронов и ионов. При испускании электрона в теле возникает дефицит отрицательного, или избыток положительного заряда. Этот избыточный положительный заряд не обязательно сосредоточен в какой-то определенной точке тела, но для любого данного положен ния электрона вне тела распределение заряда внутри тела можно считать таковым, как если бы положительный заряд был сосредоточен в некоторой особой точке. Эта воображаемая точка показана на рис. 59.

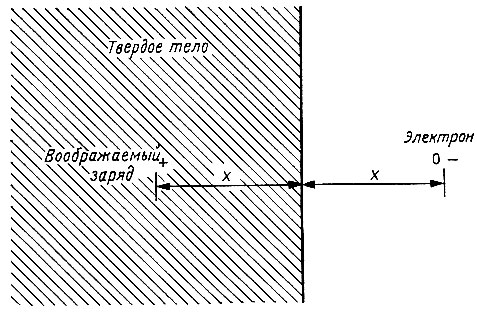
Рис. 59. К объяснению механизма электронной эмиссии

Притяжение электрона твердым телом определяется силой кулоновского взаимодействия между, разноименными зарядами, находящимися на расстоянии 2x друг от друга:

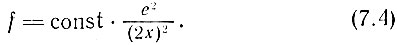
В этом уравнении точное значение x неизвестно, поскольку с точки зрения атомной структуры поверхность твердого тела нельзя считать гладкой (как показано на рисунке), и мы не в состоянии с уверенностью указать местоположение воображаемой точки! Однако мы можем оценить работу, которую нужно было бы совершить, чтобы переместить электрон с поверхности тела в направлении, противоположном действию этой уменьшающейся с расстоянием кулоновской силы. Работу по перемещению электрона за пределы тела называют работой выхода φ. Ее можно приблизительно подсчитать с помощью уравнения (7.4). Поскольку препятствующая перемещению электрона сила резко падает с увеличением расстояния, ее действие можно учесть в виде небольшой добавки к величине работы по перемещению электрона после того, как он отделен от поверхности тела более чем на несколько микрометров. Таким образом, работа выхода приблизительно равна кинетической энергии, которую должен приобрести электрон, находящийся внутри тела, чтобы покинуть последнее. Для металлов работа выхода составляет 2-5 эВ. Поскольку это значительно превышает величину kT при обычных температурах, то на основании выводов, сделанных в предыдущем разделе, мы можем заключить, что при обычных температурах электроны не в состоянии покинуть поверхность металла, что и соответствует действительности.

При повышении температуры тела электроны приобретают энергию, близкую к энергии уровня Ферми. Следовательно, величину φ можно рассматривать как дополнительную энергию, которая необходима электрону для выхода за пределы твердого тела из положения, соответствующего уровню Ферми F. Из уравнения Ферми - Дирака (7.3) для распределения электронов по энергиям видно, что число электронов с энергией, равной или превышающей F + φ, пропорционально T²exp(^-φ/_kT). Тогда зависимость числа электронов, вылетающих с единицы поверхности в единицу времени, от температуры T определяется уравнением

где A - постоянная. Поскольку полный поток электронов есть не что иное, как ток, то j характеризует плотность тока. Уравнение (7. 5) известно как уравнение Ричардсона (первые исследования термоэмиссии "Ричардсон осуществил в 1903 г.). Величина A - некоторая универсальная постоянная, приблизительно равная 1,2*10^6A/_м²*K². Оказывается, что процесс электронной эмиссии с поверхности твердых тел очень похож на испарение жидкости, которое мы кратко рассмотрели в гл. 5. При испарении также необходимо затратить работу на отделение молекулы от окружающих ее молекул жидкости, и доля молекул, обладающих достаточной для этого энергией, с повышением температуры резко увеличивается. Итак, эмиссионный ток, от которого зависит работа термоэмиссионного генератора, изменяется с температурой. В табл. 3 приведены значения плотности эмиссионного тока при различных температурах для типичных электродов из вольфрама с цезиевым покрытием и без него, а также из окиси серебра с цезиевым покрытием, работа выхода которых равна 2; 4,5 и 1 эВ соответственно.

Таблица 3. Плотность тока термоэмиссии (^A/_м²) при различных температурах

Эта таблица наглядно показывает, насколько сильно эмиссия зависит от работы выхода при данной температуре и как с повышением температуры плотность термоэмиссионного тока растет (до величины порядка 10^5A/_м²). Однако рост температуры ограничен двумя факторами. Во-первых, при значительном увеличении плотности тока внутренние потери на сопротивление, или джоулевы потери, становятся чрезвычайно большими. Во-вторых, при слишком высокой температуре положительные ионы сами приобретают энергию, достаточную, чтобы покинуть кристаллическую решетку, и тогда возникают потери вещества в результате "испарения". Позже мы рассмотрим и другие факторы, определяющие выбор материалов электрода.