2. Симметрия и асимметрия в неживой природе

Наиболее полно вопросы симметрии для неживой природы рассмотрены в кристаллографии. Правильность внешней формы кристаллов давно обратила на себя внимание естествоиспытателей и философов. По мере накопления знаний о природе усиливалось стремление найти причины, порождающие те или иные явления в окружающем мире. В числе других вопросов изучалась и симметрия кристаллов, но прошло много веков, прежде чем в конце XVIII в. (1783 г.) французский ученый Роме де Л'Иль открыл один из важнейших законов кристаллографии - закон постоянства двугранных углов в кристаллах, состоящий в том, что углы между соответственными гранями во всех кристаллах одного и того же вещества являются постоянными. Здесь очень важно отметить, что Роме де Л'Иль, изучая углы единичных кристаллов, поднялся до уровня высокого научного обобщения, распространив закон постоянства углов на кристаллы всех веществ.

Французский ученый Р. Ж. Гаюи своими работами по геометрической кристаллографии продолжил работы Роме де Л'Иля и открыл очень важный закон - закон целых чисел, который, без сомнения, оказал влияние и на открытие Дальтоном закона целых чисел в химии. Если Роме де Л'Иль считал, что природа скрыла от нас внутреннюю сущность кристаллов и она непознаваема, то Р. Ж. Гаюи исходя из материалистической точки зрения дал объяснение сущности закона целых чисел и создал теорию внутреннего строения кристаллов из многогранных молекул. Опираясь на опытный факт, заключающийся в том, что при дроблении кристалла, например каменной соли, его осколки имеют правильную форму параллелепипедов, он пришел к выводу, что молекулы каменной соли должны иметь такую же форму. Хотя его представления о форме молекул не имеют ничего общего с действительностью, но идея о молекулярном строении вещества была основой открытого им закона целых чисел и тем самым получила опытное подтверждение.

В 1819 г. Э. Митчерлихом было обнаружено, что близкие по составу вещества кристаллизуются в одинаковых формах, которые были названы им "равноформенными", т. е. изоморфными.

Тремя годами позже (в 1822 г.) Э. Митчерлих открыл явление полиморфизма, заключающееся в том, что некоторые вещества в различных условиях способны образовывать разные по симметрии и форме кристаллы. Различие в пространственном расположении одних и тех же атомов, различные типы кристаллических решеток (графит - гексагональная, алмаз - кубическая), составленных из одних и тех же атомов, приводят к существованию полиморфных модификаций, часто резко отличающихся друг от друга по своим физическим свойствам.

Явления изоморфизма и полиморфизма имеют глубокий философский смысл. Они - одно из многочисленных проявлений действия закона перехода количественных изменений в качественные. Здесь имеет место дальнейшее обогащение содержания категории количества, так как в него включается не только изменение числа элементов, частей, составляющих целое, но и изменение пространственного расположения этих частей.

Одним из основных свойств кристаллов является анизотропия - неравносвойственность, т. е. изменение свойств в зависимости от направления. Вместе с тем кристаллы являются телами однородными. Это означает, что два участка кристалла одинаковой формы и одинаковой ориентировки одинаковы по своим свойствам.

Исследование кристаллов привело к установлению интересного (прежде всего для философов-марксистов) их свойства, а именно: один и тот же кристалл может быть одновременно анизотропным и изотропным, прерывным и непрерывным в отношении различных его свойств, т. е. в одном и том же кристалле мы наблюдаем наличие противоречивых, исключающих друг друга свойств. А. В. Шубников показал, что это противоречие логически необходимо. Так, например, все кристаллы кубической системы, будучи явным образом анизотропными в отношении ряда свойств (упругость, прочность и т. д.), являются изотропными в отношении термического расширения. Все кристаллы кубической системы в отношении теплового расширения имеют симметрию шара. В заключение своей статьи А. В. Шубников справедливо указывает: "...симметрия и дисимметрия, изотропия и анизотропия, прерывность и непрерывность кристаллов суть свойства относительные. Не существует симметрии кристаллов "вообще", а существует симметрия кристаллов в отношении тех или иных его свойств; не существует анизотропии кристаллов "вообще", а существует анизотропия кристаллов в отношении некоторых его свойств; не существует прерывного (решетчатого) строения кристаллов "вообще", а существует прерывное строение в отношении определенных его свойств" (147. 1951.44(1), 6).

Одни и те же по составу и форме молекулы могут быть "упакованы" в кристалле разными способами, от этого зависят физико-химические свойства вещества.

В 1813 г. английский ученый Волластон выступил с идеей шарообразных молекул, которые в пределе изображались как математические точки. Упорядоченное расположение этих точек в пространстве привело к возникновению понятия пространственной кристаллической решетки, понятия симметрии решеток.

Решетку кристалла следует понимать как математическую абстракцию такого же типа, как и понятие элемента симметрии, с которым мы имеем дело при изучении, скажем, внешней формы кристалла. Эта математическая абстракция дает возможность описывать периодичность кристаллической структуры. Следовательно, структура - это конкретное расположение материальных частиц в кристалле, а понятие "кристаллическая решетка" - только математический образ этой структуры. Роль этой абстракции, как и других математических абстракций в познании законов природы, исключительно велика. Так, было установлено на опыте, что в кристаллах не встречаются оси симметрии 5-го, 7-го и более высоких порядков. В течение длительного времени этот опытный факт не находил объяснения. Введение понятия решетки кристалла в качестве одного из следствий привело к объяснению вышеназванного опытного факта. Поскольку решетка есть бесконечное, трехмерное периодическое образование и это основное свойство проявляется в том, что любые ее два узла можно совместить друг с другом при помощи переноса, причем все остальные узлы совместятся со всеми другими узлами, а в целом вся решетка совместится сама с собой, исходя из этого доказывается и невозможность существования в кристаллах осей 5-го, 7-го и высших порядков.

Симметрия проявляется во внешней форме кристаллов, в физических явлениях, протекающих в них, во взаимодействии кристаллов с окружающей средой, в изменениях, претерпеваемых кристаллами под влиянием внешних воздействий.

Законы симметрии относятся не только к внешней форме кристаллов - им подчинено и их внутреннее строение. Внешняя форма- это проявление внутреннего строения кристаллов.

В 1830 г. Иоганн Фридрих Христиан Гессель на основе применения закона рациональности дал геометрическое доказательство того, что в природе существует только 32 класса кристаллов. Но на его работу не обратили внимания и случилось так, что эта систематика была вновь открыта в 1867 г. русским ученым А. Гадолиным.

Внутреннее строение кристалла дает значительно большее разнообразие элементов симметрии, чем его внешняя форма. Это нашло свое отражение в выведенных в 1890 г. выдающимся русским ученым Е. С. Федоровым всех возможных сочетаний элементов симметрии в пространстве; причем он доказал, что число таких пространственных групп симметрии равно 230. С помощью математического предвидения Федоров как бы пересчитал, проинвентаризировал все существующие пространственные решетки задолго до того, как рентгеноструктурный анализ подтвердил истинность этих расчетов. Это было величайшим достижением науки. Опытная проверка теории Федорова привела к блестящему ее подтверждению. До сих пор не найдено ни одной формы кристалла, которая не принадлежала бы к той или иной федоровской группе.

Большой вклад в кристаллографию и особенно в учение о симметрии внес Пьер Кюри. В своих работах по симметрии, опираясь на труды видного французского математика М. Э. Жордона, и в частности на его работу "О группах движений" (1867), в которой этот ученый опубликовал полный список всех систем обычных осей, или осей, допускающих повторность по винтовой линии, характерных для неограниченных сред, он показал, что эта система в сочетании с типами симметрии для кристаллических сред дает возможность получить "то расположение, которое дают Зонке, Федоров, Шенфлис". П. Кюри писал, что "каждый физик ежедневно пользуется в более или менее явной форме понятиями симметрии" (209, 148). Он считал необходимым, чтобы в физику было введено понятие симметрии, столь обычное и полезное в кристаллографии. П. Кюри подчеркивал, что физики "часто пользуются условиями симметрии, но обычно пренебрегают определением симметрии в тех или иных явлениях, потому что довольно часто условия симметрии в них просты и почти очевидны a priori" (209, 149).

М. Кюри в своих воспоминаниях писала о том, что Пьер Кюри очень интересовался физикой кристаллов. Его теоретические и экспериментальные исследования в этой области группировались вокруг общего принципа - принципа симметрии; он выяснил его мало-помалу, и окончательная формулировка была дана им лишь в статьях, напечатанных в течение 1893-1895 гг.

Вот эти формулировки, ставшие с тех пор классическими: "Когда определенные причины порождают известные следствия, элементы симметрии причин должны вновь появиться в порожденных следствиях..."

"Когда известные следствия имеют в себе известную дисимметрию, эта последняя должна находиться и в породивших явление причинах".

"Положения, обратные двум предыдущим, неправильны, по крайней мере, на практике, т. е. следствия могут быть симметричнее вызвавших их причин..."

"Большое значение этого закона, совершенного по своей простоте,- писала М. Кюри,- заключается в том, что в нем трактуются элементы симметрии, относящиеся ко всем без исключения физическим явлениям".

Основываясь на глубоком изучении групп симметрии, которые могут существовать в природе, Пьер Кюри показал, как нужно использовать эти факты и с геометрической, и с физической точек зрения, чтобы предвидеть возможность или невозможность появления данного феномена в условиях опыта.

Принцип симметрии, так живо интересовавший ум Пьера Кюри, является одним из тех немногочисленных великих принципов, которые господствуют в физических явлениях; исходя из понятий, вытекающих из опыта, они мало-помалу приобретают все более и более совершенную форму (68, 24-25).

В науке наряду с симметрией уже давно пользовались понятиями асимметрии и дисимметрии, но часто рассматривали их как случайное нарушение симметрии, т. е. симметрия, асимметрия и дисимметрия рассматривались в отрыве друг от друга, хотя были отдельные попытки рассматривать их и в единстве.

Термин "дисимметрия" имеет широкое распространение в кристаллографической, химической и физической литературе. Впервые он был, по-видимому, введен в науку Л. Пастером, который под дисимметрией понимал свойство определенных фигур не совмещаться простым наложением со своим зеркальным изображением. Примером таких фигур может служить фигура руки человека: известно, что фигура правой руки не может быть совмещена простым наложением со своим зеркальным изображением, т. е. с фигурой левой руки. В настоящее время мы можем определить дисимметрию Л. Пастера как отсутствие в фигуре элементов симметрии второго рода; им отвечают операции симметрии, эквивалентные нечетному числу отражений в плоскостях (простое отражение в одной плоскости, инверсия, зеркальные повороты, скользящие отражения).

Понятие дисимметрии у Пьера Кюри гораздо шире. Под дисимметрией он понимал совокупность всех элементов симметрии, отсутствующих в фигуре. Очень важно отметить следующее существенное различие между симметрией и дисимметрией. Известно, что полная совокупность операций симметрии, отвечающих всем присутствующим в фигуре элементам симметрии, образует группу в математическом смысле. Это означает, что произведение любых двух операций группы эквивалентно по результатам какой-либо одной операции той же группы. В противоположность этому полная совокупность операций симметрии, отвечающих всем отсутствующим в фигуре элементам симметрии, не образует группы в математическом смысле. По Пьеру Кюри, для предсказания новых явлений дисимметрия более существенна, чем симметрия. Поскольку, однако, замечает он, число отсутствующих элементов симметрии всегда бесконечно велико, проще перечислять элементы симметрии (присутствующие), чем элементы дисимметрии (отсутствующие элементы симметрии). Кратко точку зрения П. Кюри на дисимметрию можно сформулировать так: дисимметрия творит явление.

Обычно кристаллы рассматриваются как наиболее правильно построенные тела. В действительности строение кристаллов значительно сложнее.

Изучение строения кристаллов привело к открытию очень важного для теории и практики явления так называемого зацепления, или дислокации. Модельное представление о дислокации состоит в следующем: если между двумя прозрачными пластинками из пластмассы поместить много незакрепленных стальных шариков и встряхнуть эту систему, то шарики стремятся расположиться так, чтобы получилась "кристаллическая решетка". Но в этой "решетке" часто наблюдаются дефекты двух видов: пустоты, или вакантные места, и дислокации, т. е. смещения рядов шариков относительно друг друга, ведущие к росту "рыхлости" решетки.

Частицы кристалла совершают сложные и разнообразные движения около своих положений равновесия. Размах тепловых колебаний довольно велик. Даже при комнатной температуре он составляет 0,1-0,2 ангстрема, т. е. несколько процентов от величины периода, через который повторяется кристаллическая структура.

Идеальный кристалл представляет собой трехмерную бесконечную решетку, элементы которой периодически повторяются. Как показали исследования, реальные кристаллы имеют серьезные отклонения от этой идеальной структуры. Они как бы состоят из отдельных блоков, каждый из которых - это кусок идеальной (с определенной степенью приближения) решетки. Эти представления получили экспериментальное подтверждение в опытах по деформации кристаллов. Теория дислокации удовлетворительно объясняет явление сдвига кристаллических плоскостей при пластической деформации кристаллов, которая с современной точки зрения представляет собой движение беспорядка, нарушение симметрии вдоль кристалла.

В современной физике и химии большое внимание уделяется изучению элементов беспорядка в упорядоченной молекулярной постройке и, наоборот, исследованию элементов порядка в хаосе беспорядочного расположения частиц. Идеальный беспорядок мы называем изотропией. Так, например, беспорядочное движение молекул газа проявляется в том, что в любом направлении движется одинаковое число молекул и что большинство молекул имеет скорость, близкую к средней. В интересной работе А. И. Китайгородского "Порядок и беспорядок в мире атомов" показано, что существуют элементы порядка в беспорядке, элементы беспорядка в порядке, переходы порядок ⇔ беспорядок. Так, например, фазовые превращения - это переходы порядка в расположении атомов в беспорядок или обратно.

Наиболее вероятным распределением молекул является беспорядок как в отношении расположения, так и в отношении скоростей. Но такое положение имеет место при отсутствии сил, действующих на частицы. Эти силы действуют в направлении установления порядка, идет "борьба" порядка с беспорядком. "Борьбу" порядка с беспорядком можно проследить на множестве примеров, которые приводятся в вышеназванной работе А. И. Китайгородского. Таким образом, кристалл "живет" и сущность этой жизни состоит в непрерывной "борьбе" симметрии и асимметрии, порядка и беспорядка.

Мы указывали на то, что кристаллическая решетка состоит из блоков, по границам которых движутся зацепления (дислокации), и что блоки - это куски идеальной решетки. Но это представление об идеальной симметрии блоков также требует уточнения. Внутри блоков наблюдаются нарушения симметрии в форме пустых мест и примесей.

Даже незначительное наличие пустот и примесей оказывает существенное влияние на свойства кристалла.

Опыт показывает, что, скажем, добавление одного атома примеси на миллиард атомов германия существенно влияет на его проводимость.

Реальные кристаллы, из которых практически состоит вся неживая природа, представляют собой такое сочетание элементов (атомов, молекул, ионов), которое можно охарактеризовать как динамичное единство порядка и беспорядка, симметрии и асимметрии. По мнению А. И. Китайгородского, "Изучение элементов беспорядка в упорядоченной молекулярной постройке и, наоборот, исследование элементов порядка в хаосе беспорядочного расположения частиц привели к установлению новых важных закономерностей, связывающих строение вещества с его свойствами, объясняющих ряд явлений изменениями в степени упорядоченности структуры" (59, 3). Более глубокое проникновение в мир неживой природы привело физиков к более правильному отражению сущности объективной реальности, а это в свою очередь сделало более явственным диалектический характер происходящих там процессов.

Один из принципов симметрии - симметрия между левым и правым - давно уже выявлен человеком. Вопрос о том, проявляется ли в природе подобная симметрия, подробно обсуждался естествоиспытателями и философами как в прошлом, так и в настоящее время. Как известно, до 1957 г. в физике существовало твердое убеждение об однородном и изотопном пространстве. В связи с тем, что в этом пространстве все точки и направления равнозначны, казалось, что правое и левое - это относительные понятия. Опыты, подтвердившие несохранение четности при слабых взаимодействиях, породили сомнение в нерушимости наших представлений об однородности и изотопности пространства, а также об относительности понятий "правое" и "левое". Но еще задолго до этого вопросы, связанные с правизной и левизной, были предметом обсуждения среди ученых (22; 27, 930; 202).

Правое и левое являются относительными понятиями в том смысле, что безразлично, что назвать правым и что левым в момент установления этих понятий, но они в то же время и абсолютны, так как не являются тождественными, отличаются друг от друга. Условным, например, является то, что нейтрон мы называем частицей, а антинейтрон - античастицей; можно было бы назвать их и наоборот, так как, по существу, нейтрон и антинейтрон отличаются по своей спиральности (правый и левый винт).

Хотя в классической физике и использовался закон симметрии между правым и левым, однако большого практического значения эта симметрия не имела. Единственная причина этого заключается в том, что в отличие от симметрии относительно центра вращения, которая порождает непрерывное преобразование, симметрия между правым и левым порождает дискретное преобразование. В то время как непрерывное преобразование в классической механике всегда приводит к закону сохранения, дискретное преобразование к закону сохранения не приводит. Однако в рамках квантовой механики это различие между непрерывным и дискретным преобразованиями исчезает. Закон симметрии правого и левого также приводит к закону сохранения - закону сохранения четности.

Следует обратить внимание на то, что законы сохранения и связанные с ними симметрии в физике элементарных частиц часто нарушаются в одних и сохраняются в других взаимодействиях.

Инвариантность (неизменность) законов механики при переходе к равномерно движущейся системе координат (известная как инвариантность относительно преобразования Галилея) явилась примером первой лишенной простоты симметрии. Эта симметрия является одним из исходных принципов ньютоновской механики. Следствия, вытекающие из этого принципа симметрии, интенсивно разрабатывались физиками в прошлом веке и привели к ряду важных результатов.

В связи с созданием специальной и общей теории относительности законы симметрии приобрели новое значение: между законами симметрии и динамическими законами физики связь оказалась значительно более тесной и взаимоопределяющей, чем в классической механике. До появления квантовой механики принципы симметрии были распространены в физике не очень широко. Но теперь их значение резко возросло. Квантовые числа, которые характеризуют состояние системы, часто совпадают с квантовыми числами, определяющими ее симметрию.

Изучение атомных ядер привело к открытию зарядовой инвариантности и связанного с ней изотопического пространства. Изотопический спин частиц и ядер является сейчас не менее привычной характеристикой, чем обычный спин или заряд ядра.

До тех пор пока были известны две тяжелые частицы - протон и нейтрон, вопрос о новых квантовых числах не возникал; когда же были открыты гипероны, возник вопрос о том, в чем состоит причина их большой стабильности, так как время жизни 10-10 с по ядерным масштабам - очень большое время.

Первым шагом в построении теории, как и в истории теории атома, было введение "главного квантового числа" для системы уравнений барионов. Таким главным квантовым числом оказалась открытая Гелл-Манном и Нишиджимой странность S (или гиперзаряд Y, равный сумме S и барионного числа В).

Дальнейшее изучение этого вопроса показало, что открытие странности, несомненно, является одним из самых существенных этапов развития физики элементарных частиц.

Ученые на протяжении веков пользовались понятием симметрии и отмечали ее нарушения. Однако подлинная диалектическая связь симметрии и асимметрии оставалась нераскрытой.

Установление фактов нарушения симметрии, при отсутствии диалектического подхода к анализу этих фактов, часто приводит отдельных ученых к метафизическому противопоставлению симметрии асимметрии, к отрыву их друг от друга. В то же время ряд выдающихся естествоиспытателей чувствует неудовлетворенность односторонним подходом к симметрии, ее абсолютизацией, делает попытки более точно отразить законы объективного мира. Так, например, крупный американский физик-теоретик Е. Вигнер писал: "...приближенная точность законов симметрии - это общее явление и может стать общим законом. Мы напомним известную аксиому Э. Маха о том, что законы природы зависят от физического состава Вселенной, а физический состав Вселенной наверное не проявляет симметрии" (226, 265).

Есть все же основания предполагать, что именно отражение в теории существующих в действительности противоречивых тенденций симметрии и асимметрии приведет к ее более адекватному отражению.

До создания электродинамики, при господстве представлений механики Ньютона, внутренние свойства объектов рассматривались как изотропные. Объект, по этим представлениям, не содержал в себе каких-либо выделенных направлений, которые проявлялись бы во взаимодействиях. Такие объекты были наиболее бесструктурными и соответственно этому максимально симметричными в отношении своих внутренних свойств.

Создание электродинамики, а затем и теории относительности привело к тому, что во внутренних свойствах объектов были выделены направления, соответствующие направлению движения объекта.

Четырехмерный континуум не является вполне симметричным, так как в нем имеются направления, которые отличаются от других. Это так называемые нулевые направления, вдоль которых может распространяться свет. Как утверждает П. Дирак, "наша четырехмерная картина не является полностью симметричной. Тем не менее между четырьмя измерениями существует значительное число отношений симметрии" (31. 1963.12, 83). Рассмотрев существующие трудности теории гравитации, он приходит к выводу, "что четырехмерная симметрия не имеет такого (всеобщего.- В. Г.) значения и в некоторых случаях можно не учитывать ее..." (31. 1963.12, 84). П. Дирак не упоминает об асимметрии, но отсутствие элементов симметрии, неполная симметрия в данном случае и есть асимметрия.

Таким образом, 4-мерный пространственно-временной континуум представляет собой относительное единство симметрических и асимметрических элементов при ведущей роли симметрии.

Квантовая теория показала наличие асимметрии внутренних свойств элементарных частиц, которая связана с наличием спина, четности и других характеристик микрообъектов.

В связи с открытием несохранения четности Гелл-Манн и Фейнман показали, что для описания процессов распада, где четность не сохраняется, надо написать гамильтониан:

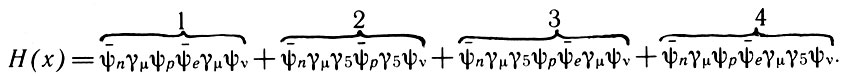
Такой гамильтониан называют аксиально-векторным, или V-А-взаимодействием.

Анализ этого гамильтониана указывает на то, что первые два слагаемых сохраняют четность, т. е. их можно назвать симметричными, а слагаемые 3 и 4 - асимметричными членами взаимодействия, поскольку при пространственном отражении они меняют знак. В данном случае индексы n, р, е, v характеризуют участвующие в распаде частицы - нейтроны, электроны, нейтрино; если в распаде будут участвовать другие частицы, то поменяются индексы при операторах соответствующих полей, но вид гамильтониана сохранится.

Было показано, что ни чисто симметричный, ни чисто асимметричный гамильтонианы не соответствуют действительности и только комбинация симметричных и асимметричных составных гамильтониана дает совпадение теории с экспериментом.

Продолжая наметившуюся тенденцию, можно предположить, что в развитии физики микромира будет возрастать роль асимметрии в познании внутренних свойств микрообъектов, но только в неразрывной связи с симметрией.

Отдавая должное такому мощному средству познания, как теория групп, мы в то же время должны отметить, что она в состоянии отобразить только свойства симметрии; причем таких форм симметрии, которые уже известны,- нужна лишь их математическая разработка.

На протяжении всей работы мы обращались к диалектическому единству симметрии и асимметрии и показали, что при исследовании неживой природы по мере углубления в микромир возрастает методологическая роль этого принципа, который находит свое частнонаучное воплощение в целой системе общих преобразований. Это прежде всего непрерывные преобразования пространства - времени (сдвиг систем как целого в пространстве, поворот в пространстве, сдвиг во времени, эквивалентность всех инерциальных систем отсчета); дискретные преобразования пространства-времени (пространственная инверсия Р обращение времени Т, зарядовое сопряжение С, комбинированная инверсия СР); преобразование внутренних симметрий (изотопическая инвариантность сильного взаимодействия, унитарная SUCS) симметрия, изотопическая инвариантность, унитарная симметрия по аромату кварков, цветовая симметрия, симметрия между кварками и лептонами, которая играет важную роль в создании единой теории, слабого, электромагнитного и сильного взаимодействии, суперсимметрия - симметрия, связывающая поля, кванты которых имеют целочисленный спин, с полями, кванты которых имеют полуцелый спин). Особое место в современной физике занимает калибровочная симметрия, которая свидетельствует о том, что некоторые сохраняющиеся физические величины (называемые "зарядами" - электрический заряд, гиперзаряд, "цвет" и др.) являются одновременно источниками полей. На основе калибровочной симметрии построены теории электрослабого и сильного взаимодействий. Известно, что массы промежуточных векторных бозонов W^± и Z° отличны от нуля. Этот феномен объясняют с помощью спонтанного нарушения симметрии (т. е. асимметрии); можно еще назвать такие формы симметрии, как киральная и др.

Следует иметь в виду, что в последнее время более широкое использование получают суперсимметрии, которые объединяя непрерывные (бозонные) и дискретные (фермионные) преобразования, выражают, по сути дела, моменты тождества между важнейшими видами материи - полем и веществом. Являясь частным случаем калибровочных симметрии, суперсимметрия приводит к образованию супермультиплетов, роль которых в классификации элементарных частиц хорошо известна. Суперсимметричное обобщение калибровочных полей Янга - Миллса позволяет объединить все компоненты электрического и слабого ядерного взаимодействий. Ставится также вопрос об объединении всех известных видов взаимодействий (включая гравитационное) путем восстановления нарушенной в процессах развития материального мира суперсимметрии.

Физика этих вопросов хорошо изложена в работах Янга, Генден-штейна, Криве, Эллиота, Добера, Барашенкова, Ахиезера и других; что же касается философских аспектов, то они рассмотрены значительно менее полно.