21. Совершали ли вы космический полет?

А Учебники астрономии и космонавтики утверждают, что в поле тяготения Земли тело летит по параболе только при условии, что его скорость равна второй космической (вблизи поверхности Земли вторая космическая скорость равна 11,2 ^км/_с). Если же скорость меньше, то тело движется по эллипсу, если больше - по гиперболе. Но вот мы бросаем камень - и он, как утверждают учебники физики, летит по параболе, хотя его скорость всего каких-нибудь 10 ^м/_с, т. е. в тысячу раз меньше второй космической. Как это объяснить?

Б Попробуйте рассмотреть, как полетел бы камень дальше, если бы ему не помешала поверхность Земли, т. е. если бы вся масса Земли была сосредоточена в ее центре.

В На рис. 15 показаны траектории тел, вылетевших с различными скоростями из точки Р, расположенной вблизи поверхности Земли. Скорость каждого тела в точке Р направлена горизонтально. Если скорость тела v такова, что центростремительное ускорение ^v2/_R равно ускорению свободного падения g, то тело движется по окружности В, центр которой совпадает с центром Земли. Из соотношения ^v2/_R = g находим, что нужная для этого скорость

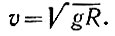
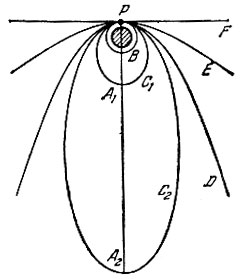
Рис. 15

У поверхности Земли g = 9,81 ^м/_с², R = 6380 км (радиус земного шара). Поэтому

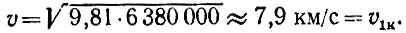
Эта скорость называется круговой или первой космической - это тот минимум скорости, который необходим, чтобы тело, брошенное горизонтально, не упало, а совершило полет вокруг Земли (и здесь и дальше мы не учитываем сопротивление воздуха).

Если скорость больше v_1к, то ускорение свободного падения не сумеет искривить траекторию до окружности. Кривизна траектории будет меньше, тело полетит по эллипсу (C₁ или С₂). Удаляясь от. Земли, тело израсходует избыток кинетической энергии на подъем. Достигнув максимального удаления (апогей, точка A₁ или A₂), тело начинает расходовать накопленную потенциальную энергию на увеличение своей скорости (на второй половине эллипса), возвращаясь к исходной точке Р, которая, таким образом, является перигеем орбиты.

Центр масс Земли находится в ближнем к точке старта фокусе эллипса. Второй фокус находится рядом с апогеем, на таком же расстоянии от А, на каком первый находится от перигея Р. Окружность является частным случаем эллипса, у которого оба фокуса совпадают. Чем больше скорость v по сравнению с v_1к, тем больше расходятся фокусы, тем сильнее вытянут эллипс. Наконец, при некоторой скорости v = v_2k второй фокус эллипса оказывается бесконечно далеко от Земли, т. е. орбита оказывается разомкнутой, имеющей форму параболы D. Скорость v_2k называется параболической, второй космической или скоростью убегания. Тело, ушедшее от Земли с такой скоростью, никогда не вернется обратно (если не вмешается какое-либо третье тело, например Луна).

Вторая космическая скорость ровно в √2 раз больше первой космической. У поверхности Земли

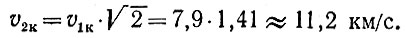
При скорости, превосходящей вторую космическую, тело движется по гиперболе Е, которая тем больше приближается к прямой F, чем выше скорость.

Рассмотрим теперь поведение тела при скорости, меньшей первой космической (круговой) v_1k. Пусть точка А (рис. 16) находится на большой высоте над Землей (чтобы тело могло падать). Допустим, что скорость тела чуть-чуть меньше первой космической. Тогда оно не сможет идти по круговой орбите и начнет с нее снижаться (G₁). Таким образом, точка старта А в этом случае является самой удаленной точкой орбиты, т. е. ее апогеем. Орбита G* также оказывается эллипсом, только теперь центр масс Земли находится в другом, более далеком от точки старта фокусе. Фокусы эллипса как бы поменялись ролями.

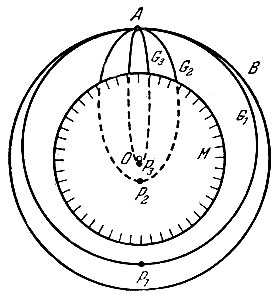
Рис. 16

С дальнейшим уменьшением стартовой скорости тела эллипс (G₂) начинает пересекать поверхность земного шара М, т. е. полет перестает быть космическим. Этого не произошло бы, если бы вся масса Земли была сосредоточена в ее центре. Чем меньше скорость тела в апогее A, тем ближе перигей Р к центру масс Земли. При обычных земных скоростях тел (десятки метров в секунду) перигей оказывается в непосредственной близости к центру, а эллипс - чрезвычайно сильно сплющенным.

Теперь можно сравнить траектории тел с v ≈ v_2k и v ≈ 0. Когда скорость тел мы увеличивали до второй космической, то эллипсы всё более и более вытягивались (C₁, С₂ и т. д. на рис. 15), пока не превратились в параболу. Примыкающая к точке старта часть эллипса, так же как и противоположная, тем меньше отличается от параболы D, чем ближе скорость тела к v_2к. Когда скорость тел мы уменьшали до нуля, то эллипсы всё более и более сплющивались (G₁, G₂ и т. д. на рис. 16), что для их формы равносильно вытягиванию. В результате примыкающая к точке старта часть эллипса опять оказывается все больше приближающейся к параболе. При скоростях 0-1000 ^м/_с часть траектории тела, проходящая над поверхностью Земли, практически совпадает с параболой.

В школьных учебниках параболичность траектории камня доказывается без участия законов Кеплера. Это доказательство справедливо, если в пределах всей траектории ускорение свободного падения постоянно по величине и направлению. В условиях полета камня или пули это в высшей степени правильно. Но уже снаряды дальнобойных орудий, а тем более ракеты летят в неоднородном поле тяжести (на пути в 111 км направление силы тяжести меняется на один градус), поэтому здесь уже приходится учитывать, что траектория является отрезком эллипса, в дальнем из фокусов которого находится центр масс Земли.

Интересно в связи с этим заметить, что с принципиальной точки зрения полет Валерия Брумеля над планкой при прыжке в высоту (как, впрочем, и каждого из вас) ничем существенным не отличается от космического полета. Прыгун, разбегаясь и отталкиваясь, выходит на эллиптическую орбиту, в одном из фокусов которой находится центр масс Земли. Во время выхода на орбиту (толчок) он, естественно, испытывает перегрузки. Зато на протяжении всего полета он испытывает самое настоящее (без всякой подделки!) состояние невесомости (если, конечно, пренебречь сопротивлением воздуха)^*).

^*) (Точно так же создается и невесомость в самолете, делающем "горку" по параболической траектории для тренировки космонавтов.)

Пройдя апогей своей орбиты (высшая точка над планкой), прыгун идет на снижение и, наконец, приземляется, подвергаясь при этом, как и полагается в конце космического полета, перегрузке. Единственное в этом смысле отличие полета Валерия Брумеля от полета Юрия Гагарина состоит в том, что у орбиты Гагарина и апогей и перигей находились вне Земли, в то время как у орбиты Брумеля над планетой находится лишь апогей, а перигей находится внутри планеты, что, естественно, мешает ему закончить полный виток вокруг Земли.