35. Гантель в космосе

А На Луне на тонкой прочной нити горизонтально подвешена "гантель" - стержень с двумя одинаковыми массами на концах (рис. 32, а). Точка подвеса совпадает с центром масс гантели. Отклоните слегка гантель от горизонтального положения (рис. 32, б) и отпустите ее. Какое положение примет гантель?

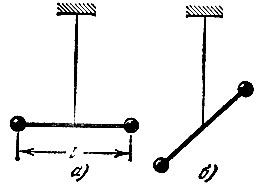
Рис. 32

Б Обычно отвечают так: поскольку центр масс совпадает с точкой подвеса, то гантель находится в безразличном равновесии. Следовательно, она останется в том положении, в которое мы ее установим: в наклонном, горизонтальном, вертикальном. И добавляют, что законы физики одинаковы на Луне и на Земле, а поэтому для постановки этого опыта не обязательно было забираться на Луну.

Согласен, этот опыт можно было бы поставить и на Земле, но только под колпаком, из-под которого откачан воздух, иначе движение воздуха могло бы раскачивать гантель и замаскировать те тонкие эффекты, которые должны проявиться в этой задаче. Таким образом, в задаче используется не столько Луна, сколько вакуум, существующий над ее поверхностью.

Теперь подсказка по существу задачи. Вес и масса - далеко не одно и то же: вес есть произведение массы на ускорение свободного падения. Обязательно ли центр тяжести совпадает с центром масс?

В В горизонтальном положении на две половинки гантели действовали одинаковые ускорения свободного падения (благодаря чему центр тяжести совпадал с центром масс), в наклонном - различные: в соответствии с законом всемирного тяготения Ньютона нижняя половина гантели будет тяжелее верхней, так как она ближе к центру Луны. В результате центр тяжести всей гантели сместится по стержню вниз от центра симметрии (а центр масс, всегда совпадающий с центром симметрии, останется на месте!), и стержень из наклонного положения начнет все быстрее и быстрее поворачиваться в вертикальное. С разгону он пройдет это положение, но затем затормозится и, совершив большое число колебаний, остановится вертикальном положении, когда энергия его колебаний израсходуется на трение о нить в точке подвеса. Вертикальное положение стержня будет положением устойчивого равновесия, так как центр тяжести займет самое низкое из всех возможных положений. Горизонтальное же положение было положением неустойчивого равновесия.

Вычислим разницу в силах, действующих на обе половины гантели в момент, когда ее стержень, имеющий длину l, уже установился вертикально. Будем полагать, что стержень невесом, а вся масса сосредоточена на его концах. Сила тяготения обратно пропорциональна квадрату расстояния от центра тяготения (в данном случае от центра Луны):

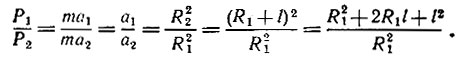
(1)

Здесь P₁ и P₂ - веса обеих половинок, а₁ и а₂ - их ускорения свободного падения, R₁ и R₂ - их расстояния от центра Луны.

Примем R₁ = 1750 км (несколько больше радиуса Луны) и длину стержня l = 100 м. Так как l << R₁, то третьим слагаемым в числителе формулы можно пренебречь по сравнению с первыми двумя. Тогда формула упрощается:

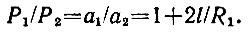
Поскольку и 2t << R₁, то, казалось бы, можно пренебречь и вторым слагаемым. Но если бы мы так сделали, то наша задача полностью исчезла бы: мы пришли бы к равенству Р₁ = Р₂ характеризующему однородное поле тяжести. Наша задача держится именно на наличии второго слагаемого, т. е. на том факте, что поле тяжести неоднородно. После подстановки численных значений l и R₁ имеем

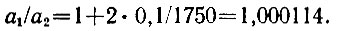
Разница в весе невелика (а в исходном наклонном положении она еще меньше), но в условиях вакуума и слабого трения нити этого достаточно, чтобы повернуть стержень в вертикальное положение.

На Земле (R₁ ≈ 6380 км) относительная разница в весе была бы еще меньше, хотя абсолютная (при одной и той же массе гантели) , была бы больше, чем на Луне. Интересно, что на Земле, в условиях наличия атмосферы, положением устойчивого равновесия было бы или вертикальное, или горизонтальное положение, в зависимости от плотности материала, из которого сделана гантель. Дело в том, что в этом случае пришлось бы принимать во внимание не только закон Ньютона, но и закон Архимеда. Поскольку плотность атмосферы Убывает с увеличением высоты, то на нижнюю половину гантели Действовала бы большая сила Архимеда, чем на верхнюю, и это противодействовало бы силам Ньютона. Для стальной гантели положение устойчивого равновесия - вертикальное, для пробковой - горизонтальное (на малых высотах над Землей, где атмосфера достаточно плотна).

Разумеется, в условиях атмосферы эти силы из-за своей малости не могут дать о себе знать, так как силы трения о воздух и особенно силы, вызванные перемещениями воздуха, существенно больше. Однако это не значит, что рассмотренные здесь явления не имеют практического значения. Ведь существует среда, в которой нет ни ветра, ни воздуха вообще и в которой гантель может быть "подвешена" без нити. Это космическое пространство. Если на экваториальную орбиту вывести спутник, имеющий форму гантели, то на ближнюю к Земле половину спутника будет действовать большее ускорение свободного падения, чем на дальнюю, отчего спутник должен установиться стержнем по направлению к центру Земли и сохранять такую ориентацию вечно (рис. 33, а-г). Практическое значение такой ориентации состоит в том, что на ближнем к Земле конце гантели можно укрепить фотоаппарат, телевизионную камеру, и они будут все время направлены на Землю, что позволит вести из космоса непрерывный репортаж о нашей планете (например, о состоянии облачности на всем земном шаре). Можно укрепить остронаправленную антенну.

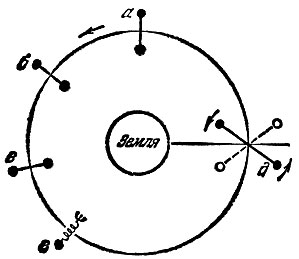
Рис. 33

В космосе стержень гантели может быть очень тонким (струна): на орбите благодаря невесомости стержень будет растягиваться не стержень будет растягиваться не всей силой тяжести гантели, а только разницей в силах тяжести, действующих на обе половинки гантели. Это позволяет удлинить "стержень" вплоть до километров, что увеличивает разницу в силах тяготения на его концах.

Как мы уже видели раньше, гантель, прежде чем занять устойчивое вертикальное положение, совершает вокруг него постепенно затухающие колебания. Спутник-гантель тоже будет колебаться^*) вокруг прямой, соединяющей его с центром Земли (рис. 33, д). Но затухнуть сами собой эти колебания не могут: в космосе нет трения. Как же их потушить? Для этой цели предложено несколько вариантов, Один из них состоит в том, чтобы вместо стержня соединять две половины спутника пружиной (рис. 33, г). Колебания спутника вызовут переменные центробежные силы, которые заставят растягиваться и сжиматься пружину, отчего энергия колебаний постепенно израсходуется на разогрев пружины, и колебания прекратятся. Точно так же будут погашены колебания, вызванные ударами о спутник космических пылинок.

^*) (С периодом, близким по величине к периоду обращения вокруг Земли и почти не зависящим от размеров и формы гантели.)

Заметим, что у Земли давно уже существует спутник-гантель. Это Луна. Она не совсем шарообразна и этим чуть-чуть напоминает гантель: всегда направлена на Землю своей большой осью. Ее вращение и колебания были заторможены трением приливов, вызываемых в лунной коре тяготением Земли. И Луна ориентировалась на Землю своей' большой осью^*). А уж потом мы (в предыдущей задаче) ориентировали радиолуч вдоль этой большой оси с помощью тяготения Луны.

^*) (Впрочем, в последнее время эту ориентацию объясняют эксцентричностью ядра, обнаруженной радиолокационными измерениями движения центра масс Луны.)

Для тех, кто еще не потерял интереса к задаче, предлагаем доказательство того, что центр тяжести гантели, подвешенной на нити на Луне, при колебаниях перемена Луне, при колебаниях перемещается по окружности.

Пока гантель была в горизонтальном положении, веса обеих ее половин, Р₁ и Р₂, были одинаковы, поэтому центр тяжести находился на середине стержня, на расстоянии ^l/₂ от его концов (рис. 34). При отклонении стержня на угол Ф вес нижней части гантели P₁ возрос, вес верхней части Р₂ уменьшился. Центр тяжести М есть точка приложения веса тела Р, который является равнодействующей весов P₁ и Р₂. Точка приложения равнодействующей двух параллельных сил (а они почти параллельны) делит расстояние между точками приложения составляющих на части, обратно пропорциональные этим составляющим:

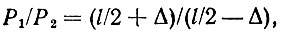
где Δ - расстояние центра тяжести от точки подвеса.

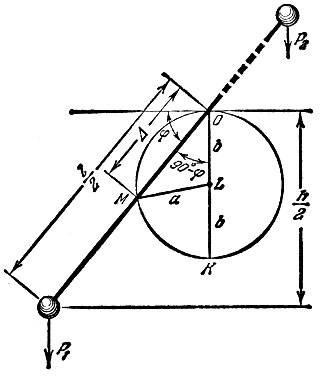
Рис. 34

Концы гантели при отклонении на угол φ разнесены по высоте на величину h, которая и определяет различие весов Р₁ и Р₂, как это было показано раньше:

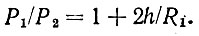
Учитывая, что h = lsin φ, и приравнивая две формулы, имеем

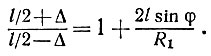
Решаем уравнение относительно Δ. Это дает

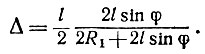
Пренебрегая вторым слагаемым знаменателя (поскольку 2lsinφ << 2R₁), получаем окончательно

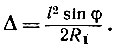
Для тех, кто знаком с полярной системой координат, уже ясно, что это окружность: ведь полусинусоида в полярной системе координат выглядит, как окружность в декартовых. Для остальных же придется продолжить доказательство.

Найдем максимальное значение Δ. Как видно из формулы, Δ = mах, если sinφ = max = 1, т. е. если φ = 90⁰. Подставляя φ = 90°, получаем

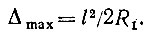
Отложим Δ_mах вертикально вниз от точки О (рис. 34, отрезок ОК) и разделим отрезок ОК точкой L пополам, обозначив две половинки OL и LK буквой b:

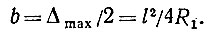
Соединим центр тяжести М и точку L прямой ML = а. Если нам удастся доказать, что при любом значении φ а = b = const, то это будет означать, что точка М при любом значении φ отстоит от точки L на постоянную величину, т. е. перемещается по окружности. Из треугольника MOL по теореме косинусов

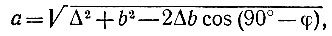
т. е.

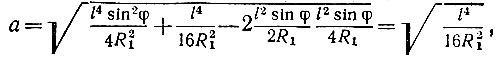
или

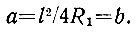
Итак, действительно а не зависит от φ, и, следовательно, кривая, по которой движется центр тяжести М; есть окружность, отрезок а - ее радиус, а точка L - центр.

Разумеется, размеры окружности на рис. 34 сильно преувеличены. Ее диаметр в случае рассмотренной нами лунной гантели равен всего лишь

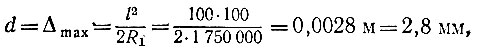
но при увеличении l в 10 раз возрастает в 100 раз.

При очень больших l (десятки и сотни километров) приведенные выше формулы перестают быть правильными, так как силы Р₁ и P₂ становятся заметно непараллельными и, кроме того, в формуле (1) нельзя уже будет пренебречь и третьим слагаемым. Не учитывая этого, мы при l = 5000 км получили бы d ≈ 7000 км > l, что означало бы, что центр тяжести вышел за пределы длины гантели. Это абсурд.