3. Статика

 ●26. Куда направить силу?

Пусть имеются две силы Р и Q (рис. 7), приложенные к одной точке О под углом α друг к другу. Равнодействующая, построенная по правилу параллелограмма сил, найдется из соотношения

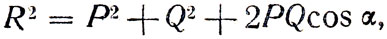
откуда

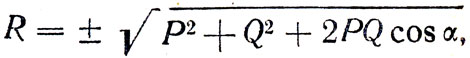
т. е. согласно общепринятому правилу знаков ± (правило Декарта) равнодействующая Rможет быть направлена или внутрь угла α или вне его. Как разрешить это противоречие?

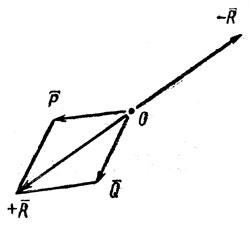
Рис. 7

 ○ 27. Верен ли переместительный закон?

Требуется сложить три силы F₁, F₂, F₃, расположенные в одной плоскости и приложенные к трём точкам тела А, В, С (рис. 8). Сложив для этого силы F₁ и F₂, получим их равнодействующую R₁₂, приложенную в точке D. Перенеся затем силу F₃ вдоль ее линии действия в точку D и сложив здесь с силой R₁₂, найдем равнодействующую R сил F₁, F₂, F₃.

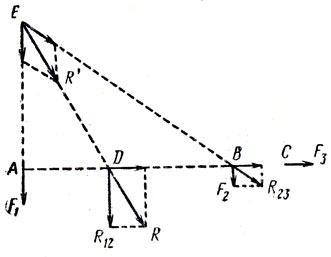
Рис. 8

Однако можно было поступить иначе: сначала сложить силы F₂ и F₃, а затем их равнодействующую R₂₃ сложить с силой F₁. В этом случае получится равнодействующая R', приложенная в точке Е. Нет ли здесь противоречия?

 ●28. Нарушится ли равновесие?

Рычаг АВ уравновешен на оси С силами P₁ и Р₂ (рис. 9). Если приложить силу Q вдоль рычага, то она не должна нарушить его равновесие. Но можно поступить иначе: графически сложить силы Р₁ и Q, получить равнодействующую R, а затем точки приложения ее и силы Р₂ перенести в точку О пересечения их направлений. Равнодействующая S этих сил пересекает точку D рычага. Перенесем в нее точку приложения равнодействующей всех сил рычага S. Теперь необходимо следует вывод: равновесие рычага должно нарушиться. Как разрешить противоречие этого вывода с выводом, сделанным в начале текста задачи?

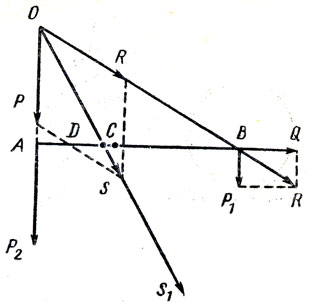
Рис. 9

 ●29. Покатится ли шар?

Тяжелый шар поставили на горизонтальный пол, чтобы он касался стены, наклоненной к полу под тупым углом (рис. 10). Разложим силу тяжести шара Р на составляющие Q и Т. Первая уравновешивается реакцией стены, а вторая, ничем не уравновешиваемая, должна покатить шар вправо. Однако шар остается в покое. В чем ошибка рассуждений?

Рис. 10

 ●30. Прогиб балки.

К доске, лежащей на опорах А и В, приложены силы F₁ и F₂ (рис. 11). Изменится ли стрела прогиба А, если заменить эти силы равнодействующей R?

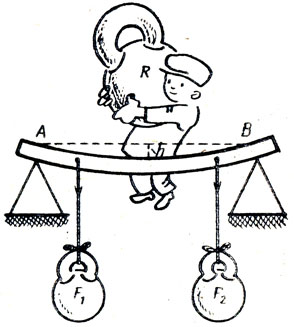
Рис. 11

Решение. По смыслу самого понятия равнодействующая может заменить данную систему сил. Поэтому стрела прогиба не изменится.

С другой стороны, величина момента силы F относительно опоры А (или В) зависит от точки ее приложения. Как разрешить это противоречие?

 ●31. Куда повернется пластинка?

К однородной круглой пластине, лежащей на горизонтальной плоскости, приложены две равные и противоположно направленные силы F₁ и F₂ (рис. 12). В каком направлении станет двигаться точка В?

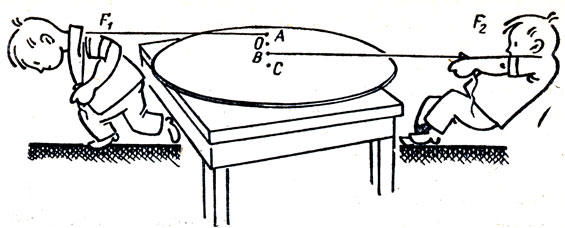
Рис. 12

Решение. Так как силы F₁ и F₂ образуют пару сил, то пластина будет поворачиваться вокруг центра вращения, которым является точка О, находящаяся посередине отрезка АВ. Следовательно, точка В будет двигаться по направлению действия силы F₂.

Но опыт опровергает это решение. Пластинка поворачивается вокруг центра тяжести С, и точка В движется противоположив; направлению силы F₂. Как объяснить этот парадокс?

 ●32. Полет ракеты.

Если на тело не действует внешняя сила, то центр тяжести тела остается неподвижным. Как же обстоит дело с ракетой? Ведь на ракету в космическом пространстве (действием поля тяготения пренебрегаем) внешние силы не действуют, а центр тяжести ракеты, по-видимому, передвигается. Как разрешить противоречие?

 ○33. Какими надо делать концы осей?

Обыкновенно принимается, что величина силы трения не зависит от размеров трущихся поверхностей. Почему же концы осей часовых механизмов и других точных машин делают очень тонкими (рис. 13)?

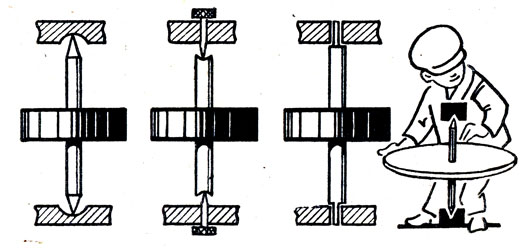
Рис. 13

 ○34. Необычное поведение катушек.

Две катушки с нитками (рис. 14) тянут с одинаковой силой за нить в одном и том же направлении. Однако катушка В приближается к руке и нить наматывается (при этом катушка, вращаясь по ходу часовой стрелки, катится вправо), а катушка А удаляется от руки и нить разматывается (при этом катушка А, вращаясь против хода часовой стрелки, катится влево). Объясните странное поведение катушек.

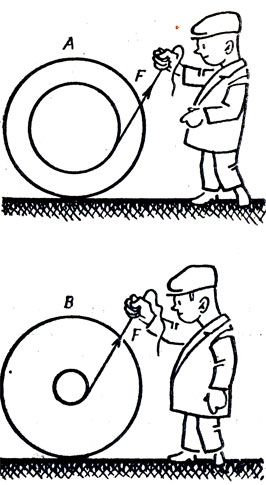
Рис. 14

 ○35. Куда должен двигаться паровоз?

На рисунке 15 изображен паровоз, движущийся влево. В том положении, которое показано на этом рисунке, шатун действует на колесо с некоторой силой, направленной вправо и проходящей выше точки С - точки соприкосновения колеса с рельсом. Но эта точка является мгновенным центром вращения колеса, и под действием этой силы оно должно поворачиваться по часовой стрелке, т. е. катиться вправо. Почему же паровоз движется влево?

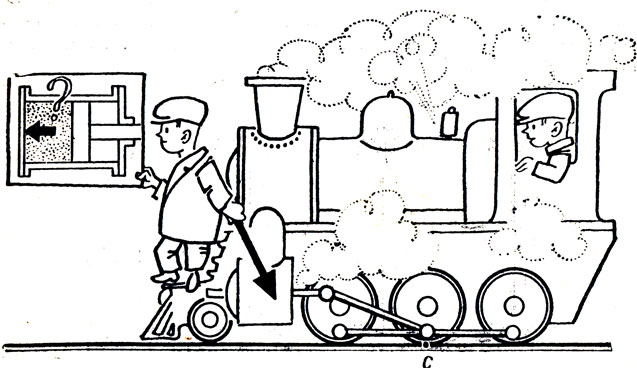
Рис. 15

 ●36. Какие колеса сильнее давят?

На наклонной плоскости стоит равномерно нагруженный вагон, который удерживается в покое силами трения. Какие колеса сильнее давят на рельсы.

Решение. Задачу можно решать двумя способами, которые, казалось бы, приводят к разным ответам. Можно разложить силу тяжести вагона на две параллельные P₁ и Р₂ (рис. 16), проходящие через линии соприкосновения одной и другой пар колес с рельсами. Сразу видно, что сила Р₂ больше.

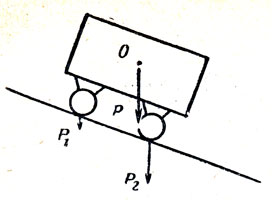
Рис. 16

Но можно поступить иначе - разложить вес вагона Р на две составляющие - параллельную F и перпендикулярную к наклонной плоскости Q (рис. 17). Первая уравновешивается противоположно направленной силой трения, а вторая разлагается на две равные силы нормального давления колес Р₃ и Р₄. Объясните противоречие.

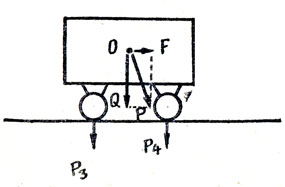
Рис. 17

 ○37. Почему падает мальчик?

Металлический шарик переходит с песчаной дорожки на ледяную. В момент перехода скорость движения шарика не изменяется.

Мальчик бежит по земле, а потом ступает на лед, не меняя скорости. Часто случается, что ноги при этом скользят вперед и мальчик падает.

Получается так, что уменьшение коэффициента трения при переходе на лед увеличивает скорость движения ног (ноги уходят из-под вертикали, проходящей через центр тяжести, мальчик теряет равновесие и падает). Но увеличивать скорость может лишь какая-то сила. А сила трения при переходе мальчика на лед, наоборот, уменьшается. Как разрешить парадокс?

 ●38. Вечный двигатель Чепера.

На рисунке 18 изображен один из типичных проектов вечного двигателя с откидывающимися грузами. На валу укреплено зубчатое колесо с характерной формой зубьев. К ободу колеса в нижней части зубьев шарнирно крепятся стержни с грузами на концах. Движение стержней ограничено одной или другой стороной двух соседних зубьев. По мысли изобретателя Чепера, откинутые направо грузы, имея большее плечо, создадут больший вращательный момент и приведут колесо во вращение по направлению движения часовой стрелки. В чем ошибка проекта?

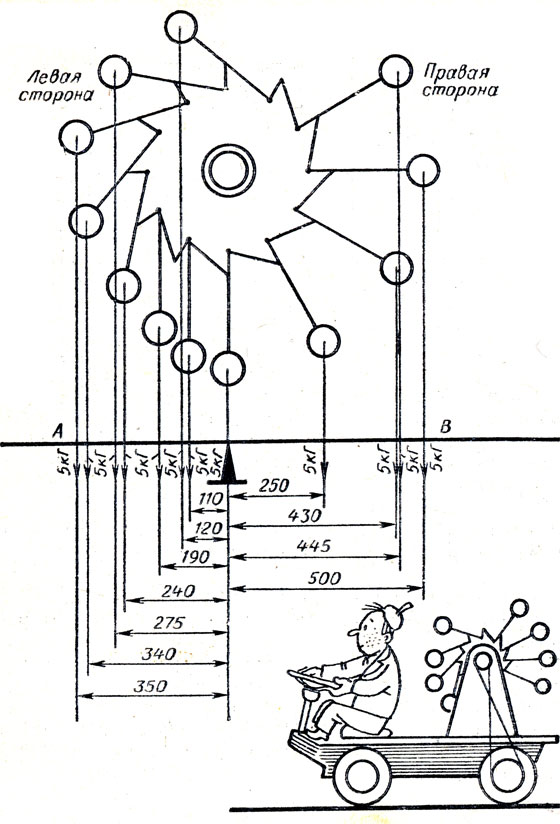
Рис. 18

 ●39. Вечный двигатель В. д' Оннекура.

В 1245 г, архитектор Виллар д'Оннекур разработал чертеж, а затем изготовил модель колесного вечного двигателя. На ось надето свободно вращающееся колесо (рис. 19). К его ободу прикреплены на шарнирах семь стержней, имеющих на концах грузы. Справа стержни с грузами прилегают к ободу колеса, а слева откидываются и являются продолжением спиц колеса. Таким образом грузы слева находятся значительно дальше от оси вращения колеса, чем грузы справа. На основании этого В. д'Оннекур считал, что равновесие колеса будет постоянно нарушенным и оно должно вращаться вечно, не требуя постороннего подталкивания. Вращение колеса против часовой стрелки будет поддерживаться непрерывными толчками откидывающихся грузов. Но... это предложение изобретателя оказалось неверным. Колесо, совершив несколько оборотов, останавливалось. Колесо вращалось до тех пор, пока не иссякла энергия, сообщенная ему в момент пуска механизма. В чем ошибка проекта?

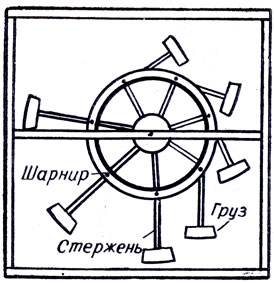
Рис. 19

 ●40. Вечный двигатель Э. Сомерсета.

Англичанин маркиз Эдвард Сомерсет построил механизм, который должен был "вечно" двигаться. Это было колесо диаметром 14 футов (4,27 м), а приводилось оно в движение 14 грузами, по 22 кг каждый (на рис. 20 изображено 12 грузов). Но, несмотря на то что этот "вечный двигатель" построил маркиз, успех все же не был обеспечен. Он также бездействовал, как и все предыдущие. В чем ошибка проекта?

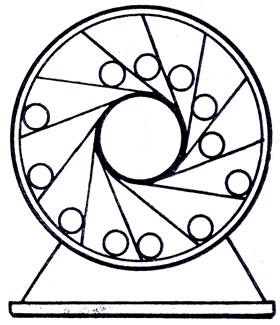
Рис. 20

 ○41. Конус, катящийся вверх.

Известен прибор для иллюстрации явления механического парадокса. Прибор состоит из двойного деревянного конуса и двух деревянных пластинок в форме прямоугольных трапеций, сходящихся под углом α (рис. 21). Для каждого прибора существует свой угол α_крит, зависящий от геометрических элементов пластин и конуса. Если раздвинуть пластины на угол, больший α_крит, то двойной конус катится вверх от вершины двугранного угла. Объясните этот парадокс.

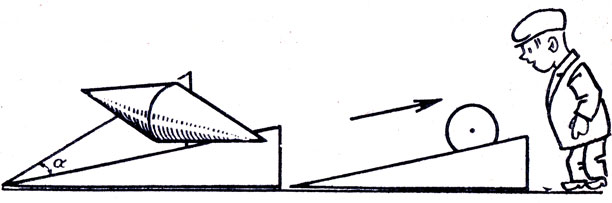
Рис. 21

 ○42. Чудо не есть чудо.

На титульной странице трактата по статике известного голландского физика С. Стевина в лейденском издании 1586 г. имеется рисунок с надписью на фламандском языке: "Чудо не есть чудо". Эту надпись можно расшифровать следующим образом: смотри на этот рисунок, и ты обнаружишь здесь на первый взгляд чудо, а потом, после размышления, ты найдешь закон природы - не чудо.

На рисунке 22 представлена треугольная призма с горизонтальной нижней стороной и двумя другими, из которых одна вдвое длиннее другой. На призме равномерно распределены 14 тяжелых, равных по весу шаров. Так как нижнюю симметричную часть цепи можно не принимать во внимание, то отсюда следует, что четыре шара уравновешиваются двумя шарами. Как объяснить это "чудо"?

Рис. 22

"Не будь этого,- пишет Стевин,- ряд шаров должен был бы (придя в движение) занимать то же положение, что и раньше. По той же причине восемь шаров левых должны были бы быть более тяжелы, чем шесть правых, и, следовательно, эти восемь должны были бы опускаться вниз, а шесть - подниматься вверх, так что шары совершали бы непрерывное и вечное движение". Но вечное движение данного устройства Стевин считал невозможным. Как же объяснить парадокс?

 ●43. Вечный двигатель К. Кайля.

Минный машинист из Прибалтики К. Кайль предложил следующий проект вечного двигателя. Свободно вращающееся на валу зубчатое колесо А (рис. 23) охвачено цепью, натянутой на трех роликах, расположенных в вершинах равностороннего треугольника. На цепи закреплены три равных груза 1, 2, 3, которые (по мысли автора) должны являться причиной вечного движения. Кайль предполагал, что грузы 1 и 2, стремясь передвинуться по направлению, указанному на рисунке стрелками, безусловно поднимут груз 3. Вследствие того что цепь представляет собой равносторонний треугольник, грузы 1 и 2 постоянно будут стремиться вниз, а груз 3 подниматься вверх.

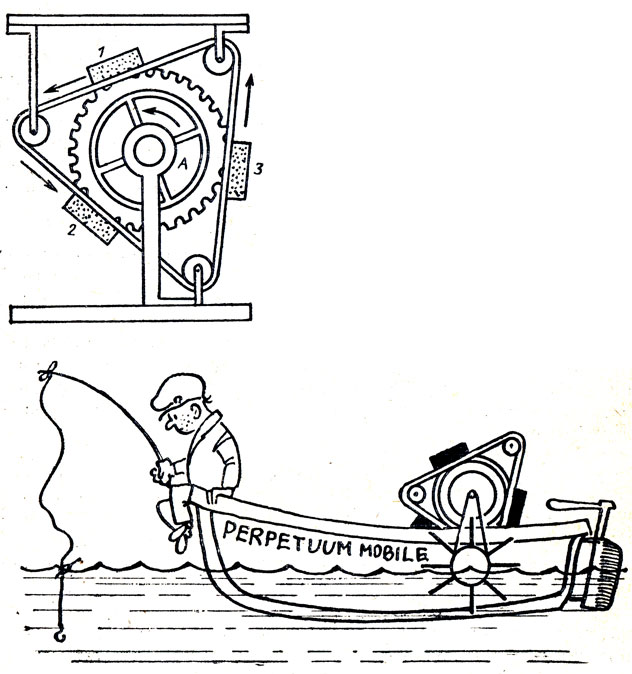
Рис. 23

Несмотря на кажущуюся убедительность доводов автора, это устройство не работало. В чем ошибка проекта?

 ●44. Еще один проект вечного двигателя.

Сравнительно недавно (в 1915 г.) был создан оригинальный колесный вечный двигатель с перекатывающимися шариками. Изготовленная автором модель состояла из колеса около метра в диаметре и шести шариков (рис. 24). На колесе имелся спиральный канал, в котором всегда находилось 5 шариков. Шестой, провалившись в отверстие, имеющееся у края колеса, перекатывался по специальному изогнутому ходу под спиральным каналом к отверстию у центра. Отсюда он попадал в начало-"центр" спирального канала, а в это время другой шарик попадал в изогнутый канал. Сила тяжести шариков приложена к колесу несколько левее оси вращения колеса. Поэтому, перекатываясь по спирали, как по наклонной плоскости, они должны, по мысли изобретателя, являться причиной вращения колеса. Почему изобретателя постигла неудача?

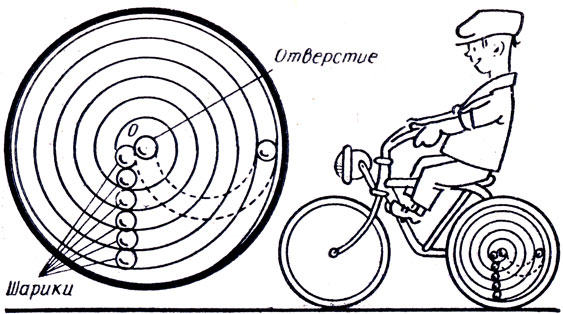
Рис. 24

 ●45. А цилиндры все-таки раскатываются!

Три одинаковых цилиндра расположены на горизонтальной площадке так, как изображено на рисунке 25. Сила тяжести Р нижних двух проходит через центры вращения каждого, поэтому она не может вызвать вращения цилиндров. Вес верхнего цилиндра Р разложим на направления О₁О и О₂О. Эти составляющие проходят через оси нижних цилиндров, поэтому они также не вызовут их вращений. Следовательно, даже при полном отсутствии трения цилиндры не должны раскатиться. Что, конечно, опровергается опытом. В чем софистика рассуждений?

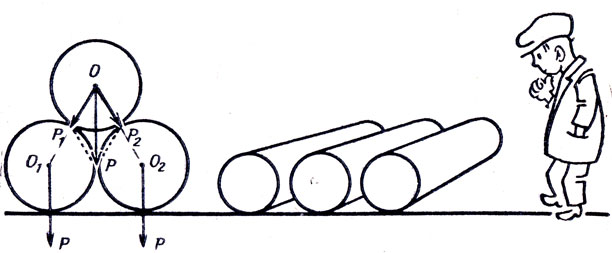
Рис. 25

 ○46. Сохранит ли равновесие велосипедист?

Корабль идет с постоянной скоростью v. По палубе от носа к корме движется велосипедист с такой же скоростью относительно корабля. Следовательно, относительно берега велосипедист остается неподвижным. В таком случае, как всякий неподвижный велосипедист на земле, он не сможет сохранить равновесие.

Но опыт опровергает этот вывод. Велосипедист и на испытательном стенде движется относительно "своей дороги", оставаясь неподвижным относительно земли, и сохраняет равновесие. Как объяснить "парадокс велосипедиста"?