4. Гидро- и Аэростатика

 ○47. Дальность полета

Тело, брошенное горизонтально, имеет тем большую дальность полета, чем большей высоты оно брошено (при прочих равных условиях). В известном опыте по давлению жидкости стенки сосуда (рис. 26) длительность полета водяных струй не увеличивается с высотой, а уменьшается. Объясните это кажущееся противоречие.

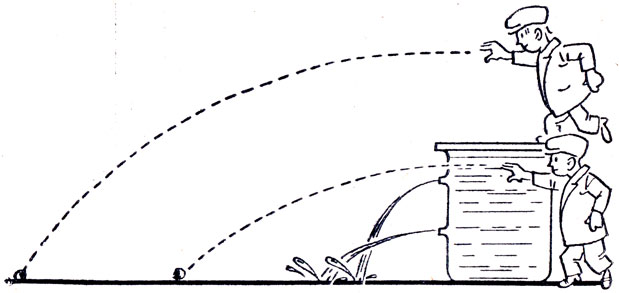
Рис. 26

 ○48. Опыт Паскаля.

Разрыв бочки в опыте Паскаля (рис. 27) представляет парадокс, так как единственная действующая здесь сила - тяжесть воды в трубке для этого, очевидно, недостаточна; для разрыва бочки обуется сила, значительно боляьша, чем вес бочки вместе с водой. Откуда же берется эта дополнительная огромная сила?

Рис. 27

 ●49. Еще раз об опыте Паскаля

В известном опыте Паскаля (см. задачу № 48) давление в бочке с водой создается весом столба воды в трубке. Если удвоить силу, действующую на тело, то удвоится и давление. Следовательно, если вместо одной трубки с водой взять две (рис. 28), то давление воды на стенки бочки должно увеличиться вдвое.

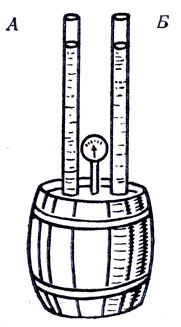
Рис. 28

Соберем установку, изображенную на рисунке 28. Манометр, показывающий давление, производимое на жидкость, при замене одной трубки двумя не изменяет своих показаний. В чем ошибка рассуждений?

 ○50. Парадокс Паскаля.

Сосуд EADCBF с приставным дном CD опущен в резервуар с водой (рис. 29). Вода в объеме ABCD имеет массу 2,5 кг, значит, она весит 24,5 н. Если на дно CD поставить узкий цилиндр весом 25 н, то оно не отрывается, а если налить 2,5 кг воды, то оно отрывается. Объясните парадокс.

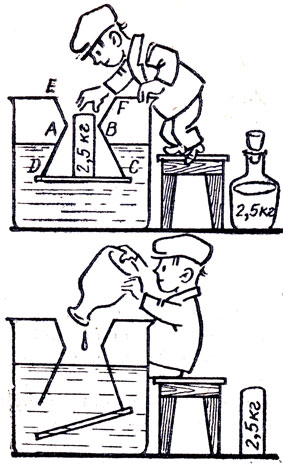
Рис. 29

 ○51. Еще один парадокс Паскаля.

Закон Паскаля формулируется так: если на какую-либо часть поверхности жидкости, заключенной в закрытый со всех сторон сосуд, производится давление, то оно передается через жидкость во все стороны одинаково. В соответствии с этим давления на площадки А и В (рис. 30), находящиеся в верхнем и нижнем частях сосуда, должны быть одинаковы. Ибо если бы на одну из них давление было больше, чем на другую, то согласно закону Паскаля избыток давления целиком передался бы другой площадке и в итоге давления оказались бы равными.

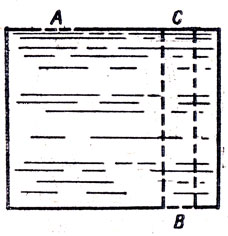
Рис. 30

Но, с другой стороны, известно, что давление в какой-либо точке тяжелой и спокойной жидкости равно весу столба жидкости, высота которого ВС равна глубине погружения точки, а основание-единице. Следовательно, на площадку В жидкость будет производить давление, а на площадку А - не будет. Как разрешить эти два противоречащих друг другу вывода?

 ●52. Вечный гидростатический двигатель.

В цилиндре, заполненном жидкостью, имеется поршень, форма которого изображена на рисунке 31. Слева на поршень действует некоторая сила. Так как справа площадь поршня больше, чем слева, то можно ожидать большую силу давления на воду. А раз так, то можно как будто получить и большую работу при некотором перемещении поршня влево, В чем ошибка таких рассуждений?

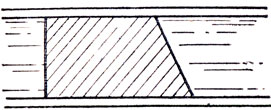
Рис. 31

 ●53. Закон сообщающихся сосудов.

В одинаковых сообщающихся сосудах А и В находится комнатная вода (рис. 32). Кран К закрыли и воду в сосуде В нагрели, вследствие чего ее уровень немного повысился. Станет ли вода переливаться из одного сосуда в другой, если открыть кран?

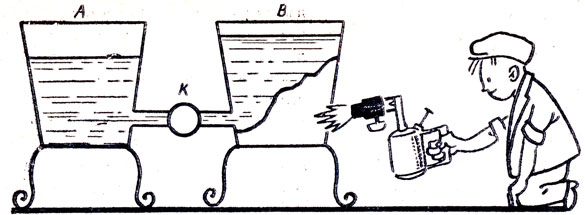
Рис. 32

Решение. Один ученик сказал, что увеличение высоты столба жидкости в сосуде В вызовет увеличение давления на уровне соединительной трубки. Поэтому жидкость будет перетекать из сосуда В в сосуд А, если открыть кран К

Другой ученик утверждал, что после нагревания воды в сосуде В давление в обоих сосудах не изменилось, так как не изменились вес воды и площадь основания дна сосуда.

Третий ученик доказывал, что давление воды в сосуде В на уровне соединительной трубки после ее нагревания уменьшится. И если открыть кран К, то вода будет перетекать из сосуда А в сосуд В. Это происходит потому, что сосуд В расширяется кверху, и увеличение высоты уровня воды в нем не будет обратно пропорционально уменьшению плотности, вызванному нагреванием воды. Кто же из учеников прав?

 ●54. Вечный гидродинамический двигатель.

Большая круглая железная труба, изогнутая в виде кольца с просветом между точками А и В (рис. 33), наполовину закапывается в землю и наполовину висит над землей. Мельничное колесо, состоящее из ряда лопаток, насаженных на ось, помещается внутри подземной части трубы в точке В. Если в эту трубу, в левую ее половину, возле точки В сразу вылить 2-3 бочки воды, то (по мнению автора проекта) эта вода с разгона помчится по трубе, дойдет до точки А, снова обрушится вниз и т. д., попутно приводя мельничное колесо в быстрое вращательное движение. Единственное, что якобы необходимо для дальнейшей бесперебойной работы мельницы,- это время от времени подливать в трубу воду для замены той, которая испарилась. В чем ошибка проекта? Как фактически стала бы двигаться вода в трубе?

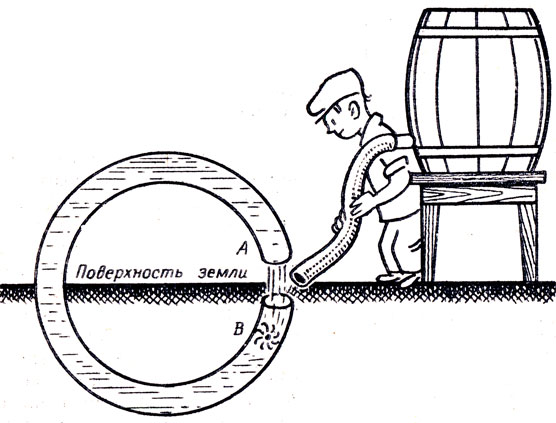
Рис. 33

 ○55. Что удерживает воду в стакане?

Полный стакан с водой, взятой при температуре 20°С, накрывают листом бумаги и, придерживая лист, переворачивают стакан. Затем убирают руку, которая придерживала лист. Вода не выливается. Ее удерживает атмосферное давление.

Повторим тот же опыт без листа бумаги. Вода выливается из стакана. Но ведь атмосферное давление существовало и в этом случае, а результат получился другой. Как объяснить этот парадокс?

 ○56. Сколько весит барометрическая трубка?

К чашке равноплечих весов подвешена тонкостенная цилиндрическая барометрическая трубка со ртутью (рис. 34). Конец трубки лишь на ничтожную глубину погружен в чашку со ртутью. Чтобы уравновесить весы, надо на другую чашку весов поместить груз, вес которого равен сумме весов трубки и ртутного столба в ней.

Но ведь ртуть в трубке (если пренебречь трением ртути о стенки) своим весом давит на ртуть в чашке, а не на трубку, Как разрешить это противоречие?

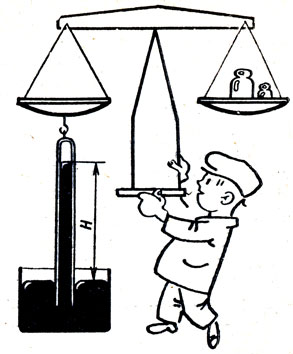
Рис. 34

 ●57. "Вечный" насос.

Был предложен следующий проект "вечного" насоса. На берегу реки ставится железный бак с краном А и трубой В (шлангом), опущенным в реку (рис. 35). Для того чтобы привести устройство в действие, надо через кран А выкачать из бака воздух и наполнить его водой. Если затем отключить воздушный насос и открыть кран А, то вода (по мнению изобретателя) в силу своей тяжести потечет из крана, а атмосферное давление по трубке В будет поставлять в бак все новые и новые количества воды. В чем ошибка проекта?

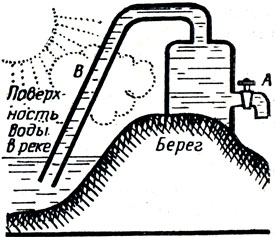
Рис. 35

 ●58. Еще один проект "вечного" насоса.

Сосуд, имеющий форму, изображенную на рисунке 36, заполнен водой. Радиус отверстия А равен радиусу трубки В. Что произойдет, если вынуть пробку А? Явлениями капиллярности пренебречь.

Рис. 36

Решение. Под действием веса жидкость будет вытекать из отверстия А. Одновременно в расширенную часть С будут поступать через трубку В новые количества жидкости.

Опыт опровергает это решение. В чем ошибка рассуждений?

 ○59. Почему не текла вода по трубе?

Резиновый шланг, внутренний диаметр которого 15-20 мм, намотан на барабан диаметром 300 мм (рис. 37). Один конец шланга опущен в ведро, а другой поднят над барабаном примерно на 1 м. В шланге воды нет. На нем нет ни кранов, ни зажимов. Если вставить воронку в верхний конец шланга и начать наливать в нее воду из водопровода, то вода из нижнего конца шланга не польется. А ведь давление воздуха у верхнего и нижнего концов шланга одинаковое. Как объяснить этот парадокс?

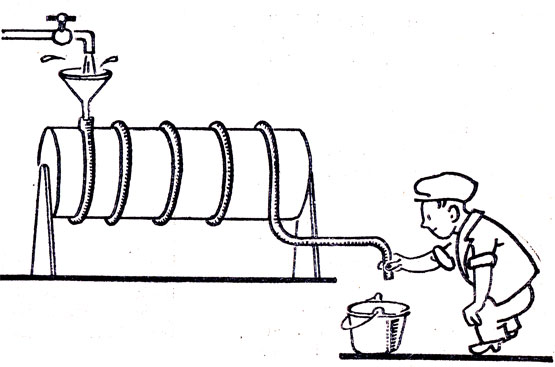
Рис. 37

 ●60. Одинаковы ли показания барометра в закрытом и открытом помещениях?

Один из учеников утверждал, что на открытом воздухе барометр покажет большее давление, чем в помещении. Другой считал, что показания барометра будут одинаковы. Когда они заметили показания барометра в физическом кабинете на четвертом этаже и во дворе школы, то давление во дворе оказалось больше, чем в кабинете. Значит ли это, что первый ученик был прав?

 ●61. Фонтан Герона.

Физик древности Герои Александрийский предложил оригинальную конструкцию фонтана (рис. 38). Вначале сосуд Л наполняют водой и некоторое количество воды наливают в сосуд С. Получится ли вечный круговорот воды в системе: сосуд С, трубка 1, сосуд В, трубка 2, сосуд А, трубка 3, струя 4, сосуд Сит. д.? Так как фонтан является действующей системой (в чем легко убедиться на опыте, соорудив его из консервных банок), то не нарушается ли закон сохранения энергии: вода в струе 4 поднята на более высокий уровень, чем она была в сосуде С?

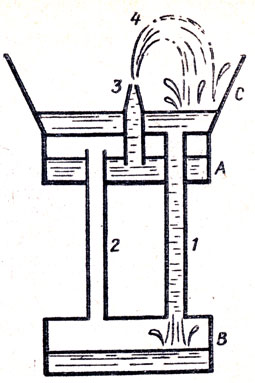
Рис. 38

 ○62. Почему не сжимается резина?

При открытом кране (рис. 39) через трубку В накачивают резиновый шар С. Он раздувается, и резина растягивается. Закрывают кран и отсоединяют насос. Однако воздух из трубки В не выходит, хотя его и должна выталкивать, сжимаясь, упругая резиновая оболочка шара. Объясните парадокс.

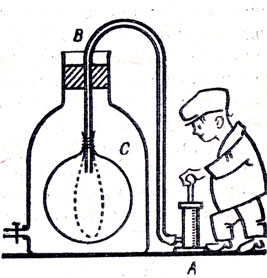
Рис. 39

 ●63. Давление воды на дно сосуда.

В сосуде с водой плавает стакан, в котором находится камень. Как изменится уровень воды в сосуде, если из стакана вынуть камень и опустить его в сосуд?

Решение. При перенесении камня в сосуд общий вес воды, камня и стакана не меняется. Площадь дна сосуда тоже не меняется. Следовательно, давление системы трех тел на дно сосуда не должно измениться. Но давление столба воды на дно сосуда з=ρпр, где ρ - плотность воды, g - ускорение силы тяжести, h - высота столба. Следовательно, уровень воды в сосуде не должен измениться.

Проделаем соответствующий опыт и убедимся, что уровень воды в сосуде понизится. В чем ошибочность решения?

 ●64. Как рассчитать выталкивающую силу?

В сосуде со ртутью плавает чугунный цилиндр с достаточно широким основанием, а сверху налита вода (рис. 40). Определить выталкивающую силу, действующую на цилиндр.

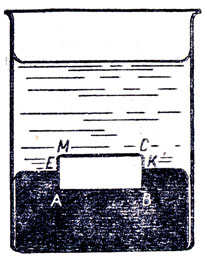
Рис. 40

Решение. На нижнюю часть цилиндра действует выталкивающая сила, равная весу ртути в объеме АВКЕ. На верхнюю часть действует выталкивающая сила, равная весу воды в объеме ЕКСМ. Следовательно, сила, которая выталкивает цилиндр, равна весу ртути в объеме АВКЕ плюс вес воды в объеме ЕКСМ.

С другой стороны, вода оказывает на ртуть некоторое давление, которое передается на нижнее основание цилиндра АВЛ Следовательно, выталкивающая сила, действующая на нижнюю часть цилиндра АВ, больше веса ртути в объеме АВКЕ. Наряду с этим сила, с которой вода действует на верхнюю часть цилиндра, будет не выталкивающей, а погружающей. Следовательно, сила, которая выталкивает цилиндр, равна разности сил давления на верхнее и нижнее его основания. Однако расчет показывает, что выталкивающая сила равна весу ртути в объеме АВКЕ плюс вес воды в объеме ЕКСМ. Какое же из решений является научно более строгим?

 ○65. Положение центра тяжести плавающего бруска.

В сосуде со ртутью плавает чугунный брусок. Изменится ли положение центра тяжести бруска по отношению к уровню ртути, если в сосуд налить воды (см. задачу № 64)?

Решение. Вода давит на брусок сверху и с боков. Силы давления на брусок с боков уравновешиваются, а сила давлений на брусок сверху должна понизить положение центра тяжести бруска по отношению к уровню ртути.

Проделаем соответствующий опыт и обнаружим, что брусок в ртути не опускается, а немного всплывает. В чем ошибочность представленного выше решения?

 ○66. Когда тело находится в устойчивом равновесии?

Известно положение о том, что равновесие тела тем более устойчиво, чем ниже расположен его центр тяжести. На рисунке 41 показаны два положения плавающей льдины. Положение б несомненно является более устойчивым, но центр тяжести льдины находится выше, чем в положении а. Как разрешить это противоречие?

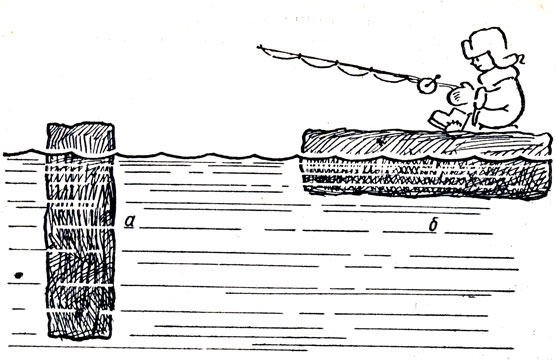
Рис. 41

 ○67. Как совершился переход энергии?

Кусок дерева, помещенный на дно сосуда с водой, всплывая, приобрел кинетическую энергию. Согласно закону сохранения, энергия не может возникнуть "из ничего". Какое же тело передала энергию куску дерева?

 ○68. Нарушается ли закон сохранения энергии?

Обычно считают, что сифоном можно переливать жидкость из верхнего сосуда в нижний. Если в большой сосуд с водой поместить два сосуда А и В, причем в первом находится керосин, а во втором - вода (рис. 42), и соединить их трубкой, то керосин будет переливаться из нижнего сосуда А в верхний сосуд В.

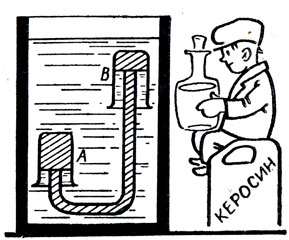
Рис. 42

Таким образом, керосин, всплывая, увеличивает свою потенциальную энергию по отношению к Земле. Не противоречит ли этот опыт закону сохранения энергии?

 ○69. Земные и лунные ареометры.

Двое учащихся поспорили. Один сказал, что космонавтам придется изменить шкалу (увеличить деления в 6 раз) земного ареометра, когда им придется пользоваться на Луне, так как сила тяжести на ней в 6 раз меньше, чем на Земле.

Другой доказывал, что земными ареометрами можно пользоваться на любой планете, ибо если в некоторое число раз изменяется вес самого ареометра, то во столько же раз изменяется и вес вытесненной им воды. Кто же из них прав?

 ●70. Почему опрокинулась кювета?

Кювета с водой стоит на бруске (рис. 43). На воде плавает коробочка с гирей. Кювета находится в равновесии.

Рис. 43., Рис. 44

Если вынуть гирю из коробочки и поставить на дно кюветы под тем местом, где плавала коробочка, то равновесие нарушится (рис. 44), хотя вес левой части кюветы как будто бы не изменился. Объясните ошибку рассуждений.

 ●71. Какой необходим груз?

Если в установке, изображенной на рисунке 45, пережечь нить АВ, то тело Р, имеющее объем 100 см³, целиком погружается в воду и остается висеть на нити АСВ. При этом равновесие весов нарушается. На какую чашку весов и какой добавочный груз необходимо положить, чтобы восстановить равновесие?

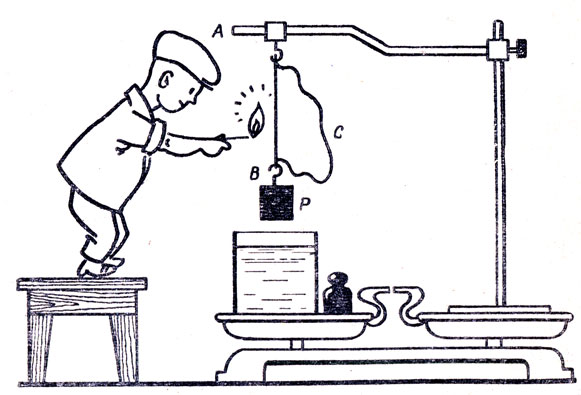
Рис. 45

Решение. В соответствии с законом Архимеда тело Р, погруженное в воду, будет выталкиваться вверх с силой 0,98 н. Поэтому на правую чашку весор будет действовать вес штатива и вес тела Р, уменьшенный на вес вытесненной им воды.

Следовательно, для восстановления равновесия весов необходимо щ правую чашку поставить гирю массой 100 г.

Однако опыт показывает, что на правую чашку весов необходимо поставить гирю массой 200 г. В чем ошибка решения?

 ●72. Какая часть сосуда тяжелее?

Симметричный относительно вертикальной плоскости ОК сосуд ABCD (рис. 46) наполнен водой и опирается о ребро неподвижной призмы. В правую часть сосуда опустили кусок алюминия массой 0,5 кг, а в левую - кусок свинца массой 0,4 кг. Какая часть сосуда перетянет?

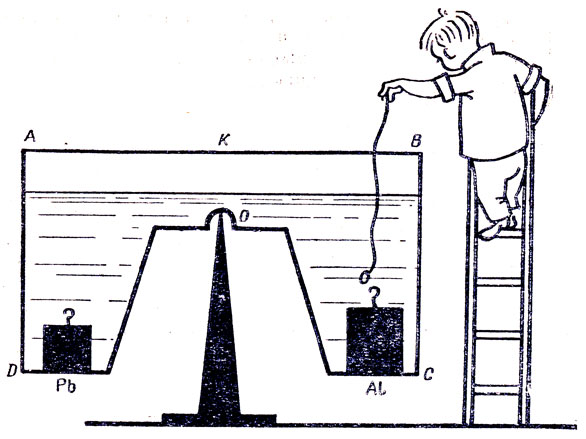
Рис. 46

Решение. Сосуд представляет собой сложный равноплечий рычаг. Так как вес куска алюминия больше, чем свинца, то перетянет правая сторона сосуда, где лежит кусок алюминия.

Опыт, однако, опровергает это заключение. В чем ошибка решения?

 ○73. Капризный поплавок.

В высокий стеклянный цилиндрический сосуд помещают песочные часы, наливают воды до самого верха и закрывают крышкой (рис. 47). Часы всплывают под самую крышку. Затем цилиндр переворачивают. Часы не всплывают (рис. 48), хотя они окружены водой и выталкивающая сила больше веса часов. Через определенный промежуток времени, когда некоторое количество песка высыплется в нижнее отделение, часы начнут медленно всплывать. Таким образом, перетекание песка из верхнего отделения часов в нижнее влияет на его плавучесть. Но ведь часы герметически закрыты и вес их от перетекания песка не изменяется. Как объяснить этот парадокс?

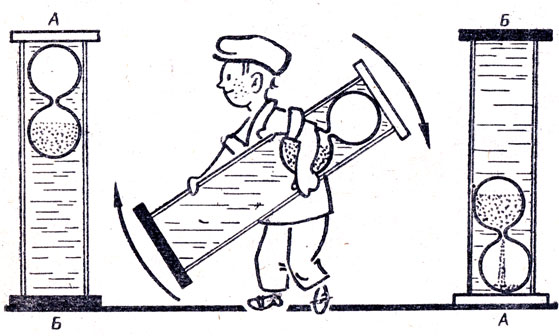
Рис. 47., Рис. 48

 ●74. Как избежать перегрузки?

Взлет космического корабля с Земли происходит с ускорением, в несколько раз превышающим ускорение силы тяжести. Поэтому находящийся в корабле космонавт подвергается действию перегрузки (силы, прижимающей человека к опоре).

Чтобы избежать перегрузки, предлагают помещать космонавта в камеру с водой (плотность воды примерно равна плотности человеческого тела). Авторы проекта считали, что человек, находясь в воде, становится невесомым и, следовательно, совершенно избавляется от действия как естественной, так и искусственной тяжести (перегрузки). В чем состоит ошибка такого заключения?

 ●75. Простой проект вечного двигателя.

Рассмотрим один из проектов вечного двигателя. В вырез стенки АВ бака с жидкостью вставлен вал (рис. 49), ось которого О лежит в плоскости стенки АВ.

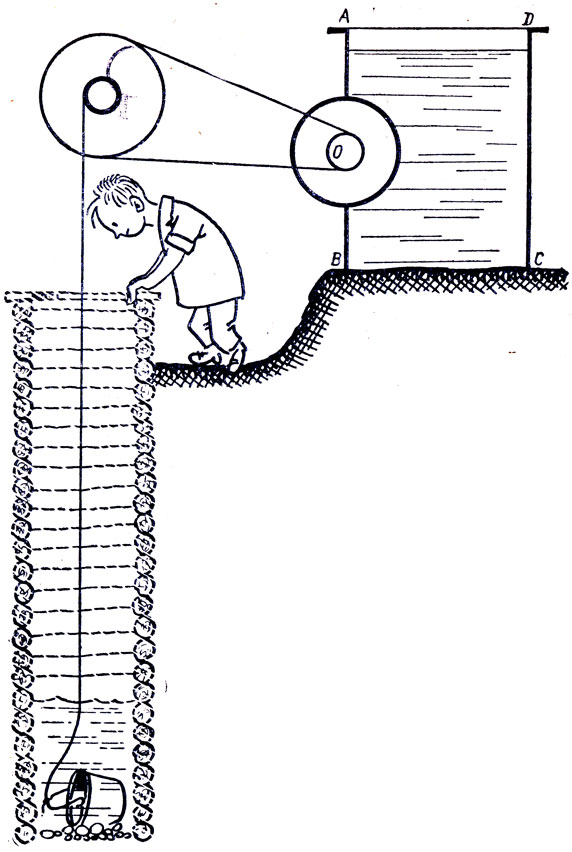
Рис. 49

Вал закрывает собой весь вырез, так что жидкость не выливается; вал может вращаться на своей оси. На половину вала, погруженную в жидкость, по закону Архимеда действует подъемная сила, которая, по мысли изобретателя, должна вызвать вращение вала против часовой стрелки. Это вращение должно было бы продолжаться вечно. В чем ошибка проекта?

 ●76. Вечный двигатель Леонарда.

Швейцарец Г. Леонард в 1865 г. предложил следующий проект вечного двигателя. Бесконечная цепь из жестяных поплавков проходит правой половиной сквозь сосуд В с водой (рис. 50). По мысли автора, поплавки, стремясь всплыть, будут вращать колесо С, через которое эта цепь переброшена, против движения часовой стрелки. В чем ошибка проекта?

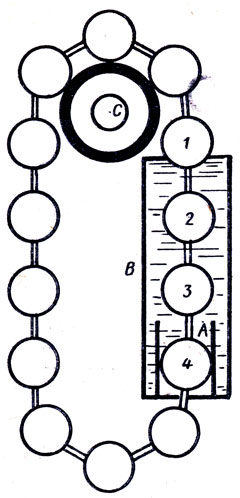
Рис. 50

 ●77. Вечный двигатель времен Леонардо да Винчи.

В XV в. был предложен проект вечного двигателя, основанный на законе Архимеда¹. В проекте этого вечного двигателя имеется колесо с семью откидывающимися на шарнирах грузами (рис. 51). Изобретатель погрузил х одну треть колеса в воду, обоснованно предполагая, что вес этой части колеса и грузов уменьшится по известному закону Архимеда и колесо придет во вращение. В чем ошибка проекта?

¹ (Чертеж проекта был обнаружен в записях и набросках знаменитого итальянского художника и ученого Леонардо да Винчи. Достоверно известно, что он не занимался изобретательством вечного двигателя. По-видимому, этот чертеж попал к нему на заключение от какого-либо итальянского изобретателя.)

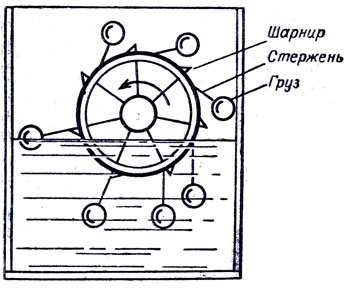
Рис. 51

 ●78. Вечный двигатель В. Конгрева.

Английский артиллерист и инженер Вильям Конгрев сконструировал вечный двигатель, состоящий из трехгранной призмы с роликами К, М, Н на углах и губками, натянутыми вокруг призмы (рис. 52). Все это частично погружено в воду. Изобретатель полагал, что вес губки А увеличится за счет впитавшейся воды. Вследствие этого нарушится равновесие и лента с губками передвинется. Затем впитает воду губка В, ставшая на место губки А, лента снова повернется, и так бесконечно. Чтобы увеличить разницу между весом губок, вышедшей из воды над роликом К и погружающейся в воду у ролика М (т. е. более надежно обеспечить движение), автор предусмотрел выжимание воды из губок над роликом К посредством грузов Р, прикрепленных к губкам. Но... двигатель не работал. В чем ошибка проекта?

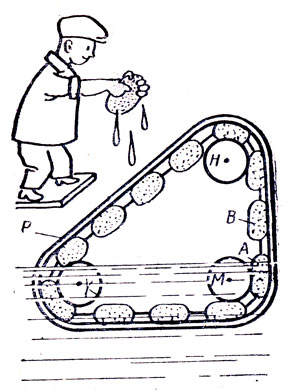
Рис. 52

 ●79. Сила сопротивления воздуха.

Шар движется в воздухе, имея в данной момент скорость v (рис. 53). Так как сила сопротивления воздуха пропорциональна квадрату скорости, то ее можно представить в виде F=kv², где k - коэффициент пропорциональности.

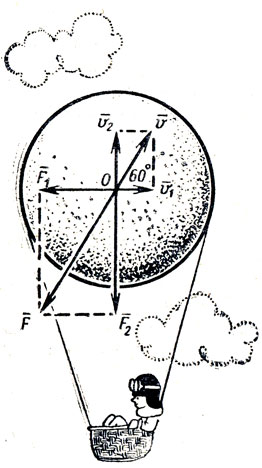
Рис. 53

С другой стороны, разложив скорость v на горизонтальную и вертикальную составляющие, получим: v₁ = vcos60° и v₂ = vsin60°. Следовательно, F₁ = kv₁² =kv²cos²60° и F₂ = kv₂² = kv²sin²6O°, где F₁ и F₂ - силы сопротивления, вызванные составляющими v₁ и v₂. Таким образом, полная сила сопротивления равна:

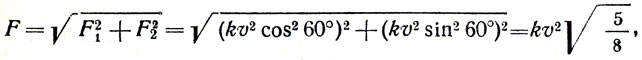
что не совпадает с выражением F = kv². Как разрешить это противоречие?

 ○80. Падают ли облака?

Все тела падают на землю. Облака состоят из мелких капелек воды, Значит, облака должны падать на землю.

Однако никому не удавалось наблюдать, чтобы облако, опускаясь, когда-нибудь достигло земли. Как разрешить этот парадокс?

 ○81. Как надо стрелять из летящего самолета.

При испытании реактивного снаряда, установленного в хвосте самолета для его защиты от нападения сзади, был обнаружен удивительный парадокс. При выпуске снаряда он сначала удалялся от самолета, а затем разворачивался и догонял самолет. Как можно объяснить это явление?

24xxx.me/tags/armyanki/