5. Работа и энергия

 ○82. Как совершить работу в 1 дж?

Груз весом 1 н поднимают на высоту 1 м. При этом может быть совершена работа, равная 1 дж или большая, чем 1 дж. Когда это возможно? Нет ли здесь противоречия?

 ●83. Как совершить работу меньше 1 дж?

Будет ли совершена работа меньше 1 дж, если камень весом 1 н поднимать на высоту 1 м в воде?

Решение. Так как на камень в воде действует выталкивающая сила, то для его поднимания надо прилагать силу, меньшую, чем 1 н. Следовательно, и работа будет совершена меньшая, чем 1 дж. Но представим себе, что каким-то образом удалена вода после того, как камень поднят. Тогда камень весом 1 н, поднятый на высоту 1 м, обладал бы потенциальной энергией в 1 дж. Выходит, что либо затраченная на поднятие камня энергия меньше, чем полученная (что противоречит закону сохранения энергии), либо при его подъеме все-таки совершена работа в 1 дж (но это противоречит вышеприведенному решению). Как разрешить эти противоречия?

 ○84. Всегда ли работа равна нулю, если сила перпендикулярна перемещению?

Неподвижный блок изменяет направление движения веревки на 90°.

Известно, что если сила перпендикулярна направлению пути, то она работы не совершает. Вместе с тем, перемещая груз с помощью блока, человек выполняет работу, хотя прилагает силу, перпендикулярную направлению движения груза. Объясните кажущееся противоречие.

 ●85. И нуль и не нуль!

Если в космическом пространстве на тело действует постоянная сила, то совершается работа, равная скалярному произведению вектора силы на вектор перемещения тела. Если постоянная сила действует на тело, находящееся в среде, оказывающей сопротивление движению тела, и при этом тело дрижется равномерно, то работа должна быть равна нулю, так как к телу приложены две взаимно уравновешивающиеся силы, которые можно мысленно отбросить и считать, что на тело никакая сила не действует. Но этот вывод противоречит многочисленным примерам из повседневной практики. Как разрешить это противоречие?

 ○86. Как будет прыгать шарик?

Если уронить стальной шарик на морскую гальку, то он несколько раз подскочит. Иногда один из подскоков бывает рыше предыдущего (но не выше той высоты, с которой шарик уронили). Нет ли здесь противоречия с законом сохранения энергии?

 ●87. Как правильно рассчитать кинетическую энергию?

Камень массы m движется вместе с поездом со скоростью v₁. Какой кинетической энергией относительно Земли будет обладать камень, если его бросить по направлению движения поезда со скоростью v₂ относительно поезда?

Решение. Находясь в поезде, камень относительно Земли обладал кинетической энергией 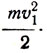. После того как его бросили, он относительно поезда стал обладать энергией 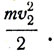Следовательно, относительно Земли его энергия равна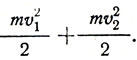

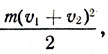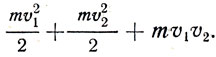Но, с другой стороны, скорость камня после броска относительно Земли равна v₁+v₂. Следовательно, его кинетическая энергия будет т. е. Как разрtшить противоречие полученных результатов?

 ●88. Могут ли две положительные величины в сумме дать нуль?

Поезд идет со скоростью v. С площадки заднего вагона человек бросает камень в направлении, противоположном движению поезда, со скоростью v относительно поезда. Абсолютная скорость камня (относительно Земли) стала равной нулю, и, следовательно, стала равной нулю и его кинетическая энергия относительно Земли. Таким образом, камень, который двигался вместе с поездом, до того как был брошен, обладал некоторой энергией. Человек, бросая камень, совершил работу и также затратил энергию. А в результате полная энергия камня равна нулю. Как разрешить противоречие: две положительные величины (кинетические энергии), складываясь, дают нуль?

 ●89. Удар шаров.

Несколько одинаковых стальных или костяных шаров подвешены на нитях, прикрепленных к одной доске (рис. 54). Шары в начальном положении касаются друг друга, и нити параллельны между собой. Что произойдет, если крайний левый шар № 1 отвести и отпустить? Удар считать центральным и идеально упругим.

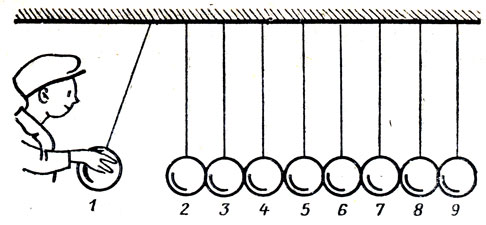
Рис. 54

Решение. Согласно закону сохранения энергии потенциальная энергия поднятого шара № 1 превратится сначала в кинетическую, затем в потенциальную упругой деформации шаров и снова в кинетическую энергию последнего (или последних) шара № 9. А эта энергия расходуется на его поднятие. При этом, если будет поднят один шар № 9, то на ту высоту, с которой упал шар № 1. Если (а это также возможно) отскочат шары № 8 и № 9, то на высоту, вдвое меньшую, чем та, с которой упал шар № 1.

Проделаем опыт и убедимся, что решение неверно. Во всех случаях отскакивает только один шар № 9 и поднимается на ту высоту, с которой падал шар № 1. В чем ошибка решения?

 ○90. Выполняется ли закон инерции на транспорте?

При торможении вагона троллейбуса, поезда, автобуса и т. п. наблюдается следующее явление: пассажиры сначала наклоняются вперед, а затем после остановки вагона резко (толчком) отклоняются назад. А ведь согласно закону инерции они должны были бы только наклониться вперед так, например, как это происходит с пассажирами, едущими в телеге или лодке при их резкой остановке. Как объяснить это кажущееся нарушение закона инерции в вагоне поезда и др.?

 ●91. Чем выше, тем теплее?

На второй этаж подняли вязанку дров. При этом дрова приобрели некоторую потенциальную энергию. Затем их сожгли в топке. Так как энергия исчезнуть не может, а в результате сжигания дров получается теплота, то выходит, что потенциальная энергия должна превратиться в тепловую. Таким образом, чем выше этажом сжигать дрова, тем в комнате будет теплее. В чем ошибка рассуждений и в какой вид энергии превратится потенциальная энергия вязанки дров, поднятой на второй этаж?