
Тема седьмая: Вопросы сопротивления материалов
Утверждения Галилея
("Беседы": а) стр. 56; б) стр. 75; в) стр. 73; г) стр. 230; д) стр. 231; е) стр. 275.)
а) Прежде всего нам надлежит рассмотреть, что соб-ственно происходит, когда ломается кусок дерева или другого тела, части которого прочно связаны между собою.
Для лучшего объяснения представим себе призму или цилиндр (см, рис. 16) из дерева или другого твёрдого материала, вставленный верхним концом А в свинцовую оправу, к нижнему концу которого подвешен груз С. Ясно, что каковы бы ни были сопротивление и связность частей твёрдого тела, раз они не бесконечно велики, они могут быть превзойдены силой растягивающего тела груза С, вес которого может быть увеличиваем по желанию, и твёрдое тело в конце концов разорвётся наподобие верёвки.

Рис. 16
Подобно тому как верёвке мы приписываем её сопротивляемость множеству составляющих её нитей пеньки, так и в дереве мы находим продольные волокна и нити, делающие его более прочным, нежели пеньковая верёвка такой оке толщины. Что касается цилиндров из камня или металла, то ещё большая связность их частей зависит от другой причины, отличной от нити и волокон.
б) Кто знает, не действуют ли в мельчайших частях также и мельчайшие пустоты и не они ли держат в связном состоянии части твёрдого тела.
Хотя эти пустоты имеют ничтожную величину и, следовательно, сопротивление каждой из них легко превозмогаемо, но бесчисленность их количества увеличивает сопротивляемость.
в) Возьмём для примера медную проволоку произвольной толщины и длины и прикрепим её за один конец.
Мы вправе сказать: всякая медная проволока, какова бы ни была её толщина, может держаться*, если длина её не превышает 4801 локтя.
* (Речь идёт о предельной длине проволоки, при которой она разорвётся под действием собственной тяжести.)
г) Теперь приступим к рассмотрению, в какой мере увеличивается момент собственного веса по сравнению с собственным сопротивлением излому призмы или цилиндра, когда последние, будучи расположены параллельно к горизонту, увеличиваются в длину: при этом найдём, что момент этот возрастает пропорционально квадрату длины.
д) В призмах или цилиндрах одинаковой длины, но разной толщины сопротивление излому возрастает в тройном отношении толщины или диаметра их основания.
е) Сопротивления двух цилиндров одинакового объёма и равной длины, один из которых полый, а другой массивный, относятся друг к другу, как их диаметры.
Разбор утверждений
Выше уже указывалось, что Галилей обратил свой взор не только в макромир вселенной, но и в микромир материи.
В первом случае он был вооружён подзорной трубой, а во втором случае ничего, кроме догадок, у него не было. Это и привело его к ряду заблуждений в тех случаях, когда он пытался объяснить природу явлений, связанных с прочностью тел.
Волокнистость вещества, вакуумные пузырьки в теле - все эти надуманные теории, однако, не помешали Галилею найти ряд количественных определений, во многом схожих с тем, чем пользуются и сейчас в учении о сопротивлении материалов.
Галилей отчётливо понимал разницу между растяжением и изгибом, но ещё не представлял себе природы таких деформаций, как скол, продольный изгиб и даже сжатие*.
* (Характерно, что Леонардо да Винчи, первый занимавшийся вопросами сопротивления материзлов, рассматривал лишь сжатие и продольный изгиб. Это позволяет утверждать, что по крайней мере в этой области до Галилея ничего не дошло от Леонардо да Винчи. )
Он считал, что во всех случаях при противодействии тела приложенной силе, нагрузка равномерно распределяется по всему сечению. При растяжении это предположение справедливо, но когда Галилей его применяет к изгибу, он допускает ошибку, которая приводит к неправильному представлению о распределении усилий по сечению. Исторический ход развития этих представлений виден на рисунке 17, На рисунке 17,а показано распределение усилий по Галилею,
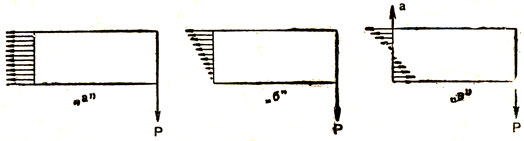
Рис. 17
В конце XVII в, Мариотт и Лейбниц уже указывали, что распределение усилий по сечению не равномерно и уменьшается сверху вниз (см. рис, 17,6). Современные представления по этому вопросу изображены на рисунке 17,5. Усилия по сечению в действительности не только не равномерны, но и имеют разное направление. В верхней части они способствуют растяжению, в нижней части - сжатию. Кроме усилий, нормальных к сечению, в действительности ещё имеет место добавочная сила Q, касательная к нему.
Все эти заблуждения не помешали Галилею установите целый ряд правильных положений в области сопротивления материалов, касающихся количественных зависимостей при оценке прочности материалов. Здесь он не имел предшественников и является одним из бесспорных основоположников этой области знаний.
В утверждениях Галилея, приведённых в пунктах "а" и "б", наряду с качественными рассуждениями о причинах, определяющих прочность тела, уже отчётливо формулируется представление о предельной нагрузке, разрушающей тело. Развивая эту мысль, Галилей показывает (см. пункт "в"), что для каждого материала существует его предельная длина, при которой тело ещё не разрывается под действием собственного веса. Галилей указывает, что эта длина зависит лишь от применённого материала, но не зависит от величины поперечного сечения. На первый взгляд это кажется парадоксальным. Это утверждение не только справедливо, но и показывает, что Галилей знал уже, как количественно связана величина поперечного сечения с допустимым усилием при растяжении.
В самом деле, предельная нагрузка для тела равна разрушающему напряжению, умноженному на величину поперечного сечения:
(1)
P = N · Q,
где N - разрушающее напряжение, Q - поперечное сечение. При действии собственного веса эта предельная нагрузка равна весу тела предельной длины l:
(2)
P = α · Q · l
где а - вес единицы объёма тела (удельный вес). Сопоставив уравнения 1 и 2, мы получим:
(3)
NQ = α · Q · l
или, исключив Q:
(4)
N = αl
в это уравнение не входит поперечное сечение, предельная длина тела зависит лишь от его прочности и не зависит от поперечного сечения.
Проверим, насколько близка к действительности приведённая Галилеем величина предельной длины медной проволоки.
Разрушающее усилие для проволоки красной меди обычно лежит в пределах 2200 - 3500 кГ/см3 в зависимости от её прокатки или термической обработки. Учтя, что удельный вес а ≈ 9, можно получить для предельной длины:
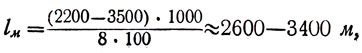
по Галилею же, учтя, что локоть равен примерно 0,45 м, эта величина должна быть равна:
l ≈ 4800 · 0,45 ≈ 2200 м.
Совпадение достаточно близкое.
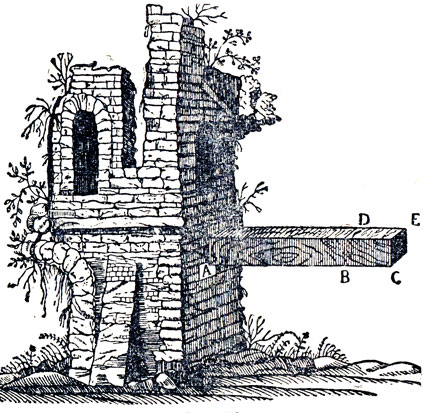
Рис. 18
Методика исследования прочности тела изгибающим усилиям у Галилея та же, что и при современном толковании этого вопроса. Он рассматривал (см. рис. 18) действие на сечение заделки А (наиболее опасное сечение)] момента силы:
(5)
M = P · l,
где Р - сила, l - длина тела.
Поэтому он правильно показал (см. утверждение "г"), что при равномерно распределённой нагрузке по длине усилие в сечении А будет зависеть от квадрата длины. Один раз длина войдёт в формулу при учёте момента, другой раз - при учёте нагрузки.
В утверждении, приведённом в пункте "д", Галилей говорит, что
(6)
P = k · D3 - для цилиндра,
(7)
P = l · α3 - для призмы квадратного сечения.
Современное учение о сопротивлении материалов даёт для предельной величины нагрузки выражение:
(8)
| P=n · | W | , |
| M |
где W - момент сопротивления площади поперечного сечения, М - момент действующей силы. Величина М зависит лишь от длины и не зависит от поперечного сечения, для величины же W даются следующие выражения:
(9)
W=0,0982D3 - для цилиндра,
(10)
| W = | a3 | для призмы квадратного сечения. |
| 6 |
Сопоставляя уравнения 8, 9, 10 с уравнениями 6 и 7, можно убедиться в справедливости утверждения Галилея.
Очень интересно утверждение Галилея, приведённое в пункте "е".
Здесь он показал глубокое проникновение в сущность процесса и положил начало инженерному подходу к выбору рациональных конструкций. Однако его утверждение не годится для тонкостенных труб.
Разберём этот вопрос подробнее. Утверждение Галилея может быть записано в виде:
(11)
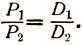
Для P1 и Р2 современное учение о сопротивлении материалов даёт для сплошного цилиндра:
(12)
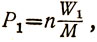
где W1 = 0,0982 D31
для полого цилиндра (трубы):
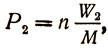
где
(13)
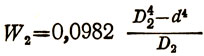
и
D2 - внешний диаметр трубы,
d - внутренний диаметр трубы.
Отсюда:
(14)
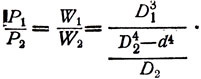
Из условия равенства площадей поперечного сечения (у Галилея "равенство объёмов и длин", что идентично равенству площадей поперечного сечения) следует:
(15)
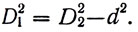
Вследствие этого уравнение 14 примет вид:
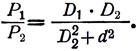
Сопоставляя уравнения 16 и 11, можно увидеть, что утверждение Галилея справедливо лишь для случая, когда D2 > d, т. е. для очень толстостенных труб.
Например, для трубы, у которой стенки составляют одну десятую диаметра, использование утверждения Галилея привело бы к ошибке в определении её прочности почти в два раза. Галилей, очевидно, производил опыты с толстостенными трубами* и поэтому этой ошибки не заметил. В самом деле, уже при толщине стенки, равной четверти диаметра, ошибка будет равна всего 30 процентам.
* (Например, со стволами медных или бронзовых орудий.)
Заключение
Галилей в области сопротивления материалов первым ввёл и обосновал численные соотношения для таких деформаций, как растяжение и изгиб. Он правильно указал влияние длины и площади поперечного сечения балки на величину сопротивления как для круглых, так и для квадратных сечений балки.
Галилей указал также, что применение трубчатых сечений позволяет значительно рациональнее использовать материал при одной и той же величине предельно допустимой нагрузки.
|
ПОИСК:
|