Какую скорость имеют молекулы?

У разных молекул скорости, конечно, разные. Чтобы вычислить давление газа, надо сделать какие- то предположения о том, как распределены молекулы по скоростям, т. е. какая доля молекул имеет заданную скорость.

Крениг (1856 г.) считал, что все молекулы движутся с одинаковой по величине скоростью и что каждая молекула движется в одном из трех возможных направлений, параллельных осям координат. Раньше Кренига (но позже Уотерстона) этой задачей занимался Джоуль (в 1851 г.). Он правильно понял связь между ударами молекул о стенки и давлением газа, но не смог получить верную формулу. Наконец, в 1857 г. Клаузиус, не оставляя еще предположения о равных скоростях, вывел новую формулу. Только через Два года (1859 г.) Максвелл пришел к правильному выводу.

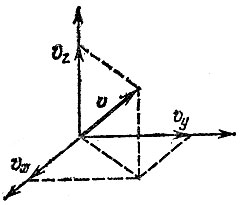
Рис. 13. Три компоненты скорости

Когда молекула сталкивается со стенкой и отскакивает от нее, стенка получает некоторый импульс. Предположим сначала, что молекула отражается от стенки упруго. Пусть ось z направлена перпендикулярно стенке, а оси х и у расположены в ее плоскости. Разложим скорость молекулы на составляющие по трем осям (рис. 13). При упругом ударе угол падения равен углу отражения, поэтому компоненты скорости v_x и v_y не изменяются. Компоненты же v_z при упругом ударе меняют знак. Таким образом, легко сообразить, что молекула изменит свой импульс (количество движения) на величину 2mv_z- Теперь надо сосчитать, сколько молекул ударится о стенку. Если расстояние между стенками, пересекающими ось z, равно l, то частица, ударившись о стенку, придет к ней в следующий раз через время, равное 2l/v_z, независимо от величины других компонент скорости. Значит, в единицу времени молекула ударится о стенку v_z/2l раз.

Так как с каждым ударом частица передает стенке импульс 2mv_z, то за единицу времени она передаст импульс mv²_z/l.

Чтобы получить величину давления, это выражение надо просуммировать по всем частицам (у каждой частицы своя vz) и разделить на площадь стенки, т. е. на l^2*:

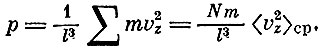
В этой формуле мы воспользовались определением среднего арифметического:

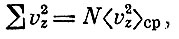
где N - общее число частиц.

^* (Для простоты мы считаем, что сосуд имеет форму куба объемом l³. Из соображений, о которых речь будет дальше, следует, что давление не может зависеть от формы сосуда - газ не "запоминает" форму.)

Последнее преобразование состоит в том, что мы заменим 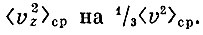. Так как 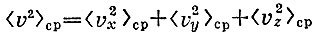и слагаемые справа одинаковы (мы с самого начала исходили из того, что движение хаотично и ни одно из направлений в сосуде не имеет преимущества перед другими), то

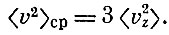
Заменяя еще отношение N/l³ на концентрацию частиц п, мы получим формулу Уотерстона для давления.

Задача, как видите, несложная, и Уотерстон ее решил верно. Крениг же предположил, что молекула при ударе передает стенке весь свой импульс, и получил результат, вдвое меньший^*.

^* (Так было бы, если бы молекула прилипала в стенке, а не отскакивала от нее.)

Можно, однако, подумать, что в выводе сделано одно очень важное упрощение: удар считался упругим. В действительности же это предположение, как ни удивительно, несущественно. Молекула может отразиться как угодно, но результат от этого не меняется. Предположение об упругом характере удара не меняет результат, зато делает вывод очень простым.

Такое замечательное свойство - независимость результата от закона отражения - является следствием теплового равновесия между газом и стенками сосуда, температура которых постоянна. От того, каким именно образом отражаются молекулы от стенки, окончательный результат - тепловое равновесие - не изменяется.

Можно проиллюстрировать это важное свойство равновесия одним примером. Предположим, что в сосуде с газом поставлена легкая подвижная перегородка, которая разделяет газ на две части так, что плотность газа и его температура в обеих частях сосуда одинаковы. Предположим, что одна сторона перегородки полированная, а другая шероховатая, так что законы отражения молекул от перегородки с обеих сторон заведомо различны. Если давления на перегородку с разных сторон оказались бы тоже различными, она сдвинулась бы, чтобы выравнять давление. Тем самым, оказалось бы, что в равновесии плотности газа с разных сторон перегородки различаются, хотя давления и температуры в обеих частях сосуда одинаковы. Но этот вывод находится в противоречии с уравнением состояния: давление и температура определяют однозначно плотность газа. Значит, давление не может зависеть от закона отражения молекул газа от стенок. Вот к каким общим заключениям приводит предположение о тепловом равновесии.