Энтропия

Пользуясь термометром, можно определить значение температуры любого тела. Правда, термометр показывает свою собственную температуру, а как она относится к температуре тела - не всегда просто выяснить. В нашей обыденной жизни мы часто говорим о температуре и большей частью забываем о сложных процессах, связанных с этим понятием. Научившись измерять температуру много лет назад, физики очень долго не могли понять, как температура связана с количеством теплоты. Очень трудно было догадаться, что у температуры есть связанная с ней величина - энтропия, увеличение которой, умноженное на температуру, определяет количество теплоты, полученной телом. Энтропия была открыта теоретически Клаузиусом и представляется одним из самых удивительных открытий, которыми столь богат XIX век.

Энтропия была введена в физику чисто теоретическим путем, так как не существовало прибора, которым ее можно было бы измерить. Нет даже способа сравнить энтропию двух разных систем, подобно тому как можно сравнивать температуру двух тел.

Нельзя, например, взять два сосуда с разными газами и сказать, какой из них имеет большую энтропию. Энтропию газа можно найти в таблицах, но нет прибора, подобного барометру или термометру, который бы показал величину энтропии.

Клаузиус пришел к понятию энтропии, пытаясь понять глубокий смысл исследований Карно. Карно, как мы уже знаем, доказал, что если между двумя "телами" - нагревателем и холодильником - существует обратимый термодинамический процесс, т. е. построена тепловая машина, которая совершает работу, отбирая от нагревателя теплоту Q₁ и отдавая часть этой теплоты Q₂ холодильнику, то Q₁ и Q₂ связаны с температурами T₁ и Т₂ нагревателя и холодильника пропорцией

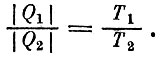
Это соотношение справедливо для любой тепловой машины, если только она идеальна, т. е. если ее можно заставить работать в "обратную сторону" так, чтобы, затрачивая ту же работу, она отбирала от холодильника количество теплоты Q₂ и передавала нагревателю количество теплоты Q₁

Написанную пропорцию лучше переписать так: Q₁/T₁=-Q₂/T. Знак минус поставлен как свидетельство того, что теплота отнимается от рабочего газа. Отсюда получается, что

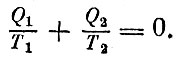
Мы получили выражение, похожее на закон сохранения. При работе тепловой машины по циклу Карно величина Q₁/T₁, "взятая" от нагревателя, равна величине Q₂/T₂, "отданной" холодильнику.

Сам Карно, как мы знаем, пользовался моделью теплорода. Эта модель должна была приводить к какому-то соотношению, выражающему сохранение гипотетической тепловой жидкости. Модель была бы приемлемой, если бы выполнялось соотношение типа |Q₁|=|Q₂|. Это означало бы, что теплота сохраняется, а работа совершается за счет перехода теплоты с более высокого уровня на более низкий.

Если бы температура была аналогом высоты, то работа, производимая машиной, должна была бы быть пропорциональной разности температур. Однако как мы только что видели, в обратимом процессе сохраняется не количество теплоты (или теплорода), содержащейся в теле, а другая величина, изменение которой равно изменению подведенной теплоты, поделенному на температуру тела.

Теплоту, участвующую в процессе, надо "поделить" на температуру, только тогда мы получим величину, сохраняющуюся в обратимом процессе.

Изменим обозначения и будем писать ΔQ₁ вместо Q₁ и ΔQ₂ вместо -Q₂ , подчеркивая, что речь идет о порции ΔQ₁, полученной рабочим газом, и Δ Q₂, потерянной им, Для цикла Карно

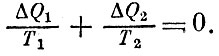
Клаузиус постулировал, что существует некоторая величина S, которая, подобно энергии, давлению, температуре, характеризует состояние газа. Когда к газу подводится небольшая порция количества теплоты Δ Q, то S возрастает на величину, равную

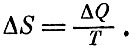
Величину S Клаузиус назвал энтропией.

После открытия Клаузиуса стало наконец ясно, почему было так трудно понять связь между теплотой и температурой. Оказалось, что нельзя говорить о количестве теплоты, заключенной в теле. Это понятие просто не имеет смысла. Теплота может переходить в работу, создаваться при трении и, вообще, никакой тенденции к сохранению не имеет.

В то же время точный смысл имеет понятие количества теплоты, переданного телу или же отнятого от него. Теплота может передаваться, но, вообще говоря, не сохраняется. Сохраняющейся величиной в обратимом процессе оказалась совсем новая величина, о существовании которой никто раньше не подозревал,- это и была энтропия Клаузиуса.

Посмотрим, например, что происходит с энтропией газа в цикле Карно.

Соотношение для цикла Карно, написанное выше, означает, что в обратимом цикле Карно энтропия рабочего газа на первом этапе цикла возрастает ровно настолько, насколько она уменьшается на третьем этапе. На втором этапе, на котором газ был изолирован и не получал тепла, его энтропия оставалась постоянной; также постоянной она оставалась и на четвертом этапе.

Таким образом, в обратимом цикле Карно энтропия рабочего газа не изменяется. Не изменяется она и при адиабатическом процессе.

К понятию энтропии можно прийти и другим путем, определив ее как величину, которая остается постоянной при адиабатическом процессе, подобно тому как температура постоянна при изотермическом процессе.

starslife.ru