Механика

Механика уже в XVIII в. становится самостоятельной научной дисциплиной математического характера. Ее связь с развитием физики не прерывается и в конце XIX столетия, когда механика вновь "офизичивается". Немалую роль в этом процессе сыграло открытие закона сохранения энергии. Вместе с тем существенную роль в развитии механических идей, имевших важное значение для физики, сыграли математика и механика первой половины XIX столетия. Уильям Роуан Гамильтон (1805-1865), Карл Густав Якоби (1804-1851) и Михаил Васильевич Остроградский (1801-1861) разработали вариационные принципы механики.

Ирландский математик и астроном Гамильтон подошел к вариационным проблемам механики, исследуя предварительно вариационную проблему оптики. Как известно, впервые Ферма в XVII в. показал, что законы геометрической оптики вытекают из принципа кратчайшего времени. Гюйгенс вывел эти законы с точки зрения волновой теории, с помощью сформулированного им принципа. Это указывает, что между "оптикой лучей" и "оптикой волн" существует тесная связь. Гамильтон, используя принцип Ферма, построил геометрическую оптику - "оптику лучей", введя специальную "характеристическую" функцию, которая с точки зрения волновой теории определяла время распространения волнового возмущения от источника до данной точки в неоднородной среде. "Теория систем лучей" Гамильтона была опубликована в 1827 г. Полученное им дифференциальное уравнение в частных производных первого порядка второй степени по форме существенно отличалось от линейного волнового уравнения в частных производных второго порядка. Но волновое уравнение в предельном случае бесконечно малой длины волны переходит в уравнение лучевой оптики.

От оптических задач Гамильтон перешел к задачам динамики. Применяя принцип наименьшего действия, Гамильтон разработал "общий метод динамики" в 1834-1835 гг. С этих пор в науку прочно вошла функция Гамильтона Н (гамильтониан), которая в случае связей, не зависящих от времени и движения в консерваторном поле, совпадает с полной энергией системы. Эта функция полностью характеризует систему. С ее помощью можно составить систему из 2f обыкновенных дифференциальных уравнений 1-го порядка (канонические уравнения механики), определяющих движение системы:

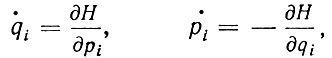
где q_i - обобщенные координаты, число которых равно числу степеней свободы f, определяющие конфигурацию системы; p_i - обобщенные импульсы системы.

В 1842-1843 гг. кенигсбергский профессор К. Якоби читал лекции по динамике, изданные в 1866 г. под этим названием. Якоби исходил из следующих принципов:

1. принцип сохранения движения центра тяжести;
2. принцип сохранения живой силы;
3. принцип сохранения площадей;
4. принцип наименьшего действия.

Касаясь теории Гамильтона, Якоби писал: "Особенно надо отметить те классы задач, для которых одновременно имеют место принцип живой силы и принцип наименьшего действия. Гамильтон заметил, что в этом случае задача может быть сведена к нелинейному дифференциальному уравнению в частных производных первого порядка. Если найдем одно его полное решение, то получаются тотчас все интегральные уравнения. Функцию, определяющуюся этим дифференциальным уравнением в частных производных, Гамильтон называет характеристической функцией".

Уравнение Гамильтона, о котором здесь пишет Якоби и которое ныне называется уравнением Гамильтона-Якоби, имеет вид:

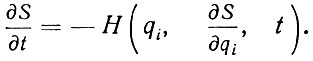
В правой части стоит функция Гамильтона Н (гамильтониан), в которой все импульсы p_i выражены через характеристическую функцию S (действие), подлежащую определению из этого уравнения посредством равенства

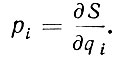
Для движения точки в консерваторном поле уравнение Гамильтона-Якоби принимает вид:

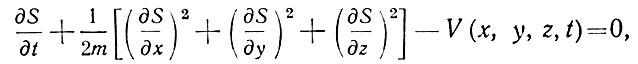
где V (x, y, z, t) - силовая функция поля. Это уравнение имеет форму, аналогичную с формой уравнения лучевой оптики Гамильтона. Таким образом, Гамильтон установил аналогию между движением материальной точки в силовом поле и движением луча света в среде с переменным показателем преломления. Эта оптико-механическая аналогия Гамильтона оставалась загадкой до XX в., когда она сыграла фундаментальную роль в создании волновой механики.

Русский математик М. В. Остроградский рассмотрел в 1848 г. принцип наименьшего действия в более общем, чем у Гамильтона, виде. В связи с этим принцип получил название принципа Гамильтона-Остроградского. Теоретическая физика XX в. высоко оценила принцип наименьшего действия Гамильтона-Остроградского. Она использовала его не только для решения динамических задач, но и для других физических задач, прежде всего задач электродинамики. Так, Лармор в 1900 г. показал, что если в выражении принципа наименьшего действия Гамильтона заменить кинетическую и потенциальную энергию магнитной и электрической энергией, то получатся основные уравнения электродинамики Максвелла. Однако физикой XIX в. принцип Гамильтона-Остроградского не был оценен. Механики предпочитали использовать привычные уравнения движения, а физики в это время были поглощены новым законом: законом сохранения энергии.

Уже в работах Гамильтона и особенно Якоби отмечалась роль "начала живых сил", т. е. закона сохранения энергии. Якоби отмечал, что этот принцип очень важен для проблемы центральных сил. "Принцип сохранения живой силы,- писал он,- охватывает большой класс задач, к которым, в частности, принадлежат задачи трех тел или более общая задача движения тел, которые взаимно притягиваются". "Чем больше мы проникаем в природу сил,- добавляет Якоби,- тем больше мы сводим все к взаимным притяжениям и отталкиваниям и тем важнее становится задача определения движения взаимно притягивающихся тел". Как мы видели, Гельмгольц выводил закон сохранения энергии, исходя из гипотезы, что все взаимодействия в природе носят характер центральных сил. В этом отношении механика центральных движений, и в особенности роль, которую в этой механике играет теорема живых сил, внесла свой существенный вклад в установление закона сохранения энергии. Интересно, что теорема живых сил, как это отмечает Якоби, впервые была "поднята на щит" в машиноведении. "Происхождение выражения "живая сила",- пишет Якоби,- объясняется тем значением, которое этот принцип имеет в машиноведении, основой которого он стал со времен Карно". (Якоби имеет в виду Л. Карно, знаменитого военного деятеля французской революции, отца С. Карно.) В этой дисциплине установлено, что половина живой силы, т. е. ¹/₂ ∑m_iv_i², равна работе машины, или, как выражаются в этих практических вещах, ¹/₂ ∑m_iv_i² есть то, что оплачивается в машине. Так протягивается нить от практики к величайшему теоретическому обобщению естествознания.

Учеником Якоби в Кенигсберге был выдающийся немецкий физик Г. Кирхгоф (1824-1887). В 1876 г. вышли его "Лекции по механике". Эта книга вызвала широкие отклики и послужила началом теоретических дискуссий о принципах механики. В предисловии к книге Кирхгоф писал: "Исходный пункт выбранного мной изложения отличается от обычного. Обычно механику определяют как науку о силах, а силы как причины, которые вызывают движение или стремятся вызвать. Конечно, это определение принесло большую пользу в развитии механики и оно еще останется в обучении этой науке, когда она поясняется примерами сил, почерпнутыми из опыта повседневной жизни. Но ему присуща неясность, от которой не могут освободить понятия причины и стремления. Эта неясность обнаруживается, например, в различии воззрений на то, что следует ли рассматривать закон инерции или закон параллелограмма сил как результат опыта, как аксиомы или предложения, которые могут и должны быть доказаны логически. При той строгости, которую в остальном допускает механика, мне казалось желательным избавить ее от темных мест, даже если это возможно только путем ограничения ее задачи. По этой причине я выдвигаю в качестве задачи механики описание происходящих в природе движений наиболее полным и простым способом. Тем самым я хочу сказать, что речь должна идти только о том, чтобы указать, как происходят явления, но не о том, чтобы определить их причины. Если исходить из этого и предположить представления о пространстве, времени и материи, то удается путем чисто математических соображений придти к общим уравнениям механики. Также и на этом пути имеют дело с понятием сила, хотя и не в состоянии дать его полного определения. Однако неполнота этого определения не влечет за собой никакой неясности, так как введение силы здесь является только средством упрощения способа выражения, именно только для того, чтобы выразить кратко уравнения, которые без помощи этого названия было бы трудно воспроизводить словами. Здесь достаточно, для устранения неясности, так определить силы, чтобы каждое предложение механики, в котором речь идет о силах, можно было перевести на язык уравнений и это осуществляется соответствующим образом".

Большой шум вызвало данное Кирхгофом определение задачи механики. Начало первой лекции воспроизводит это определение еще раз: "Механика - наука о движении; ее задачу мы определяем так: описать происходящие в природе движения полным и наиболее простым способом".

Венский физик и философ, основатель идеалистического направления в философии естествознания, получившего по его имени название "махизм", Эрнст Мах (1838-1916) полагал, что высказывание Кирхгофа является не чем иным, как выражением высказанной им еще в 1871 г. идеи, что "естествоиспытателю важно только экономическое описание фактов". Он утверждал, что его взгляды "не только более стары, но и более радикальны", чем взгляды Кирхгофа. Суть этих взглядов сам Мах передает следующим образом: "Понятие причины заменено здесь понятием функции; установление взаимной зависимости между явлениями, экономическое изображение фактов действительности провозглашено целью науки, а физические понятия - исполняющими средствами к этой цели".

В своей работе "Познание и заблуждение" Мах пишет: "Полное и простейшее описание Кирхгофа (1874), экономическое изображение фактического (Мах, 1872), "согласование мышления с бытием и согласование процессов мысли друг с другом" (Грассман, 1844) - все это выражает, с небольшими вариациями, ту же самую мысль". Приведя эту цитату из Маха в своей знаменитой книге "Материализм и эмпириокритицизм", В. И. Ленин писал: "Ну, разве же это не образец путаницы?" "Экономия мысли", из которой Мах в 1872 году выводил существование одних только ощущений (точка зрения, которую он сам впоследствии должен был признать идеалистической), приравнивается к чисто материалистическому изречению математика Грассмана о необходимости согласовать мышление с бытием! приравнивается к простейшему описанию (объективной реальности, в существовании которой Кирхгоф и не думал сомневаться!)"^*.

^* (В. И. Ленин, Сочинения, изд. 4, т. 14, стр. 158.)

Ленин безоговорочно причисляет Кирхгофа наряду с Гельмгольцем, Томсоном (Кельвином), Максвеллом, Герцем, Больцманом и Лорентцем к материалистам. Тот факт, что "Механика" Кирхгофа оказалась тесно связанной с философскими дискуссиями, не случаен. Она начинала длинную и сложную историю переосмысливания основных начал механики, как главы естествознания. В этой истории мы находим имена К. Неймана (1870), Штрейнца (1883), Маха (1883), Л. Ланге (1886), Г. Герца (1894-1895), Л. Больцмана (1897-1904) и, наконец, А. Эйнштейна (1905-1916).

Кирхгоф критиковал понятие силы как причины движения и рассматривал это понятие как формальное математическое выражение для произведения массы на ускорение. Само ускорение является функцией координат, таким образом, сила определяется конфигурацией системы Смысл понятия силы у Кирхгофа Больцман описывал следующим образом:

"Кирхгоф сам позже опять вводит слово сила, но не как метафизическое понятие, а лишь как сокращенное обозначение для определенных алгебраических выражений, постоянно встречающихся при описании движений".

Больцман с полным основанием замечает, что "Кирхгоф не предпринял какого-либо коренного изменения старой классической механики; его реформация была чисто формальной".

Более глубокое преобразование механики было предпринято Генрихом Герцем (1857-1894). Он умер 1 января 1894 г. В этом году, уже после его безвременной кончины, вышла в свет его книга "Принципы механики, изложенные в новой связи". Во "Введении" к этому труду Герц рассматривает три возможные системы построения механики. Одна из них - обычная классическая система ньютоновской механики, построенная на основных понятиях о пространстве, времени, массе и силе.

Герц критикует понятие силы. Он утверждает, что "в очень многих случаях силы, вводимые нашей механикой при рассмотрении физических вопросов, аналогичны работающим на холостом ходу колесам, исключаемым из общей системы повсюду, где требуется описать действительные факты". Физика, по его мнению, вынуждена была "чрезмерно заполнить мир самыми разнообразными силами: силами, которые сами никак не проявляются, и даже такими силами, которые действуют вообще только в самых исключительных случаях". Так, кусок железа, лежащий на столе, подвержен действию самых разнообразных сил: тяготения, магнитных, электрических - со стороны всех частиц Вселенной. И все же, несмотря на действие этих разнообразных сил, оно остается в покое. "Кого мы сможем убедить,- спрашивает Герц,- что мы говорим о действительных вещах, а не о картинах пылкого воображения?"

Герц приходит к выводу, что механика, которая исключает понятие силы, "более проста и в этом смысле более целесообразна".

Герц рассматривает далее другую систему механики, основанную на понятиях пространства, времени, массы, энергии. Герц считает эту систему более удовлетворительной, но все же изобилующей трудностями и неясностями. Так, использование принципа Гамильтона в качестве основного исходного принципа механики "не только ставит происходящее в настоящий момент движение в зависимость от последствий, которые могут выявиться в будущем, предполагая существование у неживой природы намерений, но, что еще хуже, он предполагает существование у природы бессмысленных намерений".

Герц отмечает далее трудности, связанные с вопросом о локализации потенциальной энергии. Для бесконечной Вселенной с бесконечным числом масс "существует и бесконечное число многочисленных форм потенциальной энергии в конечных количествах материи".

Третья система механики - это механика самого Герца. "От первых двух систем она отличается в основном тем, что исходит только из трех независимых представлений: из представлений времени, пространства и массы". Наряду с видимыми, ощущаемыми массами Герц допускает существование скрытых масс, отличающихся от обычных только тем, что они не ощущаются нами, но производят на массы такие же действия, как и обычные массы. "То, что мы называем обычной силой или энергией, представляет собой в нашем понимании не что иное, как действие массы и движения; однако оно не всегда может быть таким действием массы и движения, которое может быть доказано в грубо чувственной форме". Введя скрытые массы, Герц сводит механику к изучению движения масс, подчиненных связям. "Нам удалось,- пишет Герц,- сформулировать их (т. е. основные понятия механики: пространство, время, масса) эмпирическую, имеющую общее значение связь, в форме одного единственного закона, имеющего очень близкую аналогию с обычным законом энергии. Он может быть выражен, если пользоваться нашей терминологией, в следующей форме: каждое естественное движение самостоятельной материальной системы состоит в том, что система движется с постоянной скоростью по одному из своих прямолинейных путей".

Этот принцип Герца представляет собой дальнейшее развитие принципа наименьшего принуждения Гаусса и позволяет "геометризировать" механику, сводя решение задач динамики к геометрическим вариационным задачам. Тем самым Герц как бы предвосхитил вывод общей теории относительности, в которой также нет сил, а распределение масс определяет метрику четырехмерного пространства, времени, в котором частицы движутся по геодезической линии ("прямейший путь" Герца).

Механика Герца существенно отличается от механики Эйнштейна, оперируя с обычным эвклидовым трехмерным пространством, в котором движение системы определяется кинематическими связями со скрытыми массами.

В силу своей сложности механика Герца не получила практического применения, и механики продолжали и продолжают до сих пор пользоваться понятием силы, несмотря на методологическую неудовлетворительность этого понятия.

"Механику Герца,- говорил Больцман,- очень часто восхваляли, но я еще не видел никого, кто продолжил бы дальше найденный Герцем путь... Механика Герца мне больше кажется программой для будущего. Если бы когда-нибудь удалось объяснить непринужденно все процессы природы такими скрытыми движениями в герцевском смысле, то тогда старая механика была бы побеждена герцевской. До этого первая остается единственной, которая действительно способна представить в ясной форме все явления, не привлекая вещей, которые не только скрыты, но в которых даже нет никакого представления о том, как их следует мыслить".

Мы можем констатировать, что попытка изгнать силу из механики не удалась. Но критика основных понятий ньютоновской механики была полезна и необходима. Эта критика коснулась не только действительно неясного понятия силы, но и самой концепции абсолютного пространства и времени Ньютона.

В 1870 г. немецкий математик Карл Нейман (1832-1925), сын известного физика Ф. Неймана, написал книгу "Принципы теории Галилея - Ньютона". В ней он со всей ясностью выдвинул идею системы отсчета, в которой справедливы законы механики Ньютона. Эта система, которая сейчас называется "инерциальной" системой отсчета, Нейманом названа "системой альфа".

В 1883 г. вышло первое издание книги "Механика" Эрнста Маха, бывшего в это время профессором Пражского университета. Эта книга имела подзаголовок "Историко-критический очерк ее (механики) развития" и представляла философскую историю развития принципов механики. Эта книга от начала до конца проникнута махистской философией "экономного описания". Весьма удивительно, что Маху, занимавшемуся историей науки, не бросилась в глаза действительная историческая тенденция развития науки: приближение к все более точному отражению реальных взаимосвязей природы и он заменил ее фиктивной тенденцией "экономного описания". Современная физика с ее необычайно сложным и дорогостоящим оборудованием, труднейшим математическим аппаратом, требующим для своего усвоения огромной затраты умственного труда,- наглядная иллюстрация нелепости "экономической" тенденции, якобы проявляющейся, по Маху, в развитии науки.

В некоторых местах своей механики Мах остро и в общем правильно критикует догмы, укоренившиеся в науке. Критикуя концепцию абсолютного времени Ньютона как метафизическую, Мах указывает, что "время есть абстракция, к которой мы приходим через посредство изменения вещей".

"Абсолютное время,- пишет Мах,- не может быть измерено никаким движением, и поэтому не имеет никакого ни практического, ни научного значения, никто не вправе сказать, что он что-нибудь о таком времени знает, это праздное "метафизическое" "понятие". "В наших представлениях времени находят свое отражение самая глубокая и самая общая связь вещей".

В. И. Ленин писал, "... что Мах забывает свою собственную теорию и, начиная говорить о различных вопросах физики, рассуждает попросту, без идеалистических выкрутас, т. е. материалистически"^*. Это высказывание Ленина целиком относится к приведенным выше утверждениям Маха, в которых Мах высказывает правильную мысль, что нельзя рассматривать время независимо от вещей и их изменений. В объективном существовании вещей и их взаимосвязей Мах в данном случае не сомневается: "Мы не должны забывать того,- пишет он,- что все вещи неразрывно связаны между собой и что сами мы со всеми нашими мыслями составляем лишь часть природы". Это совершенно правильное, материалистическое утверждение. Но идеалистическая философия дает себя знать, и в конце концов Мах сводит понятия времени и пространства к "упорядочению рядов ощущений", лишая их объективного физического содержания, за что сокрушительно критикуется В. И. Лениным. Эта идеалистическая тенденция Маха мешала физикам разглядеть рациональное зерно в его критике.

^* (В. И. Ленин, Сочинения, изд. 4, т. 14, стр. 52.)

Такой же критике Мах подверг ньютоновскую концепцию абсолютного пространства, "существующего само по себе". "Об абсолютном пространстве и абсолютном движении никто ничего сказать не может, это чисто абстрактные вещи, которые на опыте обнаружены быть не могут",- пишет Мах. В связи с этим он анализирует опыт с вращающимся ведром, в котором, по мнению Ньютона, обнаруживается абсолютное вращательное движение. Мах указывает, что в этом опыте определяется вращение ведра относительно неподвижных звезд, а не относительно абсолютного пространства. "Можем ли мы удержать неподвижный сосуд с водой Ньютона, заставить вращаться небо неподвижных звезд и тогда доказать отсутствие центробежной силы?"- спрашивает Мах и отвечает: "Опыт этот неосуществим, сама мысль о нем вообще не имеет никакого смысла, ибо оба случая чувственно не могут быть отличены друг от друга. Я считаю поэтому оба случая за один и тот же случай и разложение Ньютона за иллюзию". Мах утверждает, что все основные принципы механики - это обобщение данных опыта об относительных положениях и движениях тел. Абсолютные движения Ньютона - иллюзия.

В том же 1883 г. вышла книга немецкого философа Людвига Ланге (1863-1936) "Историческое развитие понятия движения". В этой книге Ланге пользуется понятием "инерциальной системы" для систем отсчета, в которых выполняется закон инерции. По его мнению, такая система может быть реализована, если из некоторой фиксированной точки выпустить по трем не лежащим в одной плоскости направлениям свободные материальные точки. Если траектории этих точек - прямые линии, то система отсчета, образованная этими траекториями, будет инерциальной.

И в том же году вышло сочинение Штрейнца "Физические основы механики", в котором он также критиковал идею абсолютного равномерного прямолинейного движения. Штрейнц полагал, что для определения характера движения системы можно пользоваться гироскопом.

В 1899 г. на лекции, прочитанной в США, Л. Больцман коснулся этого вопроса. "При установлении законов движения,- говорит Больцман,- Ньютон рассматривает движение тела как абсолютное движение в пространстве. Но абсолютное пространство недоступно нашему опыту. Экспериментально всегда даются только относительные изменения положения тел. Таким образом, мы как раз в самом начале полностью выходим за пределы опыта, что, конечно, очень сомнительно в такой науке, которая ставит своей единственной задачей представить факты опыта. Эта трудность, конечно, не могла ускользнуть от такого гения, как Ньютон. Однако он полагал, что без понятия абсолютного пространства нельзя придти к простой формулировке закона инерции, имея целью выдвинуть его на первое место, и я полагаю, что здесь он также оставался правым, ибо сколько эта трудность ни освещалась, ни обдумывалась, однако едва ли был достигнут существенный прогресс. Нейман ввел вместо ньютоновского абсолютного пространства загадочное идеальное тело отсчета, тем самым так же, как и Ньютон, явно выходя за пределы опыта. Штрейнц поставил перед собой задачу, такого рода понятия или тела устранить, поскольку он учил, как можно посредством гироскопа, на который не действует никакая сила или действует известная сила, решить вопрос о том, имеет ли место для этой системы закон движения Ньютона, является ли она подходящей системой отсчета. Однако эти соображения Штрейнца кажутся мало полезными для обоснования механики, так как уже для законов движения вращающегося волчка и обсуждения вопроса о том, действует ли на него сила или нет, уже необходимо предположить знание законов движения Ньютона. Ланге пытался впрочем, формулировать закон инерции без какой-либо системы отсчета, только путем рассмотрения относительных движений. Хотя ему это и удалось, но таким сложным и многословным способом, что весьма трудно решиться поставить этот, с трудом обозримый закон, на место простой ньютоновской формулы. Само собой, что предложение Маха о прямых, определяемых всей совокупностью масс Вселенной, и предложение поставить на место абсолютного пространства мировой эфир, также выходят за пределы опыта, хотя, конечно, каждое в своем роде. Первое предложение опять-таки связано с чисто идеальным трансцендентным понятием; относительно последнего можно высказать то, что хотя его может быть и возможно экспериментально обнаружить, однако этого еще нет. Потому что для эфира имеет место совершенно иная механика, он должен, например, сам быть причиной инерции, а не подчиняться ей".

Такой неутешительный итог попытки ревизовать механику Ньютона объясняется тем, что эта ревизия потребовала коренного пересмотра представлений о пространстве и времени, как это было выяснено со всей обстоятельностью уже в XX в. Эйнштейном. Классическая ньютоновская механика продолжала успешно развиваться.

После работ Эйлера и Лагранжа, написавших уравнения динамики идеальной жидкости, Навье в 1822 г. попытался учесть силы вязкости. В 1845 г. в статье "О теории внутреннего трения в движущейся жидкости" Г. Стокс (1819-1903) вывел уравнения гидродинамики вязкой жидкости, получившие название уравнений Навье-Стокса. Так как в векторной форме эти уравнения сводятся к одному векторному уравнению, то сегодня говорят просто об уравнении Навье-Стокса. Из этого уравнения теоретически получались законы течения вязкой жидкости в капиллярных трубках, найденные экспериментально техником Гагеном в 1839 г. и французским физиологом и физиком Пуазейлем (1799-1869) в 1840 г. Эти законы имели важное значение для экспериментального определения коэффициента вязкости. В честь Пуазейля единица измерения коэффициента вязкости получила название пуаз. Стоке вывел закон движения шара в вязкой жидкости и формулу для коэффициента сопротивления движению шара в вязкой жидкости. Закон Стокса сыграл существенную роль в измерении такой физической константы, как заряд электрона. И поныне этот закон служит одним из основных методов определения вязкости.

В 1858 г. Г. Гельмгольц опубликовал статью "Об интегралах гидродинамических уравнений, отвечающих вихревым движениям". Он доказал, что наиболее общее движение элемента деформируемой среды слагается из трех компонентов:

1. поступательного движения;
2. вращения;
3. растяжения по трем взаимно-перпендикулярным направлениям.

Гельмгольц установил аналитическую характеристику вихря, нашел связь между угловой скоростью и линейной скоростью вращения. Доказанная им теорема гласила, что в идеальной жидкости интенсивность вихря не зависит от времени, т. е. вихри не могут ни возникать, ни исчезать. Развивая теорию вихрей, В. Томсон (Кельвин) в статье "О вихревом движении" (1869) ввел важное понятие циркуляции. Закон сохранения вихря можно выразить через циркуляцию следующим образом: циркуляция вдоль произвольного замкнутого контура, взятая в идеальной жидкости, не меняет своего начального значения с течением времени. Эта поразительная устойчивость вихревого движения навела В. Томсона на модель вихревых атомов. Попытки построить структуру эфира с помощью представления о вихрях предпринимались Мак Келлохом, В. Томсоном, Д. Лармором.

Связь между теоретической и технической гидродинамикой установили английский физик и инженер Осборн Рейнольде (1842-1912) и русский ученый и инженер Николай Павлович Петров (1836-1920). В своих работах "Экспериментальное исследование обстоятельств, определяющих, будет ли движение воды прямым или завихренным, и закон сохранения в параллельных каналах" (1883) и "Динамическая теория движения несжимаемой вязкой жидкости и определение критерия" Рейнольде исследовал условия превращения ламинарного (ползущего) движения жидкости по трубе в завихренное, турбулентное движение. Рейнольде установил, что критерием, позволяющим определить характер движения, является безразмерное число, называемое ныне числом Рейнольдса. Это число играет важную роль в экспериментальной гидродинамике. При моделировании движения того или иного аппарата в аэродинамической трубе необходимо соблюдать равенства чисел Рейнольдса для модели и аппарата.

Н. П. Петров в 1883 г. применил закон гидродинамики вязкой жидкости к построению гидродинамической теории смазки. В 1886 г. свои исследования по теории смазки опубликовал Рейнольде.

А. Зоммерфельд, который в 1904 г. продолжил исследования Петрова и Рейнольдса, писал, что эта проблема занимает одно из важнейших мест в области, связанной с "ползущими движениями". "В старых учебниках по технической механике,- писал Зоммерфельд,- трение цапфы в подшипнике относилось к вопросам сухого трения. Такое рассмотрение ничего общего с вопросами гидродинамики не имеет... Русский военный инженер Н. П. Петров был первым, который рассмотрел эту проблему с точки зрения вязких свойств смазки".

Но особенно тесная связь теоретической гидродинамики, точнее аэродинамики, с техникой была установлена в авиации.

Уже после франко-прусской войны 1870-1871 гг. начались эксперименты немецкого инженера Отто Лилиенталя (1848-1896) по полетам на аппаратах тяжелее воздуха. Лилиенталь построил большое количество планеров, исследовал влияние формы крыльев на подъемную силу и зависимость силы от угла атаки. Диаграмма связи между коэффициентом лобового сопротивления и коэффициентом подъемной силы получила в науке название "поляры Лилиенталя". Он изучал основы парения птиц. Его работа "Полет птиц как основа авиации" вышла в 1884 г. О. Лилиенталь трагически погиб 10 августа 1896 г. во время очередного полета.

В 1891 г. вышла работа знаменитого русского ученого, профессора Московского университета Николая Егоровича Жуковского (1847- 1921) под названием "О парении птиц". Разобрав различные точки зрения на природу парения птиц, в том числе и объяснение Лилиенталя, исследования которого он назвал "остроумными", Жуковский дал "полное решение задачи о скольжении птицы в покойном воздухе" и показал, "каким образом найденное движение видоизменяется в воздухе, текущем горизонтальными слоями разной скорости, дующем порывами или имеющем легкое восходящее движение". Жуковский рассмотрел различные траектории полета и показал, что птица в полете может описывать "мертвую петлю". Анализ Жуковского различных траекторий полета служит теоретической основой высшего пилотажа. "Мертвую петлю" впервые осуществил русский летчик П. Н. Нестеров в 1913 г.

В работе "О присоединенных вихрях", доложенной Московскому математическому обществу 15 ноября 1905 г., Н. Е. Жуковский дал знаменитую формулу для определения подъемной силы самолета, являющуюся основой аэродинамических расчетов. Согласно закону, найденному Жуковским, подъемная сила определяется циркуляцией вдоль замкнутого контура, обтекающего движущееся крыло. Вследствие вихреобразования эта циркуляция в пограничном слое, прилегающем к крылу, отлична от нуля. Таким образом, через два-три года после того, как поднялись в воздух первые самолеты братьев Райт, были найдены физические основы полета. Родиной авиационной теории стала Россия.

Поразительно, что почти за четверть века до появления работ Жуковского другой русский ученый-самоучка размышлял не более не менее как о полете в свободном (т. е. безвоздушном) пространстве. Гениальный самородок Константин Эдуардович Циолковский (1857-1935) создает основы межпланетного полета.

Утром 28 марта 1883 г. он записывает:

"Положим, что дана бочка, наполненная сильно сжатым газом. Если отвернуть один из ее тончайших кранов, то газ непрерывной струей устремится из бочки, причем упругость газа, отталкивающая его частицы в пространство, будет также непрерывно отталкивать и бочку. Результатом этого будет непрерывное изменение движения бочки". Рукопись "Свободное пространство", из которой взят этот отрывок, не была опубликована.

В 1894 г. в журнале "Наука и жизнь" была опубликована работа Циолковского "Аэроплан, или птицеподобная (авиационная) летательная машина". Циолковский снабдил в печати статью следующим примечанием: "Эта работа была написана еще в феврале 1894 г.; главные же выводы сделаны еще раньше (1890). Согласие их с последними опытами Лилиенталя и Максима побудило меня напечатать эту статью".

Содержание этой замечательной статьи показывает, как глубоко и всесторонне обсуждал Циолковский проблему полета на аппарате тяжелее воздуха. Он был в курсе всех исследований своих современников по этому вопросу: Лилиенталя, Жуковского, Марея, Максима и др. Академик А. А. Благонравов писал об этой работе Константина Эдуардовича:

"Поистине изумительно талантлива для своего времени работа Циолковского "Аэроплан, или птицеподобная (авиационная) летательная машина", опубликованная в 1894 г. в журнале "Наука и жизнь". В ней были предусмотрены почти все элементы конструкции самолета, разработанные позднее впоследствии рядом авиационных конструкторов, разрабатывавших и совершенствовавших самолеты. Здесь мы находим и четкую постановку вопроса о применении двигателей внутреннего сгорания в авиации, и предложение обтекаемой формы фюзеляжа и крыльев, и применение спаренных винтов противоположного направления вращения, колесное шасси, устройство рулей поворота и высоты и ... гидроскопический автопилот"^*.

^* (К. Э. Циолковский, Избранные труды. Серия "Классики науки". Изд. АН СССР, 1962, стр. 489-490.)

Академик Благонравов с полным основанием называет Циолковского основателем экспериментальной аэродинамики. 5 октября 1897 г. в письме к профессору А. А. Гершуну Циолковский описал свою аэродинамическую трубу, предназначенную для исследования сопротивления воздуха телам различной формы. Результаты исследований были опубликованы в "Вестнике опытной физики и элементарной математики" за 1899 г. в статье "Давление воздуха на поверхности, введенные в искусственный воздушный поток".

В 1901 г. Циолковский представил в Академию наук отчет о своих опытах по определению сопротивления воздуха. Краткое извлечение из этого отчета под заглавием "Сопротивление воздуха и воздухоплавание" было опубликовано в 1902 г. в журнале "Научное обозрение". В 1887 г. К.Э. Циолковский сделал доклад об управляемом металлическом дирижабле. Брошюра "Аэростат металлический, управляемый" вышла в 1892 г. Продолжение этой работы было издано в Калуге в 1893 г. Основные положения своих работ по управляемым аэростатам Циолковский изложил в статье "Возможен ли металлический аэростат", опубликованной в журнале "Наука и жизнь" за 1893 г.

Дирижаблестроение продолжало занимать Константина Эдуардовича и в последующие годы. Его статьи, книги, проекты по этой проблеме публиковались в 1896, 1897, 1898, 1900, 1901 и последующих годах вплоть до 1935 г., когда в газете "Коммуна" (Калуга) появилась последняя статья Константина Эдуардовича - "Поезд дирижаблей".

К. Э. Циолковский в полном смысле этого слова - отец советского дирижаблестроения. Но ведущая линия научно-технического творчества К. Э. Циолковского - это проблема межпланетных полетов. В 1893 г. появляется его фантастическая повесть "На Луне", в 1897 г.- "Грезы о Земле и небе". В том же 1897 г. он вывел свою знаменитую формулу, устанавливающую связь между скоростью ракеты, скоростью истечения газовой струи, массой ракеты и массой израсходованных взрывчатых веществ:

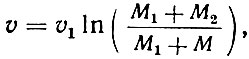
где v - скорость ракеты, v₁ - скорость истечения частиц газа, М₁ - масса ракеты без топлива, М₂ - масса топлива в начале движения, М - масса топлива в момент достижения скорости v.

В 1903 г. вышел классический труд К. Э. Циолковского "Исследование мировых пространств реактивными приборами", в котором впервые была опубликована эта формула. Начало борьбы за завоевание космоса было положено этой знаменитой работой.

Из сказанного следует, что в последней трети XIX столетия механика тесно связывается с передовой техникой и физикой. В самой механике важную роль начинает играть физический эксперимент. Этот процесс "офизичивания" и "отехничивания" механики продолжается и в XX в. Вместе с тем механика прокладывает пути важным физическим и техническим применениям. Так, в 1892 г. выдающийся русский ученый A. M. Ляпунов (1857-1918) опубликовал свою докторскую диссертацию "Общая задача об устойчивости движения", в которой содержались важные идеи, нашедшие свое применение в проблемах нелинейной радиотехники и автоматики в XX в.

С повышением быстроходности и мощности паровых машин особую остроту приобрела проблема автоматического регулирования. В Англии в 1868 г. работало около 75 000 регуляторов Уатта, и исследование их действия стало насущной необходимостью.

Русский финансист и математик И. А. Вышнеградский (1831-1895), словацкий инженер Аурель Стодола (1859-1942) внесли существенный вклад в решение проблемы автоматического регулирования. Работа И. А. Вышнеградского "О результатах прямого действия" появилась в 1876 г. Теория регуляторов непрямого действия, в которых регулирование осуществляет специальный двигатель-сервометр, была разработана А. Стодолой в работах "О регулировании турбин" (1893-1894) и "Принцип регулирования Сименса и американские инерционные регуляторы" (1899).

В исследованиях Вышнеградского и Стодолы были заложены основы линейной теории автоматического регулирования. Современная нелинейная теория представляет собой дальнейшее развитие этой важнейшей отрасли современной науки и техники.

Итак, механика к началу XX в. выдвинула ряд важнейших научных и технических проблем, которые были решены наукой XX в. Сюда относятся проблемы основных понятий механики: пространства, времени, массы, силы. Механика приступила к решению задач гидро- и аэродинамики, имеющих огромное значение для развития авиации. Была поставлена проблема космических полетов. И, наконец, были поставлены задачи, имеющие существенное значение для современной радиофизики и автоматики.