Система единиц

Мы остановимся теперь на важных заслугах Гаусса в истории физики. Сюда относится в первую очередь установление рациональной, так называемой абсолютной системы единиц.

Измерение величины - это процесс сравнения её с определённой однородной величиной, принятой за масштаб сравнения. Результат измерения выражается именованным числом, отвлечённая часть числа выражает отношение измеряемой величины к масштабу, наименование указывает на принятый масштаб (локоть, аршин, фут, метр и т. д.). Чтобы получить это число, надо, с одной стороны, выбрать масштаб, с другой - выработать процедуру измерения. Фактически дело обстоит таким образом, что измерение любой физической величины сводится к пространственному отсчёту (движение "зайчика" на шкале зеркального гальванометра, движка в схеме мостика, нониуса в спектрометре, стрелки секундомера и т. д.). Правила и манипуляции, связывающие измерение данной величины с таким отсчётом, в большинстве случаев настолько сложны, что их обычно не развёртывают, а скрывают за условным наименованием единицы. Так как, однако, физические законы выражаются уравнениями, в которые в качестве алгебраических величин входят числовые значения измеренных физических величин, то требование логического соответствия правой и левой части равенств при произволе в выборе единиц приводит к загромождению формул переводными множителями, имеющими сложное наименование и численное значение, меняющееся с изменением масштаба той или иной входящей в формулу величины.

При полном произволе в выборе масштаба, методики измерений, нетрудно представить, какой хаос царил в экспериментальной физике, как трудно было сравнивать результаты измерений различных наблюдателей, если сами измерения носили сугубо относительный характер. Дело особенно осложнилось, когда началось количественное исследование электрических и магнитных явлений. И вот Гаусс в своей знаменитой работе, появившейся в результате совместной с Вебером работы по магнитным измерениям "Intensitas vis magnetical terrastris ad mensuram absjlutam revocata" ("Интенсивность магнитной силы, выраженной в абсолютной мере"), даёт основания рациональной, так называемой абсолютной системы единиц. Согласно принципиальным установкам Гаусса, все физические величины, подлежащие измерению, можно разбить на две группы: основные и производные.

Дух XVIII в. ярко отразился в установках Гаусса. Это, с одной стороны, принятие за основу мер - метрическую систему, с другой - мысль о сведении всех физических явлений к движениям и силам, их производящим. Понятно, что основными единицами в системе Гаусса являются единицы механики: длины - миллиметр, времени - секунда.

Единица магнитной силы, т. е. количества магнетизма,- это такое количество магнетизма, которое отталкивает равное ему количество, помещённое на расстоянии 1 мм, с силой, равной единице.

Таким образом, единица силы в системе Гаусса равна 10^-4 дины, единица магнетизма равна 10^-3 единиц в системе CGSM, единица напряжённости поля 0,1 эрстеда. Правило, по которому устанавливается размерность производных единиц, заключается в том, что коэффициенты формул должны быть возможно проще, обычно равными единице. Так, например, вышеприведенная единица магнетизма получается из основных, если в формуле Кулона для взаимодействия магнитных масс в пустоте положить коэффициент пропорциональности равным единице. Таким же образом единицы электрических величин могут быть получены из закона Кулона для электрических взаимодействий. Но тогда в формулах, выражающих связи между магнитными и электрическими величинами (например в законе Био-Савара), непременно появятся подлежащие опытному определению коэффициенты, обладающие определённой размерностью и численным значением. Ниже мы рассмотрим, к каким результатам привели эти определения.

Понятно, что Гаусс считал необходимым фундировать свою систему надёжно. Им, совместно с Вэбером, были разработаны конструкция магнитометров и метод измерения магнитных полей. В своих магнитометрах Гаусс заменил укрепление стрелки на оси подвесом на нити, как унифилярным, так и бифилярным. Это в сильной степени повысило чувствительность прибора. Методика, разработанная Гауссом, представляет большой принципиальный интерес, так как опирается на действительно физически определимые величины: напряжённость поля (магнитная сила) и магнитный момент. В методе Гаусса количество магнетизма (магнитная масса) выступает как вспомогательная величина.

Напомним кратко идею Гаусса, ограничиваясь первой степенью приближения в подсчётах.

Если допустить, что размеры магнита магнитометра настолько малы, что на всём его протяжении исследуемое поле Н можно считать однородным, и, если далее пренебречь направляющей силой нити подвеса, то в положении, при котором магнит образует угол φ с направлением поля Н, на него действует момент, равный МН sin φ, где М - магнитный момент. Этот момент равен скорости уменьшения вращательного импульса магнита, т. е. 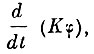где К - момент инерции магнита.

Таким образом,

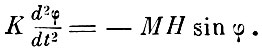
При малых углах

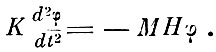
Решение этого уравнения имеет вид

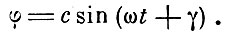
Период колебания магнита будет равен таким образом

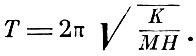
Момент инерции системы можно определить динамическим экспериментом заранее и таким образом определить отсюда величину А = МН.

Теперь магнит используется, как источник магнитного поля. Его ось устанавливается перпендикулярно магнитному меридиану. Вспомогательная стрелка m помещается на продолжении оси магнита на запад или восток (первое гауссово положение). Под действием поля магнита М и поля Н она отклонится от меридиана на угол φ, определяемый в первом приближении равенством

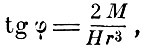
где r - расстояние центров магнита и стрелки. Затем вспомогательную стрелку помещают к северу или югу от магнита (второе гауссово положение), тогда стрелка будет образовывать с меридианом угол φ', определяемый равенством

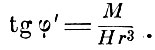
Эти измерения дают возможность определить отношение 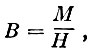и, таким образом, найдутся

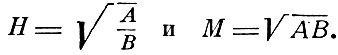
Гаусс воспользовался своим методом для проверки закона Кулона. Соотношение tg φ = 2 tg φ', получаемое из формул

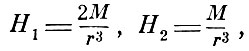
является следствием закона Кулона для взаимодействия точечных полюсов. Гаусс предположил, что полюса взаимодействуют с силой, обратно пропорциональной rⁿ, где n - целое число. Тогда вычисления приводят к следующим результатам:

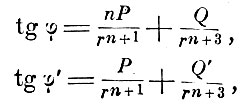
где P, Q, Q' - величины, характеризующие магниты и поле, но не зависящие от r. При достаточно больших r и малых φ и φ'

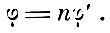
Гаусс измерял φ и φ' при 15 различных r, от 1,1 м до 4 м, причём оказалось, что n = 2. Например, для r = 3,5, φ = 6'56,9", φ' = 3'28,9". Для проверки он положил в формулах для tg φ и tg φ' n = 2 и вычислил коэффициенты Р, Q, Q' по способу наименьших квадратов. Для определения углов получились эмпирические формулы

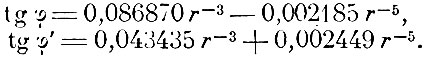
Углы, вычисленные по этим формулам, находятся в хорошем совпадении с экспериментальными определениями.

Таким образом, закон Кулона подтверждается. Появившаяся в 1839-1840 гг. в "Результатах наблюдений магнитного общества" работа Гаусса "Общие предложения о силах притяжения и отталкивания, действующих обратно пропорционально квадрату расстояния", представляет систематическую теорию потенциального силового поля. Известная из электростатики "теорема Гаусса" доказывается в этом труде.

Пуассон, Грин, Гаусс явились, таким образом, основоположниками математической теории электростатики и магнитостатики. Эти задачи привлекали внимание математиков и физиков в течение всего XIX в.