Дальнейшие успехи экспериментальной волновой оптики

Итак, явление дисперсии в конечном счёте послужило успеху волновых представлений в оптике, хотя впереди намечались и большие трудности в связи с объяснением происхождения спектров. С другой стороны, основные положения оптики Френеля - Юнга получили всё большее подтверждение и развитие в тех областях оптических явлений, которым они обязаны были своим происхождением.

Основные интерференционные опыты Френеля и Юнга, как известно, относятся к классу тех интерференционных явлений, которые локализованы в пространстве; точки, в которых происходит погашение света или усиление интенсивности, лежат на гиперболоидах с фокусами в источниках.

Новые видоизменения этих основных экспериментов принадлежат Ллойду (1834), Билле (1858). В опыте Ллойда интерференция происходит от источника S, расположенного в плоскости, весьма близкой к плоскости зеркала, и его изображения в этом зеркале S'. Таким образом, прямые пучки интерферируют с отражёнными. Так как здесь будет наблюдаться только одна половина интерференционной картины, то, чтобы сделать видимой центральную часть, помещают на пути прямых лучей пластину, вызывающую смещение интерференционной картины. Центральная линия, как это и следует из теории Юнга о потере полуволны, при отражении оказывается чёрной.

Значительно продвинулось изучение того класса явлений, с которого и началось изучение интерференции, а именно цветов тонких пластинок. Пуассон в 1823 г. указал, что необходимо учитывать при расчёте интерференционной картины многократные отражения луча внутри пластины. Расчёт был им проведён для случая, когда разность ходов равна целому числу полуволн. Эри в 1834 г. разобрал общий случай. Если амплитуда падающей волны 1, амплитуда волны, отражённой от первой поверхности а, амплитуда волны, преломлённой при переходе из среды в пластинку b, а' -доля отражённой волны при отражении от второй поверхности, b'- доля преломлённой волны при переходе из пластинки в среду, b - запаздывание фазы луча, испытавшего одно внутреннее отражение относительно первого отражённого луча. Тогда для амплитуды суммарного колебания в отражённом свете получается выражение

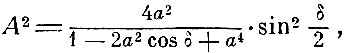
при этом принимается во внимание выражение

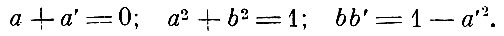
Эти выражения получаются из общей формулы, если положить толщину пластинки, равной нулю; первое из них выражает закон Араго о равенстве коэффициента отражения при переходе из первой среды во вторую, и наоборот, и закон Юнга об изменении фазы при отражении от более плотной среды.

Позднее (1849) Стоке вывел эти соотношения, пользуясь принципом обратимости. При этом Стоке пытался обобщить свой вывод и на общий случай изменения фазы (а не только юнговское изменение на π), но полученные им формулы для интенсивности не приводят к правильным результатам для тонких пластинок.

Однако эти формулы Пуассона - Эри находятся в большем соответствии не с случаем колец Ньютона и аналогичных ему случаев, так называемых линий равной толщины, а с открытым позднее Гейдингером (1855) явлением линий равного наклона. Эти линии наблюдаются на строго плоскопараллельных пластинках при аккомодации глаза на бесконечность. Гейдингер наблюдал их на пластинке слюды толщиной 0,2 мм, освещенной пламенем натрия. Проверить наблюдения Гейдингера было нелегко, и линии равного наклона были вновь открыты Луммером в 1884 г.

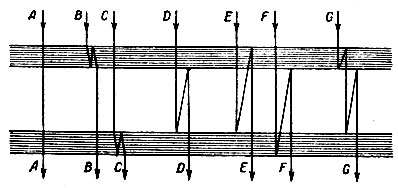
Рис. 243. Полосы Брюстера

В 1817 г. Брюстер наблюдал интерференцию от двух плоскопараллельных пластинок, наклонённых под малым углом друг к другу. Видоизменение этого эксперимента представляет установка Жамена (1857) - интерферометр Жамена. Эта установка открыла возможность применения интерференции для точных измерений (показателя преломления газов и др.).

Опыты Юнга и Френеля проводились с белым светом, что приводило к крайнему ограничению картины (до десятка полос) и не давало возможности точного измерения длины волн.

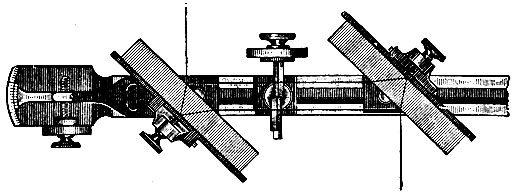
Рис. 244. Интерферометр Жамена

Брюстер (1828), применяя освещение спиртовой лампой с натрием, наблюдал всё поле, покрытое полосами. Физо и Фуко исследовали предельное число интерференционных полос в однородном свете, или, что то же самое, предельную разность хода. Метод, которым они пользовались, заключался в следующем. Система зеркал Френеля освещалась источником белого света. На экране наблюдалась интерференционная картина, в экране была щель, пучок лучей, выходивший из щели, падал на призму, причём щель устанавливалась на центральную белую полосу, так что на призму падал узкий пучок белого света, который развёртывался в спектр. Затем одно из зеркал передвигалось вперёд параллельно самому себе. Когда разность хода достигла полуволны фиолетового света, в фиолетовой части спектра появлялась тёмная линия, которая при дальнейшем перемещении зеркала начала сбегать к красной части, затем в фиолетовой части появлялась вторая, затем третья и т. д.

Физо и Фуко насчитали таким путём до 4000 полос, прошедших через красную часть спектра (1849). В следующем году, экспериментируя с толстыми пластинками, они получили предельную разность хода в 7394 длины волн. "Наличие этих явлений взаимного влияния двух лучей в случае большой разности хода интересно для теории света, поскольку оно выделяет в излучении последовательных волн неизменную регулярность, какой до сих пор не обнаружило 'ни одно явление" ("Ann. de chimie et de physique", XXX, 146, 1850).

В 1863 г. Физо экспериментировал с кольцами Ньютона, причём установка освещалась натриевым светом. Линзу в этой установке можно было медленно перемещать параллельно горизонтальной пластинке. Вследствие такого перемещения кольца стягивались к центру, где и исчезали. Физо считал число исчезнувших колец. Когда прошло 500 колец, интерференционная картина исчезла. Однако при дальнейшем перемещении она вновь появилась, и когда прошло 1000 колец, достигла прежней резкости. При 1500 колец она снова исчезла и т. д. Этот опыт дал возможность Физо установить, что:

1. интерференция ещё возможна при разности ходов 50000 к натриевого света и
2. свет натрия неоднороден, а состоит из двух сортов лучей, коим соответствуют длины волн λ₁ и λ₂ причём приблизительно 1001 λ₁ = 1000 λ₂ и 500 λ₂ = 500 λ₁ + ¹/₂ λ₁.

Так обнаружилась высокая разрешающая способность интерференционных установок, которая впоследствии была использована в интерференционных спектроскопах.

Таким образом, и интерференционные опыты, и решётки Фраунгофера^*, и спектроскопы Бунзена - Кирхгофа способствовали укреплению фундамента волновой теории, доставляя средства всё более надёжного и точного определения длин волн. С другой стороны, развитие кристаллооптики и исследование явлений отражения и преломления давали твёрдое доказательство поперечности световых волн. Были созданы аппараты, позволяющие анализировать и измерять поляризацию лучей. Вместе с тем оптический анализ стал оказывать серьёзные услуги кристаллографии. Зеркало и стеклянная стопа были первыми поляризаторами и анализаторами в аппарате Био (1814) и Нёрренберга (1833).

^* (Волновую теорию решётки дал в 1835 г. Шверд. Бабине ещё в 1829 г., основываясь на свойствах решётки, предложил выбрать длину волны, как естественную, неизменную единицу длины.)

В 1828-1840 гг. появились описания исследований с призмой Николя, которая и поныне является наиболее совершенным поляризатором и называется по имени её изобретателя николем.

Эти приборы и используются в полярископах и поляриметрах. Они дают возможность однозначно определить, поляризован ли линейно данный пучок света, и установить направление плоскости поляризации. Можно также определить в пучке с частичной поляризацией долю поляризованных лучей и определить направление их плоскости поляризации. Таковы полярископы Араго, Желле, Савара.

Для более точного фиксирования плоскости поляризации применяются конструктивные видоизменения поляризационных устройств (например, в "полутеневых" поляриметрах Желле разрезается призма Николя).

Приведём в качестве примера подобных устройств, относящихся к рассматриваемому нами периоду, поляриметр Савара (1840). В этом поляриметре основной частью является пластинка Савара. Пластинка Савара представляет собой две кварцевые пластинки, вырезанные под углом 45° к оптической оси и сложенные так, что плоскости их главных сечений взаимно перпендикулярны. Если на такую пластинку падает пучок лучей, содержащий примесь линейно-поляризованных лучей, то при рассматривании через николь будут наблюдаться полосы хроматической поляризации. Этих полос не будет видно только в том случае, если пучок, входящий в прибор, не поляризован или поляризован по кругу. Прибор обладает высокой чувствительностью.

Полярископы не дают возможности определить характер поляризации. Установить, является свет естественным или круговым, частично поляризованным или поляризованным эллиптически, можно только с помощью дополнительных приспособлений, позволяющих обнаружить фазовые соотношения между компонентами.

Рассмотренный нами в X главе ромб Френеля даёт возможность проверки таких соотношений. Аналогично ромбу будет действовать так называемая пластинка четверть волны (¹/₄ λ), вырезанная из одноосного кристалла параллельно оптической оси и толщина которой подобрана таким образом, что разность фаз обыкновенного и необыкновенного луча по выходе из пластинки равна ^π/₂.

Пластинка Савара принадлежит к числу пластинок, изменяющих разность фаз между компонентами. Приспособления, позволяющие менять разность фаз между компонентами, называются компенсаторами. Компенсатор Бабине (1794-1872) состоит из двух кварцевых призматических пластинок с весьма малым преломляющим углом. Обе пластинки вырезаны параллельно оси, но в одной ось параллельна преломляющему ребру, во второй перпендикулярна; таким образом,плоскости главного сечения обоих

пластинок взаимно перпендикулярны. При симметричном положении пластин разность фаз в центральной части между обыкновенным и необыкновенным лучом равна нулю. Смещая при помощи винта одну пластину вдоль другой, мы вводим разность фаз, определяемую разностью толщин пластин в центральной части.

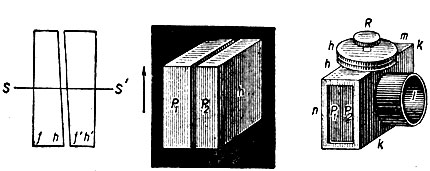
Рис. 245. Компенсатор Бабине

Браве (1855) сконструировал компенсатор, представляющий комбинацию двух компенсаторов Бабине, расположенных антипараллельно друг другу.

Теперь оптика располагала средствами полного анализа света. В частности, весьма важно было исследовать поляризацию света при отражении. Согласно формулам Френеля, линейно-поляризованный свет после отражения оставался линейно-поляризованным. При угле Брюстера естественный свет превращается в линейно-поляризованный. Эри в 1833 г. нашёл, что эти соотношения не выполняются точно для сильно преломляющих сред, как, например, алмаза.

Жамен в ряде исследований, продолжавшихся с 1845 по 1851 г., показал, что при отражении возникает, как правило, некоторая разность фаз и, следовательно, линейно-поляризованный свет превращается в эллиптически поляризованный. Только для n = 1,42 формулы Френеля приблизительно удовлетворяются. Если n>1,45, то луч, поляризованный в плоскости падения, отстаёт от луча, поляризованного в перпендикулярной плоскости, при n<1,40 соотношение будет обратным.

Особенно сильная эллиптичность наблюдается при отражении от металлических поверхностей. Ещё Малюс заметил, что отражением от металлических поверхностей нельзя получить полной поляризации. При некотором угле падения i степень поляризации наибольшая. Этот угол называется главным углом падения (для стали i = 75°, серебра 73°, ртути 78° и т. д.), величина этого угла зависит от длины волны падающего света.

При главном угле падения разность фаз между обоими компонентами светового вектора достигает 90°. Эллиптическую поляризацию при отражении исследовал Бабине (1838), позже (1867) Квинке. Стоке (1853) связал сильную отражательную способность металлов с их поглощательной способностью. Анилиновые краски с металлическим блеском отражают те лучи, для которых они наименее прозрачны.

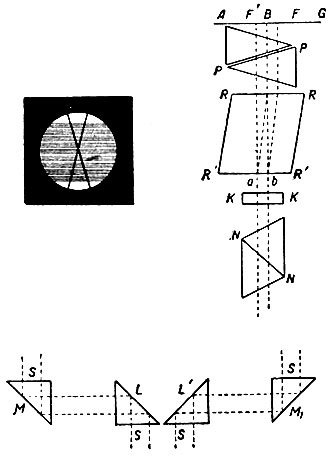
Рис. 246. Фотометр Вильда

Полярископы нашли себе применение и в фотометрии. В 1853 г. появился поляризационный фотометр Бабине, через три года фотометр Вильда, а в 1861 г.- поляризационный фотометр Цельнера для астрофотометрии. Мы не будем, однако, останавливаться на описаниях этих приборов, ограничимся только воспроизведением схемы фотометра Вильда.

Успехи поляриметрии нашли применение и в приложениях. Мы уже говорили о кристаллографии, где начиная с сконструированного в 1844 г. Амичи прибора, большое значение приобретают поляризационные микроскопы.

Развилась и сахариметрия. Сахариметры Био (1840) и Митчерлиха (1844), в которых трубка с испытуемым раствором помещалась между двумя скрещенными николями, не давали точных результатов. Более надёжными оказались сахариметры Солейля (1845), Желле (1860) и Вильда (1864).

В сахариметре Солейля применяется бикварц, т. е. пластинка, сложенная из двух полупластинок кварца одинаковой толщины, из которых одна вращает свет влево, другая вправо. Компенсирующее устройство состоит из пластинки кварца, вращающего вправо, и двух кварцевых клинообразных пластинок, вращающих влево. В сахариметре Желле для точного установления направления плоскости поляризации служит его полярископ, в сахариметре Вильда - пластинка Савара.