Теории света

Вместе с успехами экспериментальной оптики развивалась и оптика теоретическая. С одной стороны, стояла задача разработать математическую схему, описывающую оптические явления, с другой - открыть внутренний механизм этих явлений и связать

разнообразные, изученные экспериментально факты единой точкой зрения.

Первая задача с успехом начала разрабатываться уже в XVIII в. на основе понятия луча. Геометрическая или лучевая оптика достигла в рассматриваемый период выдающихся результатов. Можно проследить три основных пути, по которым приходили к этим результатам. Прежде всего путь чисто геометрический, разрабатываемый блестящими геометрами XIX в.

Математическая проблема формулировалась как проблема преобразования пучков прямых в одном пространстве (пространстве объектов) в пучки в другом сопряжённом пространстве (пространстве изображений). Таковы были, например, исследования Куммера (1859 г.).

В качестве примера приведём некоторые теоремы, полученные в этом направлении. В 1808 г. Мал юс доказал следующее предложение, носящее название "теоремы Малюса".

"В изотропных средах изогенный пучок лучей, т. е. лучей, вышедших из одной точки или нормальный к одной и той же поверхности, остаётся после любого числа отражений или преломлений нормальным к одной и той же поверхности S".

Жергонн в 1823 г. доказал теорему; "Любое число отражений и преломлений пучка лучей можно заменить одной Операцией отражения или преломления, смотря по тому, будет ли конечная среда тождественна с первой или от неё отличной".

Задача практической оптики заключается в изготовлении оптических систем, дающих изображения без искажений. Таким образом, в идеальной оптической системе гомоцентрический пучок лучей должен преобразовываться в гомоцентрический же. Штурм в 1848 г. доказал астигматизм пучков. Он доказал, что, вообще говоря, бесконечно малый параллельный пучок лучей, вышедший из оптической системы, будет сходиться в двух фокальных линиях и что эти линии расположены в изотропной среде в взаимно перпендикулярных плоскостях.

Гаусс в своих "Диоптрических исследованиях" (1846) пошёл по другому пути. Он рассматривал центрированную оптическую систему, у которой центры всех преломляющих и отражающих поверхностей лежат на одной прямой оптической оси. Изображения осуществляются с помощью тонких пучков, наклонённых под весьма малыми углами к оптической оси (параксиальные лучи).

Гауссовская теория параксиальных лучей и составляет другое направление геометрической оптики. Центрированная оптическая система, по Гауссу, характеризуется четырьмя кардинальными точками и соответствующими им четырьмя кардинальными плоскостями. Это так называемые фокальные и главные точки и фокальные и главные плоскости.

Третье направление - это направление Гамильтона, о работах которого и о развитой им аналогии между геометрической оптикой и механикой мы уже коротко говорили. Основную роль в расчётах Гамильтона играет "характеристическая функция"

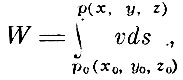
для которой справедливо дифференциальное уравнение в частных производных

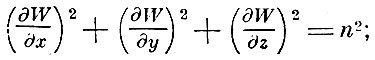
n = n (х, y, z) - заданный показатель преломления. В дальнейшем, по предложению астронома Брунса, функция W получила название "Эйконала", а уравнение для неё - "уравнение эйконала". Как мы уже отмечали, идеи Гамильтона развития не получили.

Геометрическая лучевая оптика - это ньютоновская оптика. Между тем уже в этот период выяснилось (о чём мы скажем ниже) недостаточность чисто лучевых представлений для понимания действия оптических приборов. В рассматриваемый период возникла и бурно развивалась новая математическая схема: волновая кинематика Юнга - Френеля. Основной геометрический образ этой схемы - волновая поверхность, основной аналитический образ - волновое уравнение, исходный принцип - принцип Гюйгенса - Френеля.

Основная проблема для изотропной среды может быть сформулирована так: дано распределение источников и соответствующие граничные условия (диафрагма, экраны и т. д.), найти волновое движение в заданной точке пространства. Принцип Гюйгенса - Френеля позволяет заменить распределение источников некоторой граничной поверхностью, волновое состояние точек которых задаётся.

Впоследствии Кирхгоф показал, что одного задания волновой функции, как это было сделано в первоначальной теории Френеля, недостаточно для однозначного решения задачи. Надо задать ещё скорость изменения этой функции во всех точках поверхности и её нормальные производные. В этом случае ликвидируются такие недочёты гюйгенсовского принципа, как неправильная фаза и невозможность объяснения отсутствия обратной волны.

Тем не менее в руках математиков XIX в. и несовершенный принцип Гюйгенса - Френеля дал замечательные результаты. В разработке математических проблем волновой оптики большую роль сыграли такие работы, как "Дифракционные явления" Шверда (1835), "Колебательная теория света" Кнохенхауера (1839) и особенно исследования Эри и Стокса.

В общем виде проблема представляла непреодолимые математические трудности, поэтому разбирались частные задачи - задачи, относящиеся к типу явлений Фраунгофера. Рассматривалась дифракция от края экрана, прямоугольного отверстия, щели. Относящиеся сюда интегралы Френеля дискутировались и вычислялись в работах Кнохенхауера, Коши, Гильберта и других. Теорию круглого отверстия, которая приводит к бесселевым функциям, разрабатывали Эри, Шверд, Кнохенхауер, в дальнейшем Ламмель, Струве и другие.

Существенную помощь при решении дифракционных задач оказывал принцип, найденный в 1837 г. Бабине. Принцип этот выражает следующее. Представим себе, что волна перехватывается на своём пути экраном, открывающим только часть Е её поверхности. Пусть далее имеются два экрана с отверстиями, с общей площадью соответственно Е₁ и Е₂, так

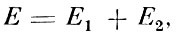
причём экраны располагаются так, что отверстие одного приходится против сплошной части другого. Такие экраны называются дополнительными. Тогда, если х - колебание, возбуждаемое в какой-либо точке Р пространства при наличии одного экрана Е, а х₁ - колебание, возбуждённое в той же точке при наличии одного экрана Е₁, и х₂ - колебание при наличии экрана Е₂, то по принципу Бабине

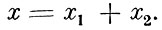
Если, в частности, экран сплошной (Е = 0), что практически имеет место, если точка Р находится глубоко в геометрической тени экрана с малым отверстием, то для дополнительных экранов

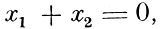
а, следовательно, интенсивность одинакова. Таким образом, распределение света в точках, достаточно удалённых от центра, для круглого отверстия и равного ему круглого экрана будут одинаковы.

Изучение дифракции от отверстий дало возможность глубже вникнуть в действия оптических приборов и в частности разобрать факт, с которым уже столкнулись практики. Так, В. Гершель уже в 1805 г. опубликовал сделанное им раньше наблюдение, что в телескопе получается не точечное изображение звезды, а в виде диска, причём радиус этого кружка уменьшается с увеличением отверстия объектива, а сам кружок окаймлён радужными кольцами. Фраунгофер подтвердил это наблюдение и установил в 1823 г. закон обратной пропорциональности радиуса кружка от радиуса отверстия прибора и от цвета лучей, используемых для освещения. Таким образом, дифракция определяет такое качество оптических приборов, как их разрешающая способность, т. е. способность различать детали рассматриваемого объекта. Термин "разрешающая способность" и её оценка наименьшим углом, при котором ещё разделяются два близких объекта, был введён Дауэсом, который в 1856 г. исследовал телескопы. Классические исследования разрешающей способности зрительных труб провёл в 1858 г. Фуко. Фуко рассматривал в трубы различных диаметров и с разных расстояний листы бумаги с чёрными полосами и установил, что для каждой трубы имеется наименьший разрешающий угол а, не зависящий от её увеличения и обратно пропорциональный диаметру объектива. Формула зависимости для а, найденная экспериментально Дауэсом и Фуко,хорошо подтверждает теорию дифракции от отверстия.

Любопытной иллюстрацией роли практики в научном прогрессе служат эти факты. В астрономических приборах и зрительных трубах вопрос о разрешающей способности и её причинах был поставлен уже в первой половине XIX в, в то время как теория микроскопа дожидалась Аббе и Гельмгольца.

Кинематическая волновая оптика с успехом применялась и в кристаллооптике. Мы уже отмечали такой выдающийся результат, как открытие конической рефракции. Это открытие стало возможным в результате глубокого изучения Гамильтоном формы френелевской волновой поверхности в двуосных кристаллах. Как оказалось, эта поверхность представляет собой частный случай, найденный в 90-х годах Куммером, поверхности 4-го порядка с 16 двойными точками и с таким же числом двойных плоскостей. Математики научились рассчитывать тонкие явления физической оптики.

Но эти успехи не могли удовлетворить физика. Чисто геометрическая схема не давала возможности определить тех количественных и качественных изменений, которые претерпевает световой поток, распространяясь в среде. Необходимо было дать динамическую теорию света. Базой для такой теории послужили результаты, достигнутые теорией упругости, на которых мы должны вкратце остановиться.

Основной закон теории упругости (ut tensio. sicvis - какое натяжение, такая сила) был найден в 1675 г. Гуном. Деятели XVIII в.: Эйлер, Бернулли, Кулон изучали упругие деформации стержней, деформацию изгиба, кручение. Юнг в 1807 г. определял экспериментально модуль упругости (коэффициент в законе Гука) для различных тел, вследствие чего этот коэффициент получил название "модуль Юнга;". Юнг нашёл, что, кроме деформаций, растяжения и сжатия в твёрдых телах, может быть деформация, названная им "сдвигом". Дальнейшие исследования упругости принадлежат Пуассону, Грину и особенно Навье (1785-1833) и Коши (1789-1836)^*.

^* (В дальнейшем экспериментальное исследование упругих констант составляет заслугу Вертгейма (его исследования продолжались с 1844 по 1860 г.); Сен-Велан (1797-1886) изучал изгиб. Теоретические систематические обзоры даны Ламе ("Лекции по теории упругости", 1852 г.), Клебшем ("Теория упругости твёрдых тел", 1862 г.), Веером ("Введение в математическую теорию упругости", 1869 г.).)

Навье в 1821 г. вывел дифференциальные уравнения теории упругости для изотропной упругой среды. Однако уточнение основных понятий и математическое описание динамики упругой изотропной среды было дано в 1822 г. Коши и в 1827 г. было распространено им на случай анизотропной среды.

Коши дал обобщённую форму закона Гука. Упругая деформация в данном элементе объёма упругой среды, характеризуется в данной точке и в данной системе координат шестью функциями, которые на современном языке являются составляющими тензора деформации (Е_xx, Е_yy, Е_zz, Е_xy, Е_хz, Е_yz) и которые составляются из частных производных смещения по координатам. В свою очередь силы натяжения, приложенные к границам выделенного объёма, также определяются шестью величинами, шестью составляющими тензора натяжения. Каждая из этих составляющих является линейной функцией составляющей деформации - в этом заключается обобщённая форма закона Гука, данная Коши. При выводе своих уравнений и Навье и Коши руководились молекулярными представлениями, однако в окончательных формулах среда рассматривалась сплошной, непрерывной.

Вот эти-то уравнения и следствия из них для идеально упругой среды и послужили исходным пунктом в построениях динамической теории эфира^*.

^* (Ламе в своих "Лекциях" так говорит о роли теории эфира в физике: "Существование некоторой эфирножидкой среды неоспоримо доказано... Если эта жидкость и не является единственным источником всех наблюдаемых явлений, то она по меньшей мере должна их видоизменять, способствовать их передаче и осложнять их законы. Вез допущения этого агента, присутствие которого неизбежно, невозможно достичь полного и рационального объяснения природы. Нет сомнения, что такое допущение, умело проведённое, позволит открыть тайну или истинную причину тех эффектов, которые приписываются теплоте, электричеству, магнетизму, всеобщему тяготению, сцеплению, химическим силам...". Свет Ламе уже считает объясненным.)

Первоначальная теория Френеля исходила из представления об абсолютно несжимаемом упругом эфире, в котором выполняется принцип живых сил. Упругость эфира в различных веществах одна и та же, но плотность различна. Переход от одной среды к другой совершается скачком, плотность меняется на конечную величину, на геометрической границе соприкасающихся сред. Предполагая колебания, параллельные поверхности раздела, непрерывными, Френель, как мы видели, нашел выражения для амплитуд отражённой и преломлённой волн, которые были обобщены им и на случай полного отражения.

Предпосылки теории Френеля казались сомнительными. Теория упругости решительно не допускала возможности такого резкого перехода из одной среды в другую. Кроме того, отсутствие продольных волн, по крайней мере на границе, было несовместимо со свойствами механической упругой среды. Коши в ряде работ (1839, 1840, 1849) рассматривал эфир с вкрапленными в него молекулами и получил приведённую нами выше дисперсионную формулу.

Рассматривая пограничные условия, Коши отверг возможность скачкообразного перехода и допустил наличие переходного слоя, в котором колебания и их скорости меняются быстро, но непрерывно. Для случая колебаний, параллельных плоскости раздела, он получил формулу синусов Френеля. В случае колебаний, перпендикулярных плоскости раздела, Коши допустил существование волн сжатия, амплитуда которых убывает очень быстро с расстоянием от границы. Подлеченная им формула отличается от формулы тангенсов Френеля и находится в худшем согласии е опытом, хотя, с другой стороны, исследования Жамена приводили к выводу о наличии переходного слоя.

Грин в 1837 г. разработал в соответствии с принципами теории упругости динамическую теорию эфира, построив модель эфира, состоящего из центров, взаимодействующих с силами, зависящими от расстояния, причём радиус действия сил исчезающе мал по сравнению с длиной волн. Упругие силы, действующие в такой среде, зависят от двух констант: сжимаемости А и твёрдости (т. е. упругого сдвига) В. Грин предполагает, так же как и Френель, что упругость одинакова во всех средах. В случае колебаний, происходящих в плоскости падения, возникают наряду с поперечными волнами сдвига и продольные волны сжатия. Однако Грин предполагает, что скорость этих последних по сравнению со скоростью поперечных волн бесконечно велика. Грин получил формулу синусов, а для случая колебаний в плоскости падения получил формулу, которая только в первом приближении, при не слишком большой преломляемости, переходит в формулу тангенсов Френеля.

Ф. Нейман отказался от принципа равенства упругостей (1835-1842) и выдвинул гипотезу равенства плотностей эфира в обеих средах. В этих предположениях ты была получена формула Френеля для отражённой волны, с тем отличием, однако, что плоскость поляризации Френеля является у Неймана плоскостью колебаний, и формула синусов получается у Неймана для компонент, параллельных плоскости падения, а формула тангенсов - для компонент, перпендикулярных плоскости падения. В связи с этим возникла длительная дискуссия по вопросу о том, какая плоскость является плоскостью поляризации, т. е. плоскостью, в которой нет колебаний линейно-поляризованного света.

К тем же результатам, что и теория Неймана, приводит замечательная теория Мак-Келлога, развитая им в 1839 г. В этой теории Мак-Келлог резко порывает со всеми установившимися традициями в трактовке упругой среды и в частности светового эфира. В теории упругости рассматривается, как мы говорили, симметричный тензор деформации, шесть составляющих которого имеют вид

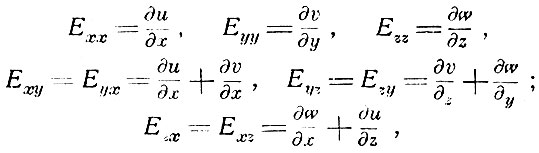
где u, v, w - компоненты смещения точки упругой среды.

Во всех предыдущих теориях (Коши, Грина, Френеля) упругая среда рассматривалась, как среда консервативная, и потенциальная энергия точки явилась однородной квадратной функцией шести составляющих тензора деформации. Составляющие Е_хх, Е_yy, Е_zz определяют деформацию растяжения и сжатия, а Е_xy, Е_yz, Е_zx - сдвиг.

Мак-Келлог предполагает, что единственная деформация упругого эфира, осуществляемая в оптических процессах,- это не сдвиг и не сжатие, а вращение. Компоненты вращения выражаются формулами:

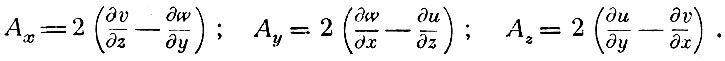
Отсюда Мак-Келлог получает волновые уравнения для компонент смещения, и, как оказалось, из уравнений Мак-Келлога можно получить уравнения, по форме совпадающие с уравнениями Максвелла^*.

^* (Мак-Келлог, как замечает Клейн: "даёт принципиально новые основы френелевской теории,что тем более важно,что,поскольку дело касается математических формул, они совершенно совпадают с электромагнитной теорией света". Это, по выражению Клейна, "своеобразное обстоятельство" - характерный пример диалектического вливания нового содержания в старую форму. То же самое mutatis mutandis можно заметить о выводах Гаусса и Римана, которые, цепляясь за формальный аппарат теории дальнодействия, пришли к выводам, предвосхищающим результаты теории Максвелла (конечная скорость распространения взаимодействия).)

Френелевские законы отражения и преломления вытекают из теории Мак-Келлога, с тем отмеченным уже нами отличием, что френелевская плоскость поляризации совпадает в теории Мак-Келлога с плоскостью колебаний.

Но теория Мак-Келлога не встретила сочувствия, именно в силу необычности своей основной посылки. Представление о среде с непрерывно вращающимися элементами и вместе с тем обеспечивающей процесс передачи поперечных волн с конечной скоростью казалось просто абсурдным. С другой стороны, и построить механическую модель эфира, не допускающую продольных волн и объясняющую громадную скорость света, также оказалось невозможным без допущения противоречия. Грин, как мы видели, должен был сделать предположение о бесконечной скорости волн сжатия, т. е. о бесконечно большом модуле сжатия эфира. Эфир должен был быть более несжимаемым и твёрдым, чем закалённая сталь. Это предположение трудно совместить с крайне сильной разреженностью эфира, которая проявляется в полном отсутствии сопротивления движению планет в эфире. Делались предположения, что, наоборот, эфир абсолютно сжимаем, так что скорость распространения продольных волн равняется нулю.

Но и это представление приводит к противоречиям, так как скорость упругих волн зависит не только от модуля сжатия, но и от модуля сдвига, и, для того чтобы она равнялась нулю, следует допустить отрицательный модуль сжатия, что обусловливает, в конечном счёте, неустойчивость модели. Стоке считал возможным совместить гриновское представление об абсолютной твёрдости эфира с той несопротивляемостью движениям планет, которая более подходит идеальной жидкости. Эфир текуч для мед-ленных деформаций и твёрд для быстрых, наподобие сапожного вара. Всё это ярко характеризует затруднения механистической теории светового эфира , которые ещё более возрастают в теории двойного преломления. Динамические предпосылки френелевской теории не соответствуют механической теории анизотропной среды, развитой Грином и Коши.

Теория Мак-Келлога (и Неймана) приводит к формулам, подтверждаемым на опыте с такой же точностью, как и формула Френеля, с отличием, конечно, в отношении плоскости поляризации. Но сам Мак-Келлог справедливо отмечает, что "если потребовать подтвердить какими-либо аргументами гипотезы, на которых основывается предыдущая теория, то мы окажемся не в состоянии дать удовлетворительный ответ. Мы должны сознаться, что, за исключением закона живых сил, эти гипотезы - только удачные догадки".

Таким образом, можно констатировать, что динамической теории эфира, основы которой были бы свободны от возражений, в рассматриваемый период создать не удалось, хотя волновая кинематика описывала* факты вполне удовлетворительно. В связи с этим Релей в конце XIX в. писал: "Если настоящее положение теории двойного лучепреломления всё же не совсем удовлетворительно, то надо иметь в виду, что эта неопределённость не затрагивает общего принципа.

Почти всякая форма волновой теории, допускающая поперечные колебания, сможет объяснить основное явление, а именно раздвоение луча. Можно с уверенностью предсказать, что когда обыкновенное преломление будет хорошо понято, то двойное преломление не представит больших трудностей".

Итак, ещё не был понят механизм обыкновенного преломления, а перед теорией света вставали задачи объяснения дисперсии, флюоресценции, фосфоресценции, фотохимии. Разгадать эти явления можно было бы, только поняв связь эфира с весомой материей. И эфир, и атомы весомой материи оказались обладающими более сложными и гибкими свойствами, чем думали в XVII в.

В материи (включая и материю эфира) разыгрываются разнообразные процессы, подчиняющиеся закону сохранения и превращения энергии. Какова же эта материя?