Кинетическая теория газов

Но не эти спекуляции отразили новые сдвиги в физическом учении о материи и движении. Физика пошла не по пути, намеченном немецкой идеалистической философией, а по пути Ломоносова, развивая до предельных возможностей программу механистического мировоззрения. Механическая теория тепла и кинетическая теория материи явились продуктом этих усилий.

3 октября 1848 г. на собрании Манчестерского философского общества Джоуль выступил с докладом "Некоторые замечания о теплоте и о строении упругих жидкостей". Этот доклад был напечатан в трудах "Общества" в ноябре 1851 г., и ввиду малой распространённости журнала он остался почти не известным на континенте.

В 1856 г. появилась работа Кренига "Очерки теории газов", за которой последовала работа Клаузиуса, вызвавшая новую публикацию доклада Джоуля в "Philosophical Magazine". Вслед за этими работами появились работы Максвелла, новые работы Клаузиуса, Лошмидта и других. Кинетическая теория газов была создана.

В своём докладе Джоуль, основываясь на опытах по определению механического эквивалента тепла, делает вывод, "что теплота и механическая сила обратимы одна в другую, и, следовательно, стало очевидно, что теплота является vis viva (живой силой) весомых частиц, либо некоторым Состоянием притяжения или отталкивания, способным порождать vis viva (живую силу)".

Рассмотрев вкратце эксперименты по определению механического эквивалента тепла и в частности опыты по адиабатическому сжатию и разрежению воздуха, Джоуль заключает, что эти последние опыты "бросают свет на строение упругих жидкостей, так как они показывают, что теплота упругих жидкостей^* представляет собою ту механическую силу, какой они обладают". И далее: "если известно, что температура газа определяет упругую силу, то отсюда следует, что упругая сила, или давление должны представлять собою эффект движения частиц, из которых составляется всякий газ".

^* (Напомним, что в то время газы называли упругими жидкостями.)

Сформулировав основную идею кинетической теории газов, Джоуль (не зная о работах Ломоносова) рассказывает о возможности объяснения закона Бойля-Мариотта, принимая вместе с Дэви гипотезу о колебательном движении частиц. Он, однако, останавливается как на наиболее простой гипотезе Герапата (1821) о прямолинейном движении частиц газа и производит вычисление скорости движения частиц водорода, предполагая, что молекулы газа содержатся в объёме одного кубического фута при давлении 30 дюймов ртутного столба и температуре 60°. Он находит значение скорости v = 6225 ^фут/_сек.. Далее он показывает, что при уменьшении объёма вдвое давление увеличивается также вдвое, указывает, что скорости должны относиться, как корни квадратные из температуры, и что, следовательно, скорость при 0° С должна быть 6055 ^фут/_сек.. Абсолютный нуль температуры должен лежать на 491 F ниже температуры замерзания воды. Принимая, что удельная теплота газа равна сумме живых сил его частиц, Джоуль вычисляет удельные теплоты газов и сравнивает их с экспериментальными данными Деляроша и Берара.

Отмечая расхождение вычислений с опытом, Джоуль всё же полагает, что это расхождение следует отнести за счёт несовершенства эксперимента и выражает надежду, "что исследования, предпринятые В. Реньо для французского правительства, охватят и важную проблему о теплоёмкости тел и что мы можем в скором времени ожидать новой серии определений удельных теплот газа, отличающейся всей той точностью, какой вполне заслуженно прославился этот замечательный исследователь".

Пока же Джоуль советует воздержаться от изменения теоретических основ динамической теории из-за её несоответствия опытным данным. Это - характерный пример утверждающей силы нового принципа энергии.

Крениг в сочинении "Основы теории газов" (1856) также считает установленным, что теплота - род движения. Однако какова форма этого движения -ещё не ясно. Для идеальных газов можно построить модель, в которой молекулы рассматриваются, как упругие шары, движущиеся без взаимодействия равномерно и прямолинейно, и взаимодействующие друг с другом только в момент столкновения. Исходя из этой модели, можно вычислить давление газа. С этой целью Крениг рассматривает параллелепипед с рёбрами х, y, z и объёмом v = xyz, в котором все молекулы движутся с равными скоростями с параллельно рёбрам сосуда.

Крениг считает, что при каждом ударе молекула сообщает стенке импульс mc, поэтому окончательная формула для давления у него имеет вид

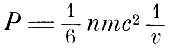
и закон Клапейрона pv = const*nt. Таким образом, температура газа оказывается пропорциональной живой силе молекул газа.

После появления работы Кренига выступил Клаузиус со статьёй "О роде движения, который мы называем теплотой" (1857). Вводные замечания статьи интересны как документ о неизбежном возникновении и руководящей роли гипотезы, несмотря на противодействие формального метода принципов. Клаузиус указывает, что в своих работах о механической теории тепла он, "чтобы исключить возможность какого-либо сомнения в их независимости от особых гипотез, ...прилагал особое старание к тому, чтобы оставить совершенно незатронутым вопрос о роде движения, которое мы воспринимаем в. качестве теплоты".

На самом же деле Клаузиус руководился определёнными гипотезами.

"Однако в действительности мои исследования не были столь свободны от мысли о некоторой гипотезе. Нашему уму свойственна потребность связывать общие понятия с частными представлениями, и потому уже в начале своих работ, относящихся к теплоте, я попытался разобраться во внутреннем состоянии движения нагретого тела и составил себе об этом некоторое представление, которое ещё до первой своей печатной работы о теплоте я применил к различным исследованиям и исчислениям. Это представление было настолько отлично от всего того, что я до сих пор слышал о воззрениях других физиков, что я его считал совершенно новым".

Традиция скрывать при публикации свои пути подхода к задаче, облекать работы в строгую общепринятую форму физики принципов, оказала на этот раз плохую услугу Клаузиусу. Его опередили Джоуль и Крениг. Правда, Клаузиус мог утешиться мыслью, что и Джоуль имел более ранних предшественников, вплоть до Лукреция, причём в исторической справке по неведению отсутствует Ломоносов, однако всё же на новом этапе возрождения кинетических воззрений, на новом круге спирали, Клаузиус мог бы быть и первым. Но, с другой стороны, в своей работе он с большей отчётливостью и ясностью развил основные идеи кинетической теории газов.

Клаузиус исходит из идеи поступательного движения молекул газа: происходящие вследствие этого движения удары молекул о стенки обусловливают давление газа. Однако молекулы могут обладать и внутренним движением, как-то вращение молекул и колебательное движение внутри самих молекул. "Если даже ограничиться рассмотрением только весомых атомов и принять, что последние являются абсолютно неизменными, то все-таки ещё возможно, что молекула, состоящая из нескольких атомов, не образует уже абсолютно неизменной массы, но что отдельные атомы в ней способны двигаться в известных границах и, следовательно, могут колебаться друг относительно друга".

Клаузиус далее делает весьма проницательное допущение, что и в самых простых атомах может быть некоторое количество "более тонкой материи и что последняя, не отделяясь от атома, может поблизости от него совершать некоторые движения". Как мы теперь знаем, движения электронов в оболочке атома действительно имеют место.

Но, каковы бы ни были индивидуальные движения атомов и молекул, в окончательные результаты будут входить статистические средние величины. Это совершенно новая для физики идея, из которой разовьётся в дальнейшем статистическая механика, проводится Клаузиусом со всей отчётливостью. Он показывает прежде всего, что одним из результатов приложения статистических методов .будет положение о постоянном отношении внутренних движений молекул к их поступательному движению, т. е., выражаясь определённее, энергия внутреннего движения составляет определённую долю энергии поступательного движения.

"Это не значит,- указывает Клаузиус,- что указанное определённое отношение между различными движениями наступает у каждой отдельной молекулы и что при дальнейших ударах оно остаётся неизменным: здесь речь идёт лишь о среднем значении, относящемся к очень большому количеству молекул, а именно о среднем значении живых сил движений". Индивидуальные столкновения поэтому могут происходить по различным законам, но когда в результате большого числа столкновений энергия поступательного движения в среднем остаётся неизменной, "то при исследовании совокупного действия большого количества молекул можно пренебречь неправильностями, имеющими место при отдельных столкновениях, и полагать, что по отношению к поступательному движению молекулы следуют общим законам упругости".

Этот статистический подход проводится и в объяснении давления газа. Как каждая молекула взаимодействует с молекулами стенки - дело случая, т. е. результат индивидуального столкновения, определяется настолько сложным переплетением различных условий, что учёт всех причинных связей становится невозможным, и мы называем такой результат случайным. Он, конечно, детерминирован "с необходимостью, присущей и случаю" (Энгельс), но проследить все детали взаимодействий, его определяющих, мы не в состоянии. Но зато результат огромного числа таких случайных взаимодействий со стенкой мы можем предсказать с значительной степенью вероятности, граничащей с достоверностью. "Можно принять, что после отражения молекулы в среднем обладают той же самой живой силой, какую они имели в момент налёта, и что среди отражённых молекул все направления движений по отношению к стенке представлены совершенно так же, как были представлены направления движения налетевших молекул".

Поэтому можно рассматривать, что каждое единичное столкновение совершается по закону упругого удара и что каждая молекула движется с одной и той же, неизменной при данных внешних условиях скоростью (точнее, с средней квадратичной скоростью, равной корню квадратному из среднего квадрата скоростей). Стенка при каждом ударе получает удвоенное количество движения молекул (по направлению нормали к стенке), а не просто количество движения, как полагал Крениг.

"Действие каждого отдельного удара вследствие малой массы молекул очень незначительно, но зато число ударов, приходящихся в течение единицы времени даже на самый малый элемент поверхности, доступный нашему наблюдению, очень велико. Отсюда для нашего восприятия создаётся ложное впечатление, будто стенка получает сообщённое ей количество движения не благодаря отдельным толчкам, а под влиянием постоянно действующей силы, направленной изнутри наружу. Эта сила и есть та самая, которую мы называем давлением".

Нетрудно обосновать пропорциональность давления плотности, если скорость движения молекул не меняется, т. е. закон Бойля - Мариотта. Изменение же скорости сказывается в двояком отношении; во-первых, увеличится число ударов; во-вторых, увеличится интенсивность каждого удара. Поэтому давление должно быть пропорционально квадрату скорости. "Если допустить, что абсолютная температура представляет собой меру живой силы поступательного движения молекул и, следовательно, что она пропорциональна квадрату скорости, то изложенный выше вывод приводит нас к закону Гей-Люссака".

Подсчёт, проведённый Клаузиусом в математических дополнениях к статье, приводит к известному выражению для давления

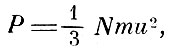
где N - число молекул в единице объёма, m - масса молекулы, u² - средний квадрат скорости движения молекул. Клаузиус устанавливает далее предпосылки, на которых зиждется закон Бойля - Мариотта - Гей-Люссака, т. е. раскрывает кинетическую модель идеального газа. Такая модель должна удовлетворять следующим трём условиям:

1. "Пространство, действительно заполненное молекулами газа, должно быть исчезающе мало по сравнению со всем пространством, занимаемым газом".
2. "Время одного столкновения... должно быть исчезающе мало по сравнению со временем, протекающим между двумя ударами".
3. "Влияние молекулярных сил должно быть исчезающе мало".

При несоблюдении этих условий должны быть отступления от законов идеального газа, и Клаузиус ожидал, что проведённые в 1847 г. исследования Реньо по поведению газов при сильных сжатиях должны дать определённые заключения о собственных объёмах газов. Однако эти ожидания не оправдались, ибо интервал давлений, применяемых Реньо, был недостаточно велик.

Определённые заключения можно было сделать только на основе исследований, относящихся уже к семидесятым годам.

Рассмотрев кинетическую модель газа, Клаузиус останавливается на других агрегатных состояниях и устанавливает, что молекулы находятся в движении во всех трёх состояниях. "При твёрдом состоянии движение происходит таким образом, что молекулы движутся около известных положений равновесия, не оставляя последних окончательно до тех пор, пока на них не воздействуют посторонние силы. Таким образом, у твёрдых тел это движение можно было бы охарактеризовать как колебательное". Клаузиус указывает, что это движение ещё не исчерпывает всей картины, так как могут ещё иметь место интрамолекулярные колебания и вращения молекул около колеблющихся центров тяжести.

"... В жидкости имеет место колебательное, вращательное и поступательное движение, но оно происходит таким образом, что под его влиянием молекулы не разбегаются во все стороны и даже при отсутствии какого-либо внешнего давления остаются в пределах определённого объёма".

Клаузиус, основываясь на своих представлениях, рассматривает далее кинетику испарения. Прежние представления об испарении основывались на допущении сил, действующих равномерно и непрерывно во всей массе жидкости. Клаузиус понимает испарение как статический процесс, основанный на флюктуациях скоростей молекул, "которые претерпевают очень большие изменения наиболее беспорядочным, подверженным случаю образом - от молекулы к молекуле, от момента к моменту - и которые подчиняются только общим законам вероятности".

В жидкостях "молекула при своём движении остаётся в среде притяжения соседних своих молекул или же, если она оставляет последние, то с тем, чтобы попасть в такое же положение по отношению к другим соседним молекулам".

"Однако это верно только для средних величин движения, а так как эти движения совершенно беспорядочны, то можно допустить, что скорости отдельных молекул в очень широких пределах отклоняются в обе стороны от среднего их значения".

В результате таких флюктуации на поверхности жидкости создаются условия, при которых отдельные молекулы выходят из сферы притяжения соседних молекул жидкости, "испаряются". Образовавшиеся молекулы пара, в свою очередь, могут втягиваться внутрь жидкости, и в конце концов устанавливается динамическое равновесие между жидкостью и паром. "Это установившееся состояние равновесия не является состоянием покоя, а таким состоянием, при котором непрерывно происходит испарение и сгущение, причём оба эти процесса протекают с одинаковой интенсивностью и потому взаимно компенсируются".

Ясно, что плотность пара в таком установившемся состоянии будет вполне определённой величиной, определённой числом отрыва молекул от поверхности жидкости в единицу времени, а "это последнее число в свою очередь зависит от интенсивности движения внутри жидкости, т. е. от температуры последней". В том случае, если пространство над жидкостью занято газом, упругость пара, по закону Дальтона, должна остаться той же самой, как и в пустоте. Но этот закон, как справедливо замечает Клаузиус, представляет только описание явления, а не его объяснение. Кинетическое же объяснение явления заключается в том, что и в случае наличия газа над жидкостью его молекулы заполняют очень малую долю пространства над жидкостью и последнее "можно считать пустым и свободно проницаемым для молекул жидкости".

И насыщение пространства молекулами пара происходит "почти что одинаково во всех случаях, независимо от того, занято ли пространство сверх того ещё каким-либо газом или же нет".

Однако иные условия создаются в массе жидкости, условия, которыми определяется процесс кипения. В результате флюктуации в массе жидкости могут образоваться замкнутые пространства, в которые будут испаряться молекулы жидкости,так "что возникшее благодаря этому внутреннее давление пара оказывается в состоянии уравновесить внешнее давление, стремящееся сжать образовавшийся пузырь. Таким образом, давление замкнутого газа должно быть тем больше, чем больше давление, под которым находится жидкость; отсюда становится ясной зависимость температуры кипения от давления".

Таким образом, Клаузиус даёт ясную физическую картину процессов, играющих важную роль в теплотехнике. Эмпирические законы получают прозрачное, наглядное истолкование. Клаузиус рассматривает далее работу газа, расширяющегося под давлением, работу газа в цилиндре с поршнем, и показывает, что эта работа совершается за счёт уменьшения кинетической энергии молекул.

Мы пока не будем останавливаться на других результатах Клаузиуса, имеющих важное значение для атомной теории в химии, мы рассмотрим их несколько позже, когда специально вернёмся к вопросу об атомистике в химии. Здесь остановимся ещё на вопросе о внутренней энергии тел. Внутренняя энергия тел - это энергия движения молекул и атомов и потенциальная энергия их взаимодействия.

Внутренние силы взаимодействия в жидких и твёрдых телах играют большую роль, и потому при расширении таких тел "внешняя работа... обычно бывает незначительной, между тем как внутренняя работа может достичь значительной величины". Иное положение в газах. Здесь "взаимное притяжение молекул... очень незначительно, поэтому, при... удалении их друг от друга производится очень незначительная внутренняя работа; последнее оправдывается тем в большей степени, чем дальше газ находится от своей точки сгущения и чем, следовательно, его состояние больше приближается к состоянию совершенного_* газа, у которого внутреннюю работу, произведенную при расширении, можно считать равной нулю".

^* (Т. е. идеального.)

Для таких газов из первого принципа термодинамики можно получить, что изменение внутренней энергии при нагревании газа при постоянном объёме равно

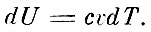
С другой стороны, кинетическая энергия молекул газа

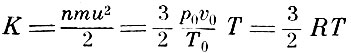
(между прочим, отсюда Клаузиус произвёл подсчёты средних квадратичных скоростей молекул газа при 0° С и нашёл для кислорода u = 461 ^м/_сек, азота 402 ^м/_сек, водорода 1844 ^м/_сек).

Поэтому

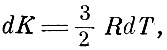
следовательно,

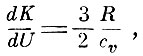
т. е. доля энергии поступательного движения молекул газа составляет определённую постоянную часть всей его внутренней энергии - результат, о котором мы уже говорили выше. Если воспользоваться уравнением Майера R = с_р - c_v,

то

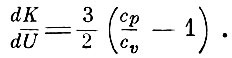
Так, для двуатомных газов 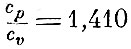и, следовательно,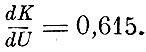

Для одноатомных газов dK = dU, для многоатомных 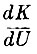будет тем меньше, чем больше атомов в молекуле. Так Клаузиусом были заложены основы классической теории теплоёмкостей газов.

В следующей работе "О средней длине пути молекул газа" (1858) Клаузиус опровергает выставленное против кинетической теории газов возражение, что большие скорости молекул якобы противоречат фактам медленной скорости диффузии, распространения дыма и т. д. Основное понятие, с которым Клаузиус оперирует в этой работе,- это сфера действия молекул. Какова бы ни была природа молекулярных сил, во всяком случае, если отвлечься от сил химического сродства, следует, замечает Клаузиус, "различать две силы, а именно нам придётся допустить, что при сближении двух молекул сначала действует сила притяжения, которая на некотором расстоянии становится уже заметной и затем по мере уменьшения расстояния растёт; но что в тот момент, когда молекулы при-ходят в непосредственное соприкосновение, возникает сила, которая стремится их отдалить друг от друга".

Будет ли эта отталкивательная сила силой контакта упругих твёрдых шаров или она проявляется ещё до контакта, этот вопрос остаётся открытым. "Равным образом, мы оставляем здесь без расследования вопрос о происхождении этих сил, а именно, следует ли обе эти силы приписать самим весовым частицам материи или же одну из них следует приписать некоторому более тонкому веществу, которым, быть может, наделены частицы материи".

Точно так же нет возможности установить - даже в предположении, что точный закон молекулярных сил известен,- что произойдёт при сближении центров молекул до некоторого расстояния х. Будут ли искривлены их пути, или они оттолкнутся,- всё это будет зависеть не только от сил, но и от величин и направления скоростей молекул. Однако можно определить некоторое среднее расстояние σ, такое, что если молекулы проходят на расстоянии, несколько большем σ, то под влиянием взаимного притяжения их пути искривятся, а при расстоянии, меньшем а, они отскакивают друг от друга. "Если под столкновением двух молекул мы будем понимать только последний случай, оставляя без внимания изменения направлений, которые при больших расстояниях вызываются силой притяжения, то... мы можем шар, описанный около центра тяжести молекулы радиусом, равным σ, называть сферой действия молекул".

Простую наглядную модель этого понятия мы получим, если уподобим молекулы упругим шарам. Тогда σ будет диаметром такого шара. Если предположить, что все молекулы неподвижны, кроме одной, центр которой движется со средней квадратичной скоростью u, то для средней длины пути можно легко получить выражение

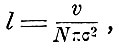
где v - объём, занятый газом, N - число молекул в этом объёме.

В своей работе Клаузиус ввёл другую характеристику для плотности распределения молекул, от которой, очевидно, зависит l. Если предположить, что молекулы размещены в объёме v по кубической системе и обозначить через λ расстояние между центрами молекул, тогда, очевидно,

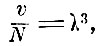
где λ³ - объём ячейки, в которой расположена одна молекула.

Длина свободного пробега

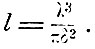
Если же учесть и движение всех молекул, то вероятность столкновений увеличивается, и Клаузиус без вычислений указывает, что вследствие этого длина пробега уменьшится в ³/₄ раза, так что окончательно

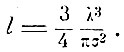
Если ввести радиус молекулы (уподобляя их упругим шарикам) ρ = ^σ/₂, то v' = ⁴/₃Nπρ³ - объём самих молекул газа, а Nλ³ = v - весь объём, занимаемый газом, тогда, очевидно,

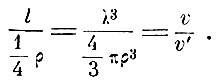
Средняя длина обоюдного пути так относится к четверти радиуса молекулы, как весь объём, занимаемый газом, относится к объёму самих молекул.

В своих расчётах Клаузиус принимал, что все молекулы движутся с одной и той же средней (квадратичной) скоростью. Это допущение - ошибочно. Ошибка была исправлена Максвеллом в его докладе Британской ассоциации 21 сентября 1860 г. Доклад под заглавием "Пояснения к динамической теории газов" был опубликован в "Philosophical Magazine". Этой работой Максвелл заложил новый краеугольный камень в воздвигаемом здании физической статистики и кинетической теории газов.

В то время как философы-идеалисты типа Фехнера (а в дальнейшем Мах, Дюгем, Оствальд и др.) не верили в возможность физического обоснования атомистики и, в частности, определения молекулярных размеров, Максвелл указывал, что хотя в настоящее время нет средств для определения введённой Клаузиусом средней длины пути, знание которой даст возможность определить диаметр молекулы, "однако известные явления, как-то: внутреннее трение газов, прохождение теплоты через газ, а также взаимная диффузия газов, повидимому, указывают на возможность точного определения средней длины пути, проходимого молекулой в промежутке между двумя последовательными столкновениями".

Проницательный взор великого физика увидел в этих разнообразных явлениях общую физическую основу и понял их значение для обоснования новой теории. Впоследствии К. А. Тимирязев, а затем и А. Эйнштейн укажут на значение открытого ещё в 1827 г. ботаником Броуном явления для обоснования принципов молекулярной физики.

Максвелл

В первой своей работе Максвелл разбирает модель,- систему "неопределённого количества малых, твёрдых и совершенно упругих шаров, действующих друг на друга только во время столкновения". Новая физика, таким образом, начинает с наглядных образов и представлений, совершенно в духе Декарта. "Если окажется,- говорит Максвелл,- что свойства подобной системы тел соответствуют свойствам газов, то этим будет создана важная физическая аналогия, которая может привести к более правильному познанию свойств материи".

Любопытно, что эту картезианскую проблему Максвелл и с внешней стороны трактует в духе великих геометров XVII в. Работа построена из "Предложений", разрешаемых, по большей части, геометрическим путём. В первых трёх предложениях речь идёт об определении скоростей сталкивающихся шаров, и в частности в предложении II показывается, что все направления скорости после столкновения равновероятны.

В предложении IV ставится и решается знаменитая задача о распределении скоростей.

Предложение IV. Определить среднее число частиц, скорости которых лежат между заданными пределами, после большого числа столкновений между большим числом одинаковых частиц. И это предложение Максвелл разбирает в геометрическом духе, рассматривая "пространство скоростей", в котором каждая частица, обладающая скоростью v, изображается точкой с координатами х, y, z, где х, y, z - слагающие скорости v. Число частиц, слагающие скорости которых по оси х лежат в пределах от х до х + dx, равно Nf(x)dx; число частиц, слагающие скорости которых по оси y лежат в пределах от y до y + dy, равно Nf(y)dy, и то же имеет место для оси z.

"Но существование скорости х никак не должно влиять на существование скоростей y или z, так как все они находятся под прямыми углами друг к другу и не зависят друг от друга", постулирует Максвелл, и этот далеко не очевидный постулат вызывал сомнения и в правильности самого вывода.

Но в дальнейшем было улучшено и доказательство (Больцман), и закон Максвелла получил многочисленные экспериментальные подтверждения.

Для своей функции распределения Максвелл находит функциональное уравнение

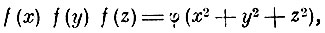
которое удовлетворяется, если положить

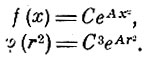
Введя А = - ¹/_α² и имея в виду, что

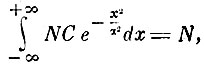
находим

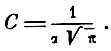
Таким образом: 1) число частиц, компоненты скорости которых по определённому направлению лежат в пределах от х до х + dx, равно

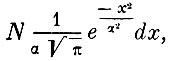
а число частиц, скорости которых лежат между v и v + dv, равно

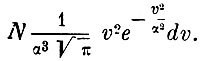
Это и есть знаменитый закон распределения Максвелла. Таким образом, после большого числа столкновений скорости шаров распределяются между ними так же, как по закону Гаусса распределяются случайные, независимые ошибки измерения. Существует, следовательно, наивероятнейшая, наиболее часто встречающаяся скорость молекул, около которой и группируются по преимуществу все остальные скорости, так что скорости много большие или много меньшие вероятной встречаются очень редко.

Эта вероятная скорость и есть постоянная α. Средняя скорость и средний квадрат скорости связаны с α соотношениями:

• средняя скорость
  
  
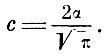
• средний квадрат
  
  

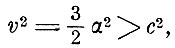
В предложении VI Максвелл доказывает, что в случае двух систем частиц, движущихся в одном и том же сосуде, средняя живая сила каждой частицы одинакова в обеих системах. Это очень важное предложение, из которого, в частности, вытекает закон Авогадро. Столкновения выравнивают кинетические энергии частиц.

В дальнейших предложениях Максвелл решает задачу о средней длине пробега и показывает, что с учётом распределения скоростей она будет выражаться не по Клаузиусу

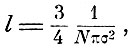
где N - число молекул в единице объёма, σ - радиус сферы действия, а несколько иным выражением

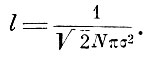
В предложении XII Максвелл даёт новый способ подсчёта давления газов, учитывая взаимные столкновения молекул, характеризуемые длиной свободного пробега I. Результат подсчёта приводит к формуле Клаузиуса

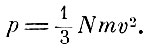
Давление не зависит от длины свободного пути.

В предложении XIII Максвелл рассматривает внутреннее трение газов, механизм которого, по кинетической теории, заключается в переносе количеств движения при различной скорости течения слоев газа.

Отсюда Максвелл находит величину коэффициента внутреннего трения равной

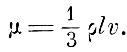
Но, так как длина свободного пробега l обратно пропорциональна плотности р, то мы приходим к "замечательному выводу, что если изложенное здесь истолкование трения правильно, то коэффициент трения не зависит от плотности".

"Этот вывод из математической теории,- продолжает Максвелл,- является крайне поразительным, и единственный опыт, с которым я встретился в этой области, как будто не подтверждает его". Забегая вперёд, скажем здесь, что опыт подтверждает вывод теории в тех областях температур и давлений, к каким вообще применимы выводы классической статистики.

Максвелл же в этой работе считает необходимым "сопоставить свою теорию с тем, что известно о диффузии газов и о прохождении теплоты через газ". Этой задаче посвящена вторая часть работы. Интересно, что если в первой части Максвелл поправлял Клаузиуса, то выводы Максвелла о диффузии и теплопроводности были поправлены и уточнены Клаузиусом. Эти поправки касались более полного учёта условий, имеющих место в различных слоях рассматриваемого газа, и не затрагивали принципа, согласно которому все эти так называемые "явления переноса" обусловлены тепловым движением молекул.

В связи с этим экспериментальное исследование указанных явлений весьма важно для теории. Как обстояло дело в этом отношении в рассматриваемый период?

Явления диффузии и осмоса жидкостей привлекали большое внимание физиков и химиков. Особенно важны были исследования Грэхэма, который пришёл к выводу о существовании двух классов растворов: кристаллоидов и коллоидов, причём эти растворы всегда могут быть разделены из-за различной скорости диффузии, Грэхэм (1834, 1846) исследовал и диффузию газов. Он установил следующий закон: "Скорость диффузии газов через пористую перегородку пропорциональна давлению, под которым газы находятся, и обратно пропорциональна корню квадратному из их плотностей".

Внутреннее трение газов Грэхэм изучал в 1846 и 1849 гг. по методу, предложенному Пуайзейлем в 1840 г. для изучения внутреннего трения жидкости. Этот метод заключался в измерении скорости истечения по капиллярным трубкам. Максвелл и почти одновременно с ним Майер в 1866 г. исследовали внутреннее трение газов по методу, предложенному в 1803 г. Кулоном.

Изучались крутильные колебания горизонтального диска, затухание которых обуславливалось в значительной степени внутренним трением. Эти опыты привели Максвелла к выводу, что внутреннее трение не зависит от давления. Вместе с тем представлялась возможность, зная коэффициент внутреннего трения и плотность газа, определить длину свободного пробега.

Таким образом, началось вторжение в молекулярный мир, и уже в 1865 г. Лошмидт предпринял попытку определения числа и размеров молекул.

Величину, 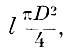где D - диаметр молекулы, а l - длина свободного пробега, можно назвать молекулярным объёмом пути. Если заменить

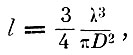
то молекулярный объём пути всех молекул

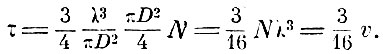
Таким образом

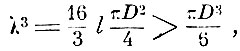
т. е. больше объёма молекулы.

Множитель v, подобранный так, что 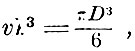Лошмидт назвал множителем сгущения. Очевидно, D = 8vl и, следовательно, зная длину свободного пробега и этот множитель, можно определить диаметр молекулы D. Если предположить, что молекулы в жидком состоянии упакованы плотно, тогда множитель сгущения может быть определён из отношения плотности жидкости к плотности пара. Разумеется, это даст только верхнюю границу для D. Хотя l было определено только для воздуха, который в то время не был обращен в жидкость, однако Лошмидт косвенным путём нашёл

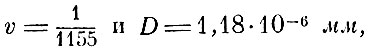
а это давало возможность определить число молекул в единице объёма, которое и стали называть числом Лошмидта.