Электромагнитная масса

Понятие электромагнитной массы было введено в науку Д. Д. Томсоном в 1881 г. В своей книге "Recollections and Reflections" ("Воспоминания и размышления"), вышедшей в 1936 г., он следующим образом поясняет основную идею своей работы.

"Вычисления в этой статье были длинными, но в ней содержится один результат, который может быть получен без вычислений и который образует основу большей части моей работы. По максвелловской теории магнитная сила пропорциональна скорости изменения электрической силы. Если е - заряд и v - скорость, то электрическая сила в данной точке пропорциональна е, а скорость ее изменения пропорциональна ev; следовательно, в любой точке должна существовать магнитная сила, пропорциональная ev; но там, где есть магнитная сила, имеется энергия и величина энергии на единицу объема пропорциональна квадрату магнитной силы. Следовательно, энергия в пространстве вокруг движущегося заряда должна быть равна величине Ae²v², где А - положительная величина, зависящая от формы и размеров заряженного тела. Если частица не заряжена, ее энергия должна быть 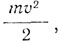, m - масса частицы. Следовательно, полная кинетическая энергия заряженного тела будет (^m/₂ + Ae)v² его кинетическая энергия и, следовательно, его поведение под действием силы будут такими же, как если бы его масса была не m, а m + 2Aе. Следовательно, масса возрастает при заряжении и поскольку это возрастание обусловлено магнитной силой в пространстве вокруг заряда, то приращенная масса находится в этом пространстве, а не в заряженной частице".

Особенно существенное значение имеет тот факт, что электромагнитная масса зависит от скорости. Если для массы электрона, представляющего собой заряженную сферу радиуса а, в состоянии покоя

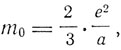
где е - заряд электрона в электромагнитных единицах, а - радиус сферы, то для электрона, движущегося со скоростью v,

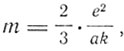
где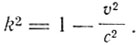

И следовательно,

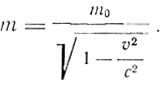
В связи с этим результатом Томсон в своих "Воспоминаниях" пишет: "Максвелл прилагал свою теорию только к среде, свободной от электрических зарядов, но если мы применим ее к случаю движущегося электрического заряда, то мы придем к следствию весьма фундаментального характера, аналогичному тому, которое позже было получено из соображений относительности".

В известном курсе "Теория электричества" немецкий физик Макс Абрагам писал, как бы подтверждая сказанное здесь Томсоном: "У английских исследователей, непосредственно примыкающих к Максвеллу, Д. Д. Томсона и О. Хевисайда впервые встречается представление о такой "кажущейся" массе конвективно движущегося электричества". При этом Абрагам указывает, что он имеет в виду упомянутую выше работу Томсона 1881 г. и работу Хевисайда 1889 г. Сам Абрагам посвятил вопросам динамики электрона и электромагнитной массе фундаментальную работу, опубликованную в "Геттингенских известиях" в 1902 г. и в журнале "Annalen der Physik" в 1903 г. В этих работах Абрагам устанавливает важнейшее понятие электромагнитного импульса и выводит формулу для электромагнитной массы электрона. Исходным пунктом работ являются опыты геттингенского физика В. Кауфмана по отклонению β-лучей в электрическом и магнитном полях, которые Кауфман проводил в течение ряда лет, начиная с 1901 г. Об этих опытах мы подробнее скажем дальше.

Основные постулаты динамики электрона Абрагам сжато и ясно изложил в своей статье "Основные гипотезы электронной теории", опубликованной в 1904 г.

Вот эти постулаты:

• А. В пространстве, лишенном материи и электричества, имеют место уравнения Максвелла.
• В. Электричество состоит из дискретных положительно и отрицательно заряженных частиц, называемых "электронами". В связи с пунктом А Абрагам указывает, что это свободное пространство является абсолютной системой отсчета. В связи с пунктом В он говорит, что электричество является посредником во взаимодействиях материи и эфира.
• С. Всякий электрический ток является конвекционным током движущихся электронов. Конвекционный ток создает такое же магнитное поле, как и эквивалентный ему ток проводимости в теории Максвелла-Герца.
• D. Электромагнитная сила складывается из силы, действующей в электрическом поле на неподвижный заряд, и из силы, действующей в магнитном поле на движущееся электричество.

"Эти четыре положения,- пишет Абрагам,- представляют собой общие положения электронной теории. Всякое исследование, основанное на них, и только такое исследование, будет считаться включенным в рамки электронной теории".

"В моих исследованиях,- пишет Абрагам,- я придал динамике электрона форму, пригодную для истолкования опытов Кауфмана на чисто электромагнитной основе. При этом я, кроме общих основных гипотез электронной теории, ввел следующие частные гипотезы.

• Е. Электромагнитные силы внешнего поля и поля, возбуждающего самим электроном, уравновешиваются в соответствии с механикой твердых тел.
• F. Электрон вообще не может быть деформирован.
• G. Он является шаром с равномерным объемным и поверхностным распределением заряда".

Основываясь на этих гипотезах, Абрагам дает следующие выражения для продольной и поперечной масс электрона, представляющего собой сферу радиуса а и зарядом е, распределенным по ее поверхности.

Продольная масса:

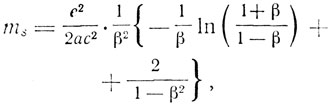
Поперечная масса:

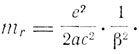
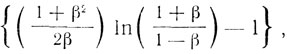
где β = ^v/_c. Для β<<1 величиной β² можно пренебречь, и мы получаем, что для покоящегося электрона продольная и поперечная массы совпадают и равны

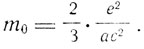
В случае объемного заряда

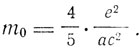
Для обоих случаев общее выражение для продольной и поперечной масс можно написать в виде

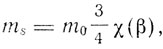
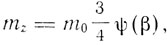
где m₀ подставляется в соответствии с законом распределения заряда (поверхностным или объемным), а функции β имеют вид

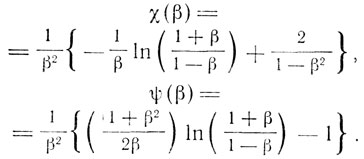
Идея электромагнитного импульса автоматически приводит к существованию светового давления, которое П. Н. Лебедев обнаружил и измерил в своих тонких опытах 1899-1901 гг. Опираясь на эти измерения, австрийский физик Фридрих Газенорль в 1904-1905 гг. получил формулу электромагнитной массы 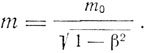В основе его расчетов лежит мысленный эксперимент с полым объемом, заполненным электромагнитным излучением, которому сообщается ускорение. В своем расчете Газенорль приводит к формуле связи между массой и энергией излучения

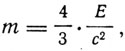
которая отличается от формулы Эйнштейна коэффициентом ⁴/₃.

Ф. Газенорль

Следует отметить, что такую же формулу получил Томсон в 1881 г.

Вернемся, однако, к Лоренцу. Выражения полученные Лоренцом для продольной и поперечной массы

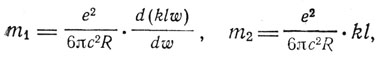
содержат, как и преобразования Лоренца, неопределенную величину i. Преобразуя движение в неподвижном пространстве в движение, отнесенное к движущимся осям, Лоренц приходит к следующим формулам для преобразования ускорений и масс.

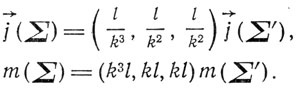
Здесь ∑ обозначает движущуюся систему, ∑' соответствующую неподвижную. Эти соотношения приводят его к результату l = const, и так как для ω = 0, l = 1, то l = 1. "Это ведет к предположению, что влияние поступательного движения (как для отдельного электрона, так и весомого тела в целом) простирается только на размеры в направлении движения, а именно: последние делаются в k раз меньше по сравнению с состоянием покоя".

Из приведенных выше формул для продольной и поперечной масс получаем, положив l = 1,

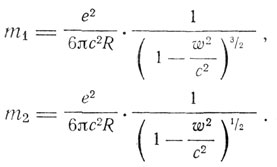
Эти значения, как отмечает Лоренц, отличаются от значений Абрагама. "Результаты Абрагама, касающиеся поперечной массы, подтвердились замечательным образом на измерениях лучей радия в электрическом и магнитном полях, проведенных Кауфманом". Это, отмеченное Лоренцем обстоятельство, вынуждает его поставить вопрос о соответствии его теории с опытами Кауфмана. Он пересчитывает результаты Кауфмана и получает хорошее совпадение со своей теорией.

Вопрос об опытах Кауфмана и его роль в теории относительности был весьма актуальным на ранних этапах теории и поэтому возбудил большую полемику, в которой, кроме Кауфмана, принимали участие Планк и Штарк. К этой полемике и к самим опытам Кауфмана мы вернемся после рассмотрения работы Эйнштейна.

Итак, в теории Лоренца, в отличие от теории Абрагама, электрон является не твердым шариком, а деформируемым образованием. При движении шар сплющивается в эллипсоид. Следует отметить, что подобная деформация шара в эллипсоид при равномерном поступательном движении была рассмотрена в 1889 г. Хевисайдом, показавшим, что при такой деформации равновесное распределение заряда на поверхности остается равномерным, как и в случае неподвижного шара. Мортон и Сир ль в 1896 г. исследовали случай проводящего эллипсоида, движущегося равномерно. Эллипсоид Хевисайда-Лоренца имеет оси (ka, а, а). Бухерер (1904) рассматривал эллипсоид постоянного объема, оси которого равны соответственно а₀k^-2/₃, а₀k^-1/₃, а₀k^-1/₃. Этот эллипсоид единственный, для которого работа сил, вызывающая перемещение, равна приросту электромагнитной энергии. Для электрона Бухерера продольная масса

и поперечная масса

Эту же гипотезу приводил и Ланжевен. 22 сентября 1904 г. Ланжевен выступил на конгрессе в Сен-Луи с докладом "Физика электронов" (доклад Лоренца, составляющий содержание его знаменитой работы, был сделан на заседании Голландской Академии наук 23 апреля 1904 г.). То электрическое и магнитное поле, которое сопровождает движущийся равномерно и прямолинейно электрон, Ланжевен называет электромагнитным "следом" или "бороздой" и, изучая этот след, вычисляет электромагнитную инерцию. Говоря о возможности обнаружить движение электромагнитной системы относительно эфира (абсолютное движение), Ланжевен пишет: "Лармор и более подробно Лоренц доказали, что если в движущейся системе существует только действие, возникшее в результате электромагнитных явлений, то вполне возможно установить точное статическое соответствие (относящееся к положению равновесия или черным полосам интерференции в оптике) между системой, находящейся в движении, и системой, неподвижной относительно эфира. Это может быть, достигнуто при помощи преобразования переменных, которые в электромагнитных уравнениях сохраняют по отношению к движущимся осям такую же форму, какой они обладают по отношению к неподвижной системе осей. Различие этих систем состоит в том, что подвижная из них слегка сплющена по отношению к неподвижной - в направлении движения - на величину, пропорциональную квадрату отношения скорости движения к скорости света.

Это сплющивание в равной мере влияет на все элементы движущейся системы, даже на энергию, если только внутренние воздействия являются исключительно электромагнитными или же ведут себя как таковые и если наблюдатель не может установить это сплющивание, так же как и скорость увлекающего его движения. Так объясняются многочисленные, давшие отрицательный результат опыты в этом направлении Майкельсона и Морли, Рэлея, Брейса, Траутона и Нобеля, если допустить, что все внутренние действия в материи - электромагнитного происхождения. Возможно, что опыты другого типа, чем те, которые пытались производить до сих пор, опыты динамические, а не статические, позволят, наконец, установить абсолютное движение, уловить оси, связанные с эфиром, вместо того чтобы просто предполагать их существование".

Мы привели эту длинную выдержку из Ланжевена потому, что она сжато и ясно рисует ситуацию, обозначившуюся в трудах Лармора и Лоренца. Принцип относительности, оказывается применим только для электромагнитных сил, которые и обусловливают упомянутую деформацию пространства. Если же существуют другие, не электромагнитные силы, то абсолютное движение относительно эфира, возможно, будет обнаружено. При этом опыты должны быть не статического характера, какими они были до сих пор. Деформация системы, описанная выше, относилась к неизменным положениям частиц друг относительно друга. Но частицы (молекулы) находятся в состоянии непрерывного движения.

Лоренц предполагает, что молекулярное движение не изменяет картины и, таким образом, соответствие сохраняется. При этом, конечно, предполагается, что молекулярные силы ведут себя как силы электромагнитные. По поводу этой гипотезы Ланжевен замечает: "При современном состоянии вопроса эта гипотеза слишком сложна и прибегать к ней нет необходимости. Вполне вероятно, что эти постоянные влияния, обеспечивающие устойчивость электрона и представляющие связанную с ним силу тяготения, не сказываются в заметной степени в приведенных выше опытах, и все в них происходит так, как если бы существовали только электромагнитные силы, которые одни лишь играют в них роль".

Таким образом, принцип относительности Лармора-Лоренца-Ланжевена следует назвать электромагнитным принципом относительности, который только приближенно справедлив и для других неэлектромагнитных сил^*.

^* (Правда, Лоренц, выдвинув гипотезу, что и другие силы ведут себя подобно электромагнитным, имел в виду более широкое значение принципа относительности. Но поскольку у Лоренца оставался электромагнитный эфир, его принцип также электромагнитный.)

Говоря об электромагнитной массе, Ланжевен приводит три выражения для отношения ^m/_m0, где m - поперечная масса, которая только к фигурирует в опытах Кауфмана, а m₀ - масса покоя. Это отношение выражается в функции β.

Для изменяющегося сферического электрона (гипотеза Абрагама)

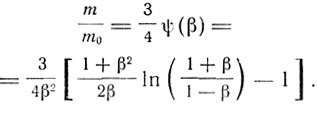
Изменяющийся электрон при постоянном экваториальном диаметре (гипотеза Лоренца)

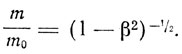
И при постоянном объеме (гипотеза, Ланжевена-Бухерера)

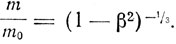
Ланжевен наносит на теоретические кривые вычисленные по этим трем формулам экспериментальные данные Кауфмана и показывает, что совпадение примерно одинаково во всех трех случаях. Опыты Кауфмана, таким образом, не обладают достаточной точностью, чтобы помочь сделать выбор. И тем не менее, отметим это еще раз, они вызвали обширную дискуссию, так как рассматривались как аргумент против-теории относительности.