Модели атомов

Вернемся теперь к теории Бора. Начиная с письма в "Nature", присланного Бором 24 марта 1921г., он усиленно занимается строением электронной оболочки атомов и теорией периодической системы. Но прежде чем перейти к работам Бора, остановимся коротко на моделях атома, предложенных различными авторами в 1918-1922 гг. Следует отметить, что в эти годы развернулась критика представлений Бора о распределении электронов в атомах по кольцам.

Так, А. Смекаль в статье "Замечания к пространственной атомной модели", поступившей в журнал "Zeitschrift fur Physik" 9 марта 1920 г., писал: "Допущение, что электроны окружают "кольцами" положительные ядра, встречается в первых работах по атомной модели Резерфорда-Бора. Несмотря на то что исследования устойчивости Никольсона, Бора и Фёппля не привели к благоприятному результату относительно возможности законченного проведения этого представления, эти сомнения в последующем полностью игнорировались". Смекаль считает, что последующие исследования (работы, о которых он упоминает, были выполнены в 1912-1914 гг.) еще более усилили возражения против теории колец. По его мнению, например, исследования Борна и Ланде сжимаемости кубических кристаллов ясно доказали неосуществимость таких колец в природе. Взамен расположения электронов по кольцам должно быть их пространственное распределение вокруг ядра по некоторым слоям.

В 1916 г. независимо друг от друга В. Коссель и Д. Льюис обратили внимание на "насыщенный" характер конфигурации электронов инертных газов. В этой конфигурации существенную роль играет число 8 - "священное число", как назвал его Зоммерфельд, и этот факт подсказал Льюису статистическую кубическую модель атома.

В 1919 г. Ирвинг Лэнгмюр, используя идеи Льюиса, разработал статистическую теорию пространственного расположения электронов вокруг ядра. Основные положения теории:

1. Электроны в атомах инертных газов располагаются в парных плоскостях, симметрично относительно ядра. Ось симметрии атома перпендикулярна этим плоскостям.
2. Электроны находятся внутри последовательности концентрических слоев, радиусы которых относятся как 1:2:3:4 ...
3. Каждый сферический слой подразделяется на ячейки равновеликого объема. Первый слой (сфера) содержит две ячейки, второй 8, третий 18 и т. д.
4. Внутренние две ячейки могут содержать только по одному электрону каждая, остальные либо по 2, либо по 1 электрону.
5. Электрические и некие специфические атомные силы взаимодействия электронов взаимно уравновешиваются.
6. Если число электронов в слое превышает предельное устойчивое число, то равновесие сил нарушается и электростатические силы отталкивания выбрасывают избыточный электрон в следующий слой.
7. Химические свойства атома обусловлены числом электронов во внешнем слое.
8. Наиболее устойчивыми и симметричными являются конфигурации электронов в благородных газах.
9. Из них наиболее устойчив атом гелия.
10. Весьма устойчивой является система из ядра и 8 электронов, окружающих ядро ("октет"). Расположение электронов в октете может быть двух родов: или по вершинам куба, или по два в вершинах правильного тетраэдра.
11. В атомах всех элементов, кроме, благородных газов, внешние электроны не образуют полного октета и могут вступать в химические соединения между собой, причем электроны из одного атома переходят в другой для образования полного октета.
12. Ни один из электронов не может участвовать более чем в двух октетах.

Здесь весьма интересна идея о ячейках, содержащих электроны в количестве, не превышающем двух. Эту идею следует рассматривать как предшественницу принципа Паули.

Модель Лэнгмюра статическая, хотя он говорит об электростатических и каких-то электродинамических силах, действующих между электронами и электронами и ядром.

Борн и Ландев 1918 г. также пришли к кубической модели. В ряде работ 1919-1920 гг. Ланде пытался развить динамическую модель кубического атома: он искал орбиты, обегающие восемь углов куба, по которым могли бы двигаться восемь электронов, взаимно отталкиваясь и сохраняя кубическую симмертию.

Говоря о пространственных моделях атомов в своем докладе 8 октября 1921 г., Бор писал: "Последовательное применение теории квантов к ядерному атому не давало, однако, возможности до сих пор удовлетворительно ответить на вопрос о глубоких причинах большей устойчивости некоторых электронных расположений в сравнении с другими. С некоторого времени стало ясным, что решение этой задачи нужно искать в возможности пространственного распределения электронных орбит в атоме; недостаточно ограничиваться рассмотрением только таких конфигураций, где все электроны определенной группы атома движутся в одной плоскости, как это принималось для простоты в первых работах о строении атомов. Необходимость в пространственном расположении электронов отмечена с различных сторон. Борн и Ланде в связи с исследованиями о строении кристаллов привели аргументы в пользу пространственной конфигурации; Ланде разработал этот вопрос дальше и предложил различные, так называемые "пространственные модели", в которых электроны в группах атома в каждый данный момент занимают один относительно другого положения с симметрией, подобной симметрии правильного многогранника. Эти модели являются в некотором отношении существенным шагом вперед, хотя и не дают ничего решающего для понимания устойчивости атомной структуры".

Таким образом, аргументы, развитые в пользу пространственной модели, по-видимому, сыграли свою роль. Теперь Бор уже безоговорочно считает, что решение проблемы устойчивости некоторых электронных групп может быть достигнуто только путем анализа пространственных конфигураций электронов. Кубическую модель Льюиса для восьми электронов Бор отвергает, поскольку статические конфигурации "невозможны, если внутриатомные силы чисто электрического происхождения".

"Поэтому Лэнгмюр ... полагает, что природа сил, обусловливающих строение и устойчивость атомов, неизвестна. Он представляет себе в атоме некоторую "клеточную структуру", причем каждому электрону в атоме заранее предназначено место в этой структуре; клетки облегают одна другую слоями таким образом, что число слоев, если считать от ядра наружу, равно числу элементов в периоде в направлении возрастающего атомного номера".

Отмечая, что теория Лэнгмюра была встречена с большим интересом в кругах химиков, Бор все же полагает, что ее постулаты построены специально для этой модели и поэтому чужды "стремлению истолковать специфические свойства различных элементов на основании общих законов, определяющих взаимодействие частиц любого атома". Как видим, идея специфических атомных сил и принцип Паули еще не созрели, и даже такой мыслитель, как Бор, отнесся к ним скептически. Он в своем изложении даже не упоминает о принципе размещения электронов по ячейкам, сформулированном Лэнгмюром. Рассмотренные выше модели были подсказаны химическими свойствами и периодической системой. Мы рассмотрим теперь модель другого рода, которая опиралась на опыты Франка-Герца. Речь идет о модели Э. Уайтеккера, изложенной им в докладе Королевскому обществу 8 мая 1922 г.

Уайтеккер отправляется от факта, что в столкновениях электронов с атомами наблюдаются в зависимости от энергии электрона случаи упругого или неупругого рассеяния. Он моделирует этот факт представлением о "магнитном токе", циркулирующем в атоме. Грубо такую модель можно представить "магнитным колесом", составленным из полосовых магнитов, одни полюса которых расположены по периферии атома, а другие в центре, наподобие спиц колеса. Электрон, приближаясь по оси колеса к атому, приводит периферийные полюса во вращение, что и реализует магнитный ток. При этом, если скорость электрона будет меньше некоторой предельной, электрон оттолкнется электрическим полем магнитного тока и угловая скорость колеса, приобретаемая при подходе электрона, теряется во время его возвращения назад. Электрон будет сталкиваться с атомом упруго, если его скорость

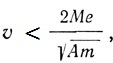
где М - сумма магнитных масс, расположенных на периферии колеса, А - момент инерции колеса (атома), m и e - масса и заряд электрона. Для предельной скорости 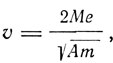угловая скорость вращения колеса определяется соотношением

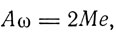
а энергия вращения

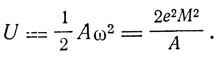
Таким образом, если энергия электрона меньше U, его столкновение с атомом будет упругим; если же больше U, то столкновение будет неупругим, причем атом при пролетании через него электрона отбирает энергию U.

Магнитный ток эквивалентен "электрическому листку" - конденсатору. Этот конденсатор излучает энергию частоты v, причем

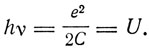
Уайтеккер подчеркивает, что его модель является только моделью, которой можно представлять квантовый механизм поглощения энергии атомом. Его модель обсуждали Бейкер, Г. А. Лоренц, Дж. Элдридж. Лоренц в своей статье, опубликованной в "Докладах Амстердамской академии" в том же, 1922 г., когда Уайтеккер делал свой доклад, получает его результаты, предполагая непрерывное распределение магнитных масс по периферии атома. О модели Уайтеккера он пишет: "Я не должен позабыть сказать, что Уайтеккер не хотел приписывать чересчур большое значение специальному виду своей модели. Он замечал, что после того, как получена удовлетворительная система уравнений, мы можем отбросить модель, посредством которой мы пришли к ней. Что особенно мне кажется интересным в идее Уайтеккера, это то, что она показывает возможность четкого критерия, посредством которого можно заключить, будет ли столкновение эффективным или нет. Такой критерий, конечно, должен быть". Бейкер в том же году рассмотрел более общий случай движения электрона: скорость его может быть направлена не только по оси атома, но и любым образом, лишь бы он проходил через магнитную систему атома. Он получил то же выражение для предельной энергии электрона, что и Уайтеккер.

В 1925 г. модель Уайтеккера обсуждал Элдридж. Он обратил внимание на то, что полюса в центре должны получать момент, противоположный моменту, получаемому периферийными полюсами и, следовательно, полный угловой момент, получаемый системой, должен равняться нулю. Элдридж указал, что модель Уайтеккера должна работать только при униполярном магнетизме, а концепция униполярного магнетизма противопоказана физике. Аллен возразил, что всегда можно подобрать движение электрона так, чтобы он подвергался действию полюсов только одного знака, подобно опыту Фарадея с магнитным вращением.

Спор решила квантовая механика, изгнавшая из физики наглядные модели атома.