Начало новой эпохи в физике

Обратимся теперь к ситуации в квантовой механике после работ Бора-Крамерса-Слэтера. Эта ситуация была очень напряженной и вызывала у тогдашних физиков чув. ство глубокой неудовлетворенности. В. Паули писал 21 мая 1925 г. Кронигу: "Физика теперь снова зашла в тупик, во всяком случае, она для меня слишком трудна, и я предпочел бы быть комиком в кино или кем-нибудь вроде этого и не слышать ничего о физике". Гейзенберг в это время находился на острове Гельголанде, проходя курс лечения. Здесь он занялся проблемой ангармонического осциллятора. Сообщая о своих результатах в письме Кронигу от 5 июня 1925 г., Гейзенберг писал: "В этой схеме мне больше всего нравится то, что все взаимодействия атома с внешним миром на самом деле можно свести к вероятности перехода (отвлекаясь от случаев вырождения). Не нравится мне прежде всего математическая сторона... Физический смысл вышеизложенной схемы вычисления интенсивностей также выглядит весьма странно".

В письме Паули от 24 июня Гейзенберг писал: "Основная аксиома состоит в том, что при вычислении каких-либо величин, например энергии, частоты и т. д., должны использоваться только соотношения между принципиально наблюдаемыми величинами". Эта основная методологическая установка Гейзенберга понравилась Паули, и он поощрил Гейзенберга к дальнейшей работе в этом направлении. 29 июня 1925 г. Гейзенберг представил в редакцию журнала "Zeitschrift fur Physik" статью "О квантовотеоретическом истолковании кинематических и механических соотношений". Аннотация к статье автора гласила: "В работе сделана попытка получить основания для квантовотеоретической механики, базирующейся исключительно на соотношениях между принципиально наблюдаемыми величинами".

Физический семинар в Копенгагене. (В первом ряду: Бор, Гейзенберг, Паули, Гамов, Ландау, Крамерс)

Методологическая установка Гейзенберга не выдержала испытания временем. Принцип введения в теорию только наблюдаемых величин не мог быть плодотворным, и слишком явное махистское происхождение его напоминало о провале похода Маха против "принципиально ненаблюдаемых" атомов и электронов.

Гейзенберг, однако, начинает свою статью с критики старой классической теории, которая вводила такие "принципиально ненаблюдаемые" величины, как положение и период обращения электрона. По мнению Гейзенберга, неудачи старой квантовой теории в области сложных атомов и других проблем объясняются именно этим дефектом теории. "При таком положении вещей,- писал он,- кажется самым лучшим совершенно отказаться от всякой надежды на наблюдение до сих пор не наблюдаемых величин (таких, как положение, период обращения электрона) и, допуская одновременно, что частичное согласие упомянутых квантовых правил с опытом является более или менее случайным, попытаться построить квантовотеоретическую механику, более или менее аналогичную классической механике, в которой встречались бы только соотношения между наблюдаемыми величинами".

Гейзенберг в качестве примера такой теории указывает на теорию дисперсии Ладенбурга-Крамерса, в которой вместо движений электронов в атомной модели рассматривались "виртуальные" эйнштейновские переходы и соответствующие частоты, которые фактически наблюдаются на опыте.

Рассматривая теорию излучения в классической теории, Гейзенберг указывает, что, кроме обычных значений поля в волновой зоне, соответствующих излучению диполя, могут появиться "квадрупольные" члены и члены более высокого порядка относительно скорости электрона. Возникает вопрос, что соответствует высшим приближениям в квантовой теории. Этот вопрос не является электродинамическим, а чисто кинематическим и может быть сформулирован так: пусть вместо классической величины x(t) дана соответствующая квантовотеоретическая величина. Какая квантовотеоретическая величина будет соответствовать x(t)? Прежде всего, Гейзенберг указывает, что в новой квантовой теории вместо таких характеристик электрона, как положение в пространстве, следует сопоставить электрону его излучение, которое описывается частотами и амплитудами. Частоты в квантовой теории являются функциями двух переменных вида

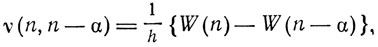
тогда как классические частоты определяются равенством

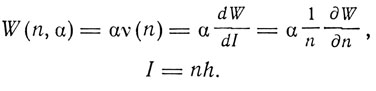
При этом между частотами имеют место комбинационные соотношения:

в классической теории

в квантовой теории

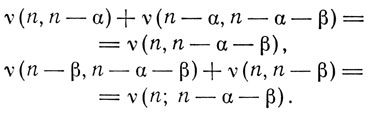
Амплитуды представляются комплексными векторами, определяющими также поляризацию и фазу. Каждый такой вектор является также функцией двух переменных n и α и определяется как действительная часть выражения

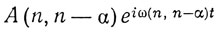
(А - комплексная величина, которую Гейзенберг обозначает готической буквой). В классической теории ей соответствует действительная часть коэффициента Фурье

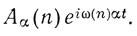
Фаза, входящая в комплексный вектор А(n, n - α), имеет смысл и в квантовой теории, что выясняется из определения величин, соответствующих x(t)2. Если x(t) в классической теории представляется интегралом Фурье

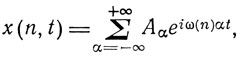
или соответственно

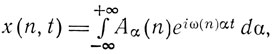
то величине x(t)² в классической теории будет соответствовать выражение:

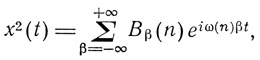
где

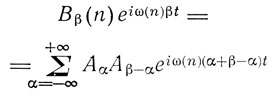
и соответственно аналогичные выражения для случая представления x(t) интегралом Фурье.

Гейзенберг допускает, что в квантовой теории эти соотношения должны быть заменены соотношениями вида

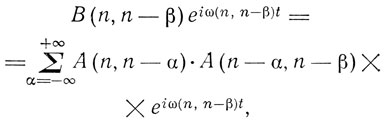
и соответствующими выражениями для случая интеграла Фурье. Постулированная им связь получается почти естественно из комбинационных соотношений. Из этого соотношения вытекает важное физическое значение фазы вектора А в квантовой теории, которая входит в величину В.

Таким же образом можно найти квантовый аналог величины x(t)³ и вообще x(t)ⁿ. Вообще, если дана какая-либо функция f[x(t)], то, если эта функция разложима в ряд по степеням x(t), можно найти ее квантовый аналог. Далее возникает вопрос, что является квантовым аналогом произведения x(t)*y(t)? Пусть x(t) в классической теории представляется посредством векторов A, а y(t) - посредством В.

Тогда произведение x*y представляется векторами С, причем

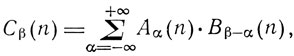
в квантовой теории этому соответствует равенство

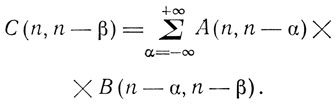
Но если в классической теории x(t)*y(t) = y(t)*x(t), то в квантовой теории этот переместительный закон вообще не имеет места. Выписывая свою "алгебру представителей", Гейзенберг еще не догадывается, что он имеет дело с соотношениями матричного исчисления. На это указал ему М. Борн, разработавший вместе с П. Иорданом математический аппарат новой теории.

После этих кинематических соображений Гейзенберг переходит к атомной механике, задачей которой является определение величин A, v, W (амплитуды и фазы, частоты и энергии системы) из данных сил системы. В существовавшей теории эта задача решалась двумя этапами:

1. Устанавливалось уравнение движения системы
   
   
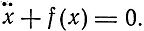
2. Определялись допустимые движения периодического характера с помощью условий
   
   

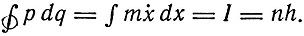
В новой квантовой схеме достаточно ограничиться установлением квантового аналога уравнению движения с помощью указанной выше математической схемы. В общем случае эта задача представляет большие математические трудности. В особенности трудной казалось Гейзенбергу задача водородного атома. Он ограничивается примером ангармонического одномерного осциллятора, уравнение движения которого имеет вид

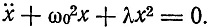
В классической теории это уравнение решается с помощью подстановки

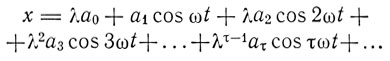
В квантовой теории этому ряду сопоставляется ряд выражений:

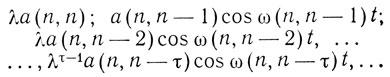
Подстановка в уравнение дает реку-рентные формулы как для классических амплитуд и частот, так и для квантовых. Кроме того, выписываются квантовые условия, которые в классической теории имеют вид

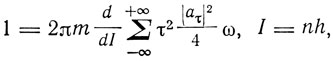
и в квантовой теории Гейзенберга

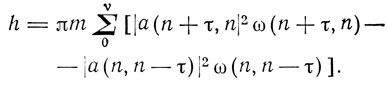
Выражения Гейзенберга приводят к выражению энергии осциллятора

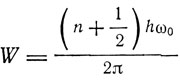
вместо классического

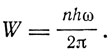
Выражение для энергии W будет точным для гармонического осциллятора и приближенным с точностью до λ² для ангармонического. Для ротатора Гейзенберг получил выражение энергии

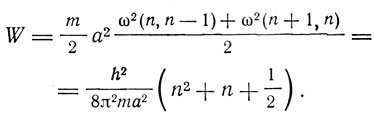
Причем частота

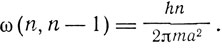
Так что

Формула Гейзенберга для ротатора отличалась от формул, полученных по старой квантовой теории. Гейзен-берг замечает, что опорой новых формул может служить то обстоятельство, что многие полосатые спектры, по Крацеру (1922), как оказывается, требуют именно таких формул, которые старая квантовая теория пыталась объяснить полуцелым квантованием. Таково содержание этой работы Гейзенберга, которую автор заканчивает словами: "Будет ли предложенный здесь метод определения квантово-теоретических данных посредством соотношений между наблюдаемыми величинами уже рассматриваться как вполне удовлетворительный в принципиальном отношении или же этот метод представляет не более как начало наступления на физически, очевидно, весьма сложную проблему квантово-теоретической механики, можно будет узнать только путем более глубокого математического исследования здесь весьма поверхностно использованного метода".

Борн, прочитавший рукопись Гейзенберга, сразу увидел в его правиле умножения "векторов-представителей" правило умножения матриц. Он высоко оценил работу Гейзенберга, отмечая, что в этой работе Гейзенберг "гениальным приемом вызвал новый поворот квантовой теории". 27 сентября 1925 г. Борн и Иордан представили в "Zeitschrift fur Physik" статью, в которой изложены основы матричной механики и ее применение к гармоническому осциллятору. Общую разработку математического аппарата теории они дали в статье, полученной в "Zeitschrift fur Physik" 16 ноября 1925 г. Борн в это время уехал в США, где с 14 ноября 1925 г. по 22 января 1926 г. читал в Массачузетском технологическом институте лекции, составившие содержание вышедшей в 1926 г. книги "Проблемы атомной динамики", первая половина которой была посвящена изложению квантовой механики. Теория Гейзенберга воодушевила Паули, который писал Кронигу 9 октября 1925 г.: "Механика Гейзенберга снова вернула мне радость и надежду. Хотя она и не дает решения загадки, но я верю, что теперь снова можно двигаться вперед. Прежде всего надо освободить механику Гейзенберга от геттиигенской формальной оболочки учености, чтобы лучше раскрыть ее физическое содержание". В свою очередь Паули воодушевил Гейзенберга. В своих воспоминаниях об этой эпохе Гейзенберг писал: "Сам я был тогда несколько удручен тем, что мне никак не удавалось вывести из новой теории простой спектр водорода. Однако уже в октябре того же года Паули преподнес мне сюрприз: законченную квантовую механику атома водорода. Мой ответ от 3 ноября начинался словами: "Едва ли нужно писать, как сильно я радуюсь новой теории атома водорода и насколько велико мое удивление, что Вы смогли так быстро ее разработать".

Но теория атома в новой механике была также разработана почти в то же самое время английским физиком П. А. М. Дираком, выступившим в том же, 1925 г. со своей интерпретацией новой теории. Он развил особую символическую алгебру состояний и наблюдаемых величин. Каждое состояние системы можно обозначать символом ψ, удовлетворяющим принципу суперпозиции, так что состояние А, изображаемое символом ψ₀, может быть получено путем суперпозиции состояний В, изображаемого символом ψ₁ и С, изображаемого символом ψ₂, причем

Когда состояние накладывается само на себя, результирующее состояние совпадает с исходным. Если представить ψ как вектор в пространстве с достаточно большим числом измерений, то состояние вполне определяется направлением вектора. Наряду с символом ψ состояние может быть описано комплексно-сопряженным вектором φ. В своей книге "Принципы квантовой механики", первое издание которой вышло в 1930 г., Дирак так описывает свой метод: "Типичное вычисление в квантовой механике ведется по следующей схеме: дается, что система находится в определенном состоянии, в котором динамические переменные имеют определенные значения. Это условие записывается в виде уравнений между символами, обозначающими состояние и динамические переменные. Из этих уравнений выводятся в согласии с аксиомами нашей символической алгебры новые уравнения, а из них получаются уже и физические следствия. Истинная сущность каждого из употребляемых символов нигде не уточняется и нет никакой необходимости ее знать".

Из приведенного видно, что новая механика и у Дирака, и у Гейзенберга оставалась абстрактной математической схемой, которая приводила к правильным результатам, хотя физический смысл применяемых символов и операций оставался неясным. Гейзенберг назвал период 1925-1927 гг. периодом "прояснения формальных основ". Более наглядную и более привычную для физиков математическую теорию новой механики начал в 1926 г. разрабатывать Э. Шредингер под названием "волновой механики". Таким образом, 1925-й год начинает напряженный и весьма результативный период разработки сначала формальных, а затем физических основ новой квантовой теории.