Масштабы

Кристалл небес мне не преграда боле,
Но вскрывши их,
подъемлюсь в бесконечность.

Джордано Бруно

Мы собрались выйти за пределы Солнечной системы. Что там дальше? "Сфера неподвижных звезд", то самое "седьмое небо" Аристотеля, которое собрался вскрыть бесстрашный Бруно. Но нет ли на этом небе кусочка, который ближе к нам? Проще, какая звезда ближе всех к Солнечной системе? Ответ известен - а Центавра (или Кентавра), Ответ, в общем, правильный, но неточный. Даже в небольшой телескоп видно, что а Центавра - двойная звезда. Кто ближе всех - а Центавра А или а Центавра В? Оказывается, ни А, ни В. На расстоянии 2,2° от пары А и В находится слабая звездочка, которая так и называется - Проксима (Ближайшая). 4,3 года идет до нас свет от а Центавра, а от Проксимы - почти на 14 суток меньше. Оказывается, Проксима не только на небе расположена недалеко от пары АВ, но и в действительности, в пространстве, близка к ним. А раз так, значит (закон-то тяготения - всемирный!), она должна обращаться вокруг них. Так может быть, ей недолго осталось быть Проксимой? Выяснить это нас призывает

Задача 17. Считая, что Проксима движется вокруг а Центавра по круговой орбите, в плоскости которой лежит направление на Солнце, определить, когда Проксима потеряет право на свое название. Масса а Центавра М_АВ = 1,9 M_⊗.

Чья же все-таки задана масса, и вообще, вокруг чего обращается Проксима? Да вокруг АВ. Даже если мы прилетим на Проксиму и увидим А и В на заметном удалении друг от друга, все же по гравитационному действию на таком расстоянии нелегко отличить две звезды от одной, имеющей их суммарную массу.

"Седьмое небо" - наша Галактика, миллиарды и миллиарды звезд. Есть среди них звезды в сотни раз тяжелее Солнца и в десятки раз легче его. Есть звезды, внутри которых легко поместится орбита Земли, и есть такие, которые меньше самой Земли. Но больше всего различаются звезды своей плотностью. Тут и такие, по сравнению с которыми воздух покажется "сверхплотным" веществом, есть и совсем другие. Есть, например, нейтронные звезды. Тяготение "втиснуло" электроны в атомные ядра, получилось, в сущности, одно сверхбольшое ядро. Плотность ядерного вещества можно узнать, вспомнив, что ядро, в котором "лежит" практически вся масса атома, по размеру в сотню тысяч раз меньше своей электронной оболочки. Но наш путь -

Задача 18. Период обращения самого быстрого спутника типичной нейтронной звезды T_н = 10^-3 с. Оценить плотность ядерного вещества.

Если мы еще помним задачи 16, то остается проверить ответ.

Мы посмотрели на несколько звезд нашей Галактики. А теперь попробуем взглянуть на нее в целом. Что мы увидим? Звезды, много звезд, и среди них наше великое, такое незаметное среди других Солнце. Где и как оно живет в Галактике? Некоторое представление об этом дает.

Задача 19. Солнце обращается вокруг центра Галактики за 220 млн лет по орбите радиуса 2 млрд а. е. (около 10 килопарсеков). Подсчет звезд, находящихся к центру Галактики ближе, чем Солнце, дает оценку их суммарной массы M_г⁰ = 10¹¹M_⊗. Оценить "скрытую массу" внутренних по отношению к Солнцу областей Галактики, т. е. массу, которая не поддается учету при оптических наблюдениях.

Конечно, Галактика - не точка и даже не пара близких звезд. Тем не менее мы получим разумную оценку ее массы, если и в этой задаче сосредоточим все вещество в центре Галактики. Более точные расчеты, учитывающие распределение вещества в Галактике у дают несущественно отличающийся результат.

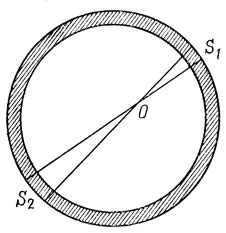
Рис. 5

Здесь, на мой взгляд, стоит отвлечься. Вспомним, почему можно рассматривать лишь те звезды, которые находятся между центром Галактики и орбитой Солнца. Рассмотрим шаровой слой вещества: объем, ограниченный двумя концентрическими сферами очень близких радиусов (рис. 5). Возьмем произвольную точку О в полости, ограниченной этим слоем (его внутренней сферой). Выделим узенькие конусы, имеющие общую вершину в точке О, и общие образующие. В слое вещества они выделяют объемы, пропорциональные квадрату расстояний от точки О до соответствующих участков слоя. Если плотность вещества внутри слоя (между сферами) одинакова на участках S₁ и S₂, притягивающие массы также пропорциональны квадратам расстояний. Нетрудно понять, что на тело, помещенное в точке О, со стороны масс, расположенных в S₁ и S₂, будут действовать равные и противоположно направленные силы. Теперь ясно, что весь такой шаровой слой не создает поля сил тяготения в полости. Значит, при сферически симметричном распределении масс - от слоя к слою плотность может меняться, она должна быть одинаковой только внутри каждого слоя - поле тяготения создают только "внутренние" массы.

Конечно, в Галактике распределение масс далеко от сферически симметричного. Наш расчет остается грубой оценкой. В действительности влияние внешних частей Галактики даже немного ослабляет притяжение к ее центру. С другой стороны, центральные части Галактики притягивают Солнце несколько сильнее, чем при сферически симметричном распределении масс. Учет всех этих деталей привел бы к весьма громоздким выкладкам, не меняя нашей оценки по порядку величины.

Наша Галактика - далеко не вся Вселенная. Долго люди не подозревали, что расплывчатое пятнышко на небе - Туманность Андромеды - самый удаленный объект, видимый невооруженным глазом. Ведь это другая звездная система, подобная нашей, другая галактика. К мутному пятнышку в созвездии Андромеды мы вернемся позже, а сначала посмотрим на самые близкие к нам галактики - так называемые Магеллановы Облака. Их два, Большое и Малое. Они гораздо меньше Туманности Андромеды и нашей Галактики. Но они в десяток раз ближе к нам, поэтому выглядят заметно эффектнее Андромеды. К сожалению, на северном небе они не видны, поэтому узнали о них позже. Конечно, европейцы давно бывали в Южном полушарии, но этих людей больше интересовали пряности и золото, чем небо. И только любознательный спутник Магеллана Пигафетта обратил на них внимание, описал, рассказал о них европейским ученым. До Магеллановых Облаков - 200 тысяч световых лет! Но тяготению и такие расстояния не помеха. Облака обращаются вокруг нашей Галактики, как Луна вокруг Земли, Земля вокруг Солнца, Проксима вокруг а Центавра. Другой вопрос, можно ли это увидеть. Ответ на него дает

Задача 20. Один из крупнейших телескопов в Южном полушарии - телескоп Европейской южной обсерватории в Чили - имеет зеркало диаметром 3,6 м. Какое потребуется время, чтобы, сравнивая полученные на этом телескопе фотоснимки, можно было заметить движение Магеллановых Облаков вокруг Галактики? Суммарную массу Галактики принять равной 2,5×10¹¹M_⊗. Считать, что Магеллановы Облака движутся вокруг Галактики по окружностям.

Возникает законный вопрос - с чем сравнивать по-ложение Магеллановых Облаков? С еще гораздо более удаленными объектами. Ведь в сильный телескоп видны галактики, находящиеся в миллионах и миллиардах световых лет от нас. Их видимое движение не заметить не только за столетия, но и за многие тысячелетия.

Вспомним, к примеру, галактику Туманность Андромеды, или просто Андромеду. До нее два с четвертью миллиона световых лет. Наша Галактика и Андромеда - два главных члена так называемой Местной Группы. В Группе - около 40 галактик, но на две самые большие приходится примерно 90% массы. Поэтому Галактика и Андромеда - самые далекие друг от друга объекты,

движение которых относительно друг друга можно рассматривать, не принимая во внимание тяготение других тел^*. Зато возникает другая трудность. Во всех предыдущих задачах одно из тел было гораздо массивнее другого, и его можно было считать неподвижным центром тяготения. Андромеда же и Галактика имеют близкие массы. Поэтому нельзя сказать, что одна из них обращается вокруг другой. Они обращаются друг вокруг друга, или, вернее, вокруг общего центра масс. О том, как "быстро" это происходит и насколько трудно заметить их относительное движение.

^* (Похоже, что это безответственное заявление успело устареть. Исследования последних лет рисуют такую картину "ближайших" наших окрестностей. Местная Группа входит в Местное Сверхскопление, центральная часть которого находится в шестидесяти миллионах световых лет от нас в направлении созвездия Дева. Можно говорить о притяжении Местной Группы к Деве, о движении Местной Группы вокруг компактной группировки из тысячи галактик - центра Местного Сверхскопления, Сверхскопления Дева. Более того, и Дева, и соседи (удаленные на двести мил-лионов световых лет сверхскопления Гидра - Центавр и Павлин - Индеец), похоже, движутся в одном направлении под действием неправдоподобно массивного притягивающего центра. Это Суперсверхскопление несколько десятков тысяч галактик - расположено где-то между Скорпионом и Хамелеоном на расстоянии около пятисот миллионов световых лет. Ему придумано устрашающее название - Великий Аттрактор (attractio - "притяжение"). Из обилия оговорок ясно, что приведены, как говорится, непроверенные данные. Несколько групп ученых работают над их уточнением.)

Задача 21. Рассмотреть вопрос задачи 20 применительно к Туманности Андромеды, наблюдаемой с помощью БТА. Масса Андромеды M_А=3,6×10¹¹M_⊗.

Расстояние до Андромеды только что названо, масса Галактики упоминалась в предыдущей задаче, диаметр объектива БТА, как мы помним,- 6 м; будем также считать, что наблюдение ведется на длине волны 6×10^-7 м.

Осталось вспомнить, как Ньютон обобщил третий закон Кеплера. Ньютон рассмотрел общий случай движения двух тел вокруг центра масс. Он нашел, что в любой паре одно и то же значение имеет следующее соотношение (М+m)Т²/а³, где М и m - массы взаимодействующих тел, Т - период обращения вокруг центра масс, а - максимальное расстояние между телами - большая полуось эллипса, который одно тело описывает относительно другого.

Мы не знаем, по каким траекториям движутся Галактика и Андромеда. Остается надеяться, что мы не сильно ошибемся, ??/ш предположим, что они движутся по окружностям.

А для этого случая мы сами вполне можем получить обобщенный третий закон Кеплера. Посмотрим на рис. 6. Тело, например М, движется под действием силы GMm/(R+r)² по окружности радиуса г. Его ускорение - 4π²r²/Т²r. Для. нахождения r используем два соотношения. Во-первых, r+R=a; во- вторых, по правилу рычага Mr=mR. Решая полученную систему уравнений, находим, что (m+М)Т²/а³=4π²/G. Используя непосредственно полученную формулу или сравнивая движение Галактики и Андромеды с движением Земли вокруг Солнца, находим, что период обращения галактик составляет почти 70 миллиардов лет. Как мы выяснили в задаче 6, Андромеда должна пройти 10^-7 радиана, т. е. надо прождать 1,6×10^-8 оборота, а это больше 1000 лет.

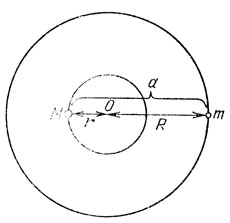
Рис. 6

Но давайте двинемся по шкале масштабов в обратную сторону. Вернемся в нашу Галактику - в ней тоже нередко встречаются двойные системы.

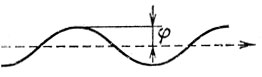
Рис. 7

Так, в 1844 году выдающийся математик и астроном Рис. 7 Бессель обнаружил, что самая яркая звезда нашего неба Сириус движется не по прямой, а примерно по синусоиде (рис. 7). Максимальное угловое отклонение Сириуса от прямолинейного пути φ=2,3". Период "колебаний" Т=50 лет. Бессель предположил, что у Сириуса есть спутник - невидимая звезда Сириус В ("главную" звезду стали называть Сириус А). Через 18 лет отец и сын Кларки, прославленные строители крупнейших телескопов, увидели Сириус В в только что налаженный 46 - сантиметровый телескоп. Орбиты Сириусов уточнили и с помощью обобщенного третьего закона Кеплера пару "взвесили". Но массу Сириуса А удалось оценить раньше косвенным путем - по известному расстоянию до него (2,66 парсека), светимости и спектральному классу.

Она равна М_А=2,3 M_⊗. Поэтому, даже не зная результатов Кларков, можно

Задача 22. Рассчитать массу Сириуса В, используя приведенные выше данные о Сириусе А. Считать, что орбиты Сириусов круговые, а плоскость орбит перпендикулярна направлению от них к Солнечной системе.

Вспомним, что парсек - расстояние, с которого радиус земной орбиты виден под углом 1", т. е. 206265 а. е." "2,06×10⁵ а. е. Так как Сириус А отклоняется от прямолинейного пути на 2,3", а земная орбита видна с Сириуса под углом (1/2,66)", радиус орбиты Сириуса, очевидноу r_А=2,66×2,3=6,12 а. е. Но это не величина а, входящая в формулу обобщенного третьего закона. Это только радиус окружности, по которой вокруг центра масс обращается Сириус А. Нетрудно выразить параметр а через массы Сириусов; получаем а=r_А(М_А+М_В)/М_В. Далее призываем читателя поработать самостоятельно.

Дальше по этому пути идти некуда. В нашей Солнечной системе самый близкий по массе к своей планете спутник у Земли. Но Луна все-таки в восемьдесят с лишним раз легче Земли, и в большинстве случаев ее можно считать "невесомой". Поэтому остается вообразить, что Задача 23. Земля внезапно стала по массе равной Солнцу, а расстояние между ними не изменилось. Как изменилась продолжительность года?

В пределах разумного мы исчерпали задачу двух тел. Проблема трех тел вообще пока не решена. Но "частная проблема трех тел", когда массой одного из них можно пренебречь, разрешима. Нам, например, посильна.

Задача 24. Звезды А и В α Центавра обращаются по круговым орбитам на некотором расстоянии друг от друга. Массы их практически равны. В той же плоскости вокруг центра масс звезд А и В обращается по окружности легкая планета С, причем треугольник ABC (рис. 8)

сохраняет свою форму и размеры. Найти радиус орбиты планеты С.

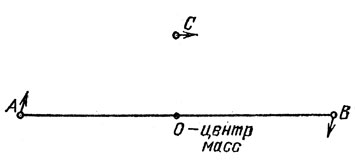
Рис. 8

Сразу отметим, что речь идет отнюдь не о Проксиме. Та далеко от АВ, а наша гипотетическая планета "влезла" внутрь системы звезд, и для нее они ни в коей мере не эквивалентны одному притягивающему центру.

Читатель, надеюсь, решил задачу 24 или, по крайней мере, ознакомился с ее решением по ОРЗ. Поэтому не будет нежеланной подсказкой упоминание о том, что в действительности подобные планеты существуют в нашей Солнечной системе. Оказывается, такое движение в вершине равностороннего треугольника, построенного на АВ, устойчиво и в том случае, если массы А и В различны. В частности, две группы астероидов движутся по орбите Юпитера (это нетрудно понять, если вспомнить, что Юпитер все же гораздо легче Солнца); одна из групп опережает Юпитер на 1/6 окружности, другая на такое же расстояние отстает от него. Это так называемые "троянцы": им присваивают имена участников Троянской войны - в одной группе греческие герои, в другой - защитники Трои.