Законы

 Если бы вся Вселенная обратилась в одно государство, 
 то как не установить повсюду одинаковых законов? 

К. Прутков

С точки зрения физики Вселенная - "одно государство", законы во Вселенной едины. Пример - закон всемирного тяготения. Но ведь это, в конце концов, только формула, описывающая одно из фундаментальных взаимодействий. Есть законы, которые еще более наглядно подтверждают формулировку Энгельса: "Закон - форма всеобщности".

Первый из них - закон сохранения энергии. Сфера его действия не ограничивается, конечно, кругом задач, которые могут быть рассмотрены в этой книге. Такого масштаба закон - результат общения невообразимой массы результатов наблюдений, экспериментов, теоретических изысканий. Ни из чего другого его не получишь. Часто встречаются утверждения, что законы сохранения можно получить из одних только свойств симметрии пространства и времени. Но даже те авторы, у которых за одиозным выражением "нетрудно показать" действительно следует доказательство, начинают его словами "если учесть ...", и далее следует второй закон Ньютона, третий закон...

Наша задача гораздо скромнее. Мы хотим найти конкретную форму закона сохранения энергии применительно к силам тяготения и научиться пользоваться этим законом. Вот в такой узкой постановке задачи нам кое- что удастся "показать". Еще уже: как выглядит формула для потенциальной энергии гравитационного взаимодействия двух материальных точек?

Потенциальная энергия - величина, не вполне определенная. Ясный смысл имеет только разность потенциальных энергий, а сама энергия зависит от того, какому состоянию мы припишем определенное, произвольно выбранное нами значение энергии. Если два тела бесконечно удалены друг от друга, то они, конечно, не взаимодействуют. Поэтому естественно этому состоянию приписать нулевое значение потенциальной энергии. При любом конечном расстоянии между телами в этом случае энергия будет отрицательной величиной: чтобы "растащить" тела до бесконечного расстояния между ними, надо совершить работу, добавить энергию.

Еще раз хочу подчеркнуть, что основной аргумент в пользу такого выбора - нам так удобно. Вряд ли кто- нибудь одобрит такой выбор, если ему предстоит рассчитать, на какую высоту он может забросить камень, даже если это очень сильный метатель. Тут естественно нулевое значение энергии выбрать на поверхности Земли, как это чаще всего и делается при решении подобных задач.

Проще всего получить энергию, вычислив работу, т. е. проинтегрировав величину GMm/r² от расстояния R до бесконечности. Получаем U=-GMm/r.

Читателю, не знакомому с интегрированием, может помочь аналогия с электростатическим взаимодействием. В законе Кулона тоже фигурирует обратная пропорциональность силы расстоянию, и выражение для энергии отличается от выражения для силы только тем, что расстояние в знаменателе меняет степень с двух на единицу. Знак тоже понятен - сила притяжения соответствует разноименным зарядам, и соответствующая энергия отрицательна.

Несколько слов о материальных точках. Когда мы рассматривали, допустим, систему Сириуса, там все понятно: размеры звезд несравненно меньше расстояния между ними, и неважно, что эти "материальные точки" имеют диаметры по десятку тысяч, и то и по миллиону километров. Когда правомерность такого приближения казалась сомнительной, были сделаны соответствующие оговорки, как в задаче о Проксиме. Но мы и движение спутника по стелющейся траектории рассматривали так, как будто звезда - материальная точка. А тут размеры тела и расстояние между телами в лучшем случае равны-если считать от центра звезды. А откуда надо считать?

Вспомним: еще Ньютон доказал, что в случае сферически симметричного распределения плотности внутри тела последнее действует на другие тела точно так же, как материальная точка массы, равной массе этого тела, расположенная в его центре. Как он это доказал? Вычислил, как мы вычислили силу в задаче с планетой, взаимодействующей с двумя звездами. Только ему пришлось разбить шар на бесконечное число бесконечно малых частей, которые уже можно считать точками, и проинтегрировать.

Одно вспомогательное мероприятие. Полезную для решения более содержательных задач формулу нас заставит получить

Задача 25. Найти потенциальную энергию тела единичной массы на поверхности Земли, зная g₀ и r₀.

Эту формулу нетрудно получить, сравнивая выражения для потенциальной энергии и для силы притяжения к Земле mg₀. Оказывается, U/m=-g₀r₀.

Примечательно, что по абсолютной величине эта энергия ровно в два раза больше кинетической энергии единицы массы спутника, движущегося по стелющейся орбите. Можете проверить: мы уже вычисляли скорость такого спутника - первую космическую скорость. Если мы вспомним еще раз, что кинетическая и потенциальная энергии у нас имеют разные знаки, то сразу получим, что полная энергия равна по модулю кинетической, но отрицательна.

Эти простые соотношения, как нетрудно проверить, справедливы для любого тела, движущегося по окружности вокруг притягивающего центра. Необходимо только, чтобы сила убывала пропорционально квадрату расстояния. Например, такие же соотношения между различными видами энергии справедливы для электрона, который движется по окружности в кулоновском поле ядра: U=2E=-2K.

Но вернемся к нашей любимой гравитации.

Задача 26. Ракета запущена с первой космической скоростью точно по направлению от центра Земли. На какую высоту она поднимается?

Если бы мы запустили ракету горизонтально, она стала бы спутником (про сопротивление воздуха забудем). Но в любом случае она движется по эллипсу. Окружность - вырожденный эллипс с совпадающими фокусами. В нашем случае эллипс вырождается в отрезок прямой,- это эллипс, у которого фокусы "убежали" на самые края, на концы отрезка. В данный момент эти замечания не очень актуальны, но они нам еще пригодятся. Теперь о задаче 26. Как мы только что выяснили, полная энергия ракеты в расчете на единицу массы будет равна - g₀r₀/2. На произвольном расстоянии R от центра Земли потенциальная энергия уменьшится в R/r₀ раз и будет равна -g₀r₀²/R. Кинетическая энергия в момент наивысшего подъема, очевидно, равна нулю. Следовательно, ... см. ОРЗ.

Значит, как и надо было ожидать, с первой космической скоростью можно попасть только в самый ближний космос. А какая скорость нужна, чтобы улететь от Земли?

Задача 27. Рассчитать вторую космическую скорость.

На Земле потенциальная энергия равна -g₀r₀ на бесконечности она равна нулю. Значит, чтобы добраться до бесконечности, хотя бы "доползти" туда с нулевой скоростью, надо иметь запас кинетической энергии, равный g₀r₀ (все энергии берутся в расчете на единицу массы).

При вычисленной нами скорости - 11,18 км/с - тело "убежит" от Земли по параболе. Поэтому вторая космическая скорость имеет еще два названия - "скорость убегания" и "параболическая скорость". В общем случае мы будем употреблять последнее название, например "для тела, находящегося в поле тяжести звезды Бетельгейзе на расстоянии 1000 а. е. от ее центра, параболическая скорость равна...". Если тело находится на поверхности планеты, например Юпитера, или звезды, мы будем говорить: "Скорость убегания для Юпитера равна...". А название "вторая космическая скорость" прибережем для скорости убегания с Земли, для параболической скорости на поверхности Земли.

А между прочим, действительно,

Задача 28. Чему равна скорость убегания для Юпитера? M_ю=318 М₀, r_ю=11 r₀.

Или вот еще

Задача 29. Чему равна параболическая скорость на расстоянии 1 а. е. от Солнца?

Мы, наверное, уже заметили, что параболическая скорость в √2 раз больше соответствующей круговой. Поэтому достаточно просто умножить на √2 скорость движения Земли по своей орбите.

Подчеркнем, что это отнюдь не третья космическая скорость. Третьей космической скоростью называют скорость, которую тело должно иметь у поверхности Земли, чтобы потом оно смогло уйти не только из поля тяготения планеты, но из поля тяготения Солнца, т. е. смогло покинуть Солнечную систему. Как рассчитать эту скорость?

Задача 30. Чему равна третья космическая скорость?

Покинув поле тяготения Земли, тело должно иметь параболическую скорость - 42,1 км/с - относительно Солнца. Но Земля движется относительно Солнца со скоростью 29,8 км/с. Значит, при удачном выборе направления телу достаточно иметь скорость относительно Земли 12,3 км/с. А на поверхности Земли? (См. ОРЗ.)

Пожалуй, стоит пояснить слова "покинет поле тяготения" той или иной планеты, звезды.

Строго говоря, поле тяготения любого тела простирается до бесконечности. Какое бы расстояние мы ни выбрали, все равно получим некоторое конечное значение силы. Пример влияния Юпитера на движение кометы Галлея в поле тяготения Солнца мы разбирали на с. 13. И, кстати, видели, что Юпитер с помощью Сатурна и всех других планет за два с лишним тысячелетия изменил период обращения кометы лишь на пару процентов.

Так что есть много случаев, когда влиянием всех тел, кроме одного, можно с какой-то степенью точности пренебречь.

Так вот, мы при анализе движения тела вблизи планеты пренебрегаем воздействием Солнца, не забывая при этом двух обстоятельств. Во-первых, мы рассматриваем движение тела относительно, например, Земли, и полученная нами на первом этапе скорость - скорость относительно Земли, а никак не относительно Солнца или, тем более, относительно "неподвижных звезд". И второе: как только тело достаточно далеко ушло от Земли, его судьба - в руках Солнца. Что такое "достаточно далеко"?

В большинстве случаев мы не допустим серьезных просчетов, если будем рассматривать в подобных случаях движение под действием только той силы, которая в данном месте больше. Особые случаи, например приливные силы, надо рассматривать подробнее, учитывая взаимодействие одновременно с двумя телами. Так мы уже делали, например (хотя рассматривали не приливы) в задаче с придуманной планетой С в системе а Центавра.

Как мы только что вспомнили, комета Галлея движется практически только йод влиянием Солнца. Не удастся ли нам оценить,

Задача 31. Какова максимальная скорость кометы Галлея?

Очевидно, что максимальной скорость кометы будет на минимальном расстоянии от Солнца. Вспомним, что оно равно 0,59 а. е. После "свидания." со светилом комета уходит очень далеко от него. Не на бесконечность, но очень далеко. Значит, ее полная энергия не равна нулю, но ненамного меньше нуля. Но тогда скорость в перигелии хотя и не равна параболической, но близка к ней. Нас просят оценить скорость кометы. Параболическая скорость для расстояния 0,59 а. е., по-видимому, будет не очень грубой оценкой.

Уточнением этой скорости мы вскоре займемся, а сейчас - о других законах.

Второй великий закон - закон сохранения импульса, количества движения. Им мы тоже широко будем пользоваться. Пример:

Задача 32. Спутник движется вокруг планеты со скоростью υ. Он состоит из двух отсеков равной массы. В некоторый момент времени отсеки разделяются, причем один из них останавливается. Какова скорость второго отсека сразу после разделения?

Можно ли при решении этой задачи использовать закон сохранения энергии? Конечно, нет. На разделение отсеков была затрачена какая-то работа: может быть, космонавты отталкивали отсеки друг от друга (что маловероятно), скорее всего, один отсек, как говорится, отстреливали от другого - тогда надо учесть химическую энергию. Ведь полное название "главного" закона природы: закон сохранения и превращения энергии.

А импульс сохранится? Ответим уклончиво: законом сохранения импульса пользоваться можно.

Строго говоря, импульс сохраняется в двух случаях:

1. если система замкнута, т. е. внешних сил нет;
2. если внешние силы уравновешивают друга друга.

У нас ни один из этих вариантов не осуществляется - есть сила притяжения к планете, которая ничем не уравновешивается. Почему же мы собираемся применять несправедливый в данном случае закон?

Вот тут надо разделить два случая, назовем их "отстрел" и "ручной" способ. При отстреле между отсеками действует очень большая сила, но действует она недолго. Получается, что эта, внутренняя для спутника в целом, сила успевает заметно изменить относительное движение частей корабля, в то время как умеренная по величине сила притяжения за столь короткое время не может внести существенных изменений в движение отсеков, в движение корабля в целом, в движете его центра масс.

Другое дело - ручной способ. Скоро ли удастся затормозить полспутника до полной остановки? Если отсек имеет массу, предположим, всего 1 тонну, то три-четыре космонавта в лучшем случае могут развить "внутреннюю силу" порядка силы тяжести (если планета - Земля). Пока они будут стараться, сила тяжести тоже поработает, и что там получится, сразу и не сообразишь.

Но, может быть, можно, считая, что центр масс движется по прежней траектории, пересесть в связанную с ним систему отсчета и там все рассчитать? Иногда можно, но не всегда. Пока мы расталкиваем отсеки, меняются не только их скорости, но и положения. Если мы продолжаем решать нашу не слишком серьезную задачу о "ручном" способе разделения отсеков, то такой вариант решения надо признать корректным. В общем же случае, так как иоле тяжести неоднородно, внутренние силы, меняющие взаимное расположение частей, могут вызвать изменение суммарной внешней силы, действующей на спутник, а значит, и движения центра масс.

Ситуация здесь такая же, как при "езде на стуле". Упрощенно этот захватывающе интересный способ пере-движения можно представить примерно так. Подпрыгнув вместе со стулом, мы его (стул) "проталкиваем" под собой немного вперед. Потом, пока стул стоит на полу, мы сползаем на передний край стула, который силами трения удерживается на месте, и повторяем все сначала. Мы лично взаимодействуем только со стулом, для системы "стул - человек" наши усилия - внутренние силы. Но в результате этих усилий меняется сила трения между стулом и полом - внешняя сила, что и позволяет нам вместе со стулом передвигаться.

Можно ли "ездить на стуле" в космосе? Оказывается, можно. Подобный способ передвижения рассматривается вполне серьезно, действующее на этом принципе устройство даже имеет название - "гравилет", хотя еще и не построено.

Но о гравилете мы поговорим позже А сейчас нас ждет третий великий закон.

Это закон сохранения момента импульса. Собственно говоря, мы с ним уже отчасти знакомы. Второй закон Кеплера - частный случай закона сохранения момента импульса. Что такое момент импульса? Существует тесная связь между моментом силы и моментом импульса. Как момент силы - произведение силы на плечо, так и момент импульса - произведение импульса на плечо. Более того, точно так же, как внешняя сила изменяет импульс, момент внешних сил изменяет момент импульса. Скорость изменения импульса равна внешней силе, скорость изменения момента импульса равна моменту внешних сил.

Где же тут второй закон Кеплера?

Посмотрим на рис. 9. Для простоты выбраны точки, где векторы υ и r перпендикулярны друг другу, т. е. точки, где r - плечо. Сила проходит через ось - мы специально, конечно, выбрали ось, проходящую через центр притяжения,- и момента не создает. Момент импульса планеты не должен изменяться. Но что такое момент импульса? Это произведение mυr. Умножив его на величину некоторого небольшого промежутка времени т и разделив на удвоенную массу, получим "площадь, заметаемую радиусом-вектором планеты за время m". Постоянство этой площади и есть второй закон Кеплера.

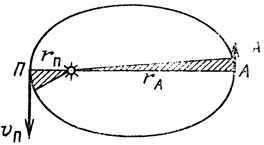
Рис. 9

Достаточно ясно, что и в произвольной точке произведение момента импульса на половину плеча, деленное на массу тела, есть площадь треугольника, заметаемого радиусом-вектором за единицу времени.

Несколько сложнее обстоит дело в случае сравнимых масс взаимодействующих тел - двойные звезды, пары галактик. Конечно, и в этом случае момент импульса сохраняется, но применение закона приводит к утомительно громоздким выкладкам. Поэтому в двойных системах мы будем рассматривать только круговые орбиты, где все гораздо проще.

Мы вспомнили три великих закона природы. Теперь мы знаем все, что нам надо для решения собранных в этой книге задач.

Конечно, одними законами не обойтись. Они только отвечают на вопрос, что может быть. То, что противоречит этим законам, "не может быть, потому что не может быть никогда". А что будет?

Ну, например, тело имеет вторую космическую скорость. Оно может улететь от Земли.

А улетит ли? Надо еще посмотреть, куда эта скорость направлена. Вспомним, что первая космическая скорость делает тело спутником Земли, только если она направлена горизонтально относительно поверхности Земли. У второй космической скорости свободы побольше. Если тело сразу не врежется в Землю, значит, будет от нее удаляться. Поэтому достаточно, чтобы направление скорости составляло острый угол (в крайнем случае - прямой) с нормалью к поверхности Земли, и мы на свободе - в открытом космосе.

Но вернемся к нашим планетам. Впрочем, сначала к комете Галлея. За автором должок, который как раз пора отдать, что я и постараюсь сделать, предлагая читателю заняться "ловлей блох".

Задача 33. Уточнить значение скорости кометы Галлея в перигелии, используя закон сохранения энергии и закон сохранения момента импульса (второй закон Кеплера).

Рассмотрим перигелий и афелий орбиты - воспользуемся рис. 9. Расстояния r_п и r_a мы знаем - 0,59 и 35,5 а. е. (задача 4). Запишем два рекомендованных к использованию закона для этих точек и заглянем в ОРЗ.

Не правда ли, немного обидно - насколько больше вычислений, чем в задаче 31, а отличие результатов едва ли в пределах точности расчетов? Зато совсем немного надо считать, чтобы.

Задача 34. Вычислить скорость кометы в афелии.

Жаль расставаться с такой замечательной кометой, поэтому еще.

Задача 35. Какое время тратит комета Галлея на прохождение ближней к Солнцу половины орбиты?

Кто не помнит площадь эллипса - она равна πab, где а и b - соответственно большая и малая полуоси.

Что-то мы увлеклись вычислениями. А ведь гораздо лучше нас, во всяком случае, лучше автора, это делали великие вычислители.

В каждой науке ровно столько истины,
 сколько в ней математики. 

И. Кант

Небесная механика - так называется область науки, по окраинам которой мы бродим в этой книжке. И в этой области полно математики.

Первой крупной победой этой науки было предсказание возвращения кометы Галлея. Но подлинным ее триумфом стало открытие, как сказал Энгельс, "на кончике пера" новой планеты - Нептуна.

К XVIII веку семейство планет по сравнению о древностью уменьшилось - Луну "разжаловали" в спутники, Солнце "возвели в сан" главы семьи. Но вот в 1781 году произошло первое "прибавление семейства": Уильям Гершель открыл Уран. В общем-то удивительно, что это произошло лишь спустя 170 лет после того, как Галилей впервые посмотрел на небо в телескоп. Конечно, Уран вдвое дальше Сатурна, в два с половиной раза меньше его, но все же светит, как звезда 6-й величины, т. е. на пределе видимости даже для невооруженного глаза.

Как бы то ни было, новая планета была открыта. И тут началась, вероятно, известная читателю история. Уран упорно не желал подчиняться законам Кеплера, даже с учетом возмущений, которые вносят все планеты.

Возник вопрос: а все ли? Может быть, существует еще более далекая планета, которая практически не влияет на движение всех планет, кроме Урана??

Англичанин Адамс и француз Леверье почти одно-временно решили обратную задачу небесной механики: по известным отклонениям Урана от "правильного пути" вычислили траекторию "возмутителя".

Адамсу не повезло. Хотя он закончил свои расчеты на несколько месяцев раньше Леверье, планету никто не искал. Руководителя Адамса работа не заинтересовала, и она легла под сукно. А по расчетам Леверье был найден и опознан Нептун. Напомню, что никаких ЭВМ в то время (Нептун был открыт 24 сентября 1846 года) не было, Адамс и Леверье вручную численными методами - другие для такой задачи не подходят - решали громоздкую систему уравнений. Поистине титанический труд!

Итак, самая далекая из планет - Плутон. Так, да не совсем. И речь не о том, что, может быть, за Плутоном есть еще планеты. Тогда достаточно было бы уточнить - из известных планет. А речь о том, что

Задача 36. Из-за сравнительно большого эксцентриситета орбиты Плутона (большая полуось а=5,9×10⁹ км, малая полуось b=5,73×10⁹ км) его расстояние от Солнца меняется от минимального r=4,4×10⁹ км до максимального R=7,4×10⁹ км. Нептун же движется по практически круговой орбите радиуса R₁=4,5×10⁹ км. В результате часть орбиты Плутона, определяемая углом α=100° (см. рис. 10), расположена ближе к Солнцу, чем орбита Нептуна. В 1969 году Плутон перешел с девятого на восьмое место среди больших планет Солнечной системы. Когда он вернется на свое законное девятое место?

Период обращения Плутона, конечно, можно определить из третьего закона Кеплера. Получаем Т=247 лет. А нашу задачу поможет решить второй закон Кеплера (см. ОРЗ).

Мы до сих пор занимались почти исключительно естественными небесными телами. Если изредка в задачу и попадал спутник, то какой-то безымянный. А между тем в небо рвались совсем не безымянные.