Икары

 Земля - колыбель человечества. 
 Но нельзя же вечно жить в колыбели! 

К. Э. Циолковский

Космическая эра начиналась дважды. Только что исполнилось 30 лет со дня запуска первого искусственного спутника Земли - он взлетел 4 октября 1957 года. А пока книга дойдет до читателя, на очереди будет тридцатилетие первого космического полета человека.

12 апреля 1961 года первый Икар XX века поднялся в космос. Имя его известно всем - это Юрий Гагарин, первый человек, облетевший Землю.

А сколько времени понадобилось Ю. А. Гагарину, чтобы совершить кругосветное путешествие?

Задача 37. Орбита космического корабля "Восток" имела высоту в перигее 181 км, а в апогее - 327 км. Определите период обращения космического корабля Ю. А. Гагарина вокруг Земли.

Наверное, проще всего сначала вычислить период обращения по стелющейся орбите: мы знаем длину окружности земного шара - 40 тыс. км, а первая космическая скорость - 7,9 км/с - скорость спутника на приземной орбите. Значит, минимальный (теоретический, без учета сопротивления воздуха) период спутника - 5064 с=1 ч 24,4 мин. С помощью третьего закона Кеплера без труда получим, что период обращения "Востока" равен почти точно полутора часам. Напомним, что в действительности Гагарин находился в полете 1 ч 48 мин, т. е. он пролетел несколько больше одного "витка"

И полетели спутники! Сначала - чтобы посмотреть, как там в космосе, потом - чтобы работать на человека. С 1965 года работают советские спутники связи "Молния". Одной из самых удобных для связи является так называемая геостационарная орбита - когда спутник все время "висит" над одной точкой земной поверхности.

Задача 38. Определить радиус орбиты геостационарного спутника.

Конечно, такой спутник должен обращаться в плоскости экватора.

Множество спутников запущено за 30 лет космической эры. Некоторые из них движутся по близким орбитам. Мы рассмотрим.

Задача 39. Два спутника, которые движутся по одной орбите, имеют период обращения вокруг Земли 4 часа. Расстояние между спутниками изменяется от минимального - 2 км до максимального - 5 км. Определить высоту апогея и перигея общей орбиты спутников.

В марте 1965 года первый человек - Алексей Леонов - побывал в открытом космосе. Один из экспериментов, которые он там произвел, привел к запуску спутника в буквальном смысле слова рукой человека: он бросил крышку фотоаппарата, и она стала самостоятельным спутником Земли.

Но прежде чем изучить движение крышки-спутника, мы вспомним две формулы, которые здорово нам могут помочь.

Формула первая, точная.

Задача 40. Выразить большую ось орбиты спутника через его полную энергию.

Для круговой орбиты, используя выражение для центростремительной силы, легко получим 2a=2R=GM/K (К - кинетическая энергия). Теперь вспомним, что полная энергия по модулю равна кинетической; значит, 2a=GM/|E|. Для эллиптической орбиты результат тот же. Вывод посложнее, он приведен в ОРЗ.

Формула вторая, приближенная - не из физики, а из математики. Допустим, в выражении (1+x)ⁿ второе слагаемое в скобках - x - мало по сравнению с единицей. Если n - целое число, то (1+x)ⁿ=1+nx+n(n-1)x²/2+...+... Но каждый следующий член примерно в 1/x раз меньше предыдущего. Значит, если не гнаться за абсолютно точной цифрой, а в физике таких не бывает, то на каком-то члене этот ряд можно оборвать. Мы обычно будем его обрывать на втором члене, т. е. считать, что (1+x)ⁿ=1+nx. Заметим, что эта приближенная формула справедлива для любых показателей степени - отрицательных, дробных, иррациональных.

Теперь мы готовы бросать крышки со спутников. Для начала?

Задача 41. Бросим крышку вперед по ходу спутника, находящегося на околоземной орбите. Скорость крышки (относительно спутника, конечно) υ_k = 10 м/с. Насколько орбита крышки отличается от орбиты спутника?

Вопрос сформулирован нечетко. Это сделано умышленно чтобы читатель сам попытался разобраться какой будет орбита.

Если форма и параметры орбиты крышки прояснились, нетрудно вычислить,

Задача 42. Каково будет расстояние между крышкой и спутником, когда они совершат один оборот после запуска крышки?

А теперь посмотрим, что сделал Леонов.

Задача 43. Леонов бросил крышку по направлению к центру Земли. Скорость крышки относительно корабля та же - 10 м/с. Насколько отличается большая полуось орбиты "крышки Леонова" от радиуса орбиты спутника (который считать практически равным радиусу Земли)?

 Хуже нет - ждать да догонять. 

Русская пословица

Мы немного научились сравнивать мало отличающиеся орбиты. В задаче 41 один из спутников - крышка - пытался убежать от другого; в задаче 42 орбиты пересекались. Вернемся к задаче 39. Там один из спутников безуспешно гнался за другим, то приближаясь к нему, то отставая.

А что надо сделать, чтобы спутники состыковались? На первый взгляд, совсем простую вещь: увеличить скорость "заднего" спутника, он догонит передний, тогда чуть притормозим - и вот она, мягкая стыковка.

Не тут-то было. Увеличив скорость второго спутника, мы забросим его на другую, более высокую орбиту. Для простоты рассмотрим случай, когда спутники летят друг за другом по круговой траектории. После ускорения второй спутник станет двигаться по эллипсу, для которого точка ускорения - перигей, и проскочит мимо первого (рис. 11). Общей у их траекторий теперь будет одна точка II. Только там они могут встретиться. Как же им оказаться в этой точке одновременно?

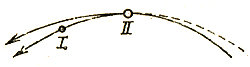
Рис. 11

Первый спутник попадет туда через время, немного меньшее, чем первоначальный период обращения обоих спутников. А второй? Ему нужен целый период, да к тому же период новый, период обращения по эллиптической орбите, на которую он попал после ускорения. А этот период больше первоначального. Ускорившийся второй спутник отстанет еще больше от "ленивого" первого!

Вот теперь не покажется неожиданным вариант: чтобы догнать, надо ... притормозить!

Задача 44. Два спутника движутся по одной круговой орбите радиуса 7000 км на расстоянии 53 км друг от друга. При каком изменении скорости второй спутник через период догонит первый?

Еще совсем незадолго до начала космических полетов, даже уже после запуска первых спутников, одним из вероятных препятствий для прорыва в космос человека считалась метеоритная опасность.

Действительно, открыты тысячи астероидов - глыб размером в сотни километров. "Камушек" в десяток метров и в самый мощный телескоп не углядишь. А какого размера метеорит опасен для спутника? Конечно, это в значительной мере зависит от того, куда этот камушек попадет. Важна и скорость камня. Если он догоняет спутник - допустим, это тоже спутник Земли, вроде крышки,- то относительная скорость может быть небольшой, произойдет "мягкая стыковка". Но пред-положим, что это спутник Солнца, который движется примерно по орбите Земли, но в противоположную сторону. И вот он подлетает к Земле.

Задача 45. Какова будет скорость такого метеорита относительно Земли вблизи ее поверхности?

И вот такой "скоростной" метеорит попадает в космический корабль. Что будет? Допустим, космонавты не пострадали; они в скафандрах, так что и утечка воздуха им не страшна. Но орбита?

Задача 46. Спутник массы в 1 тонну движется по круговой орбите, радиус которой в 2 раза больше радиуса Земли. Метеорит из задачи 45 сталкивается со спутником "лоб в лоб" и застревает в кем. При какой массе метеорита спутник врежется в Землю?

Но меняют орбиты не только крышки или, упаси бог, сбитые с пути метеоритами спутники. Сами спутники, межпланетные корабли совершают многочисленные