Странный маятник (Н. Минц)

Обычный, хорошо знакомый вам математический маятник не меняет плоскости своих колебаний.

На этом свойстве маятника основана известная демонстрация вращения Земли - опыт Фуко. Маятник на длинном подвесе совершает колебания. Под ним размечен круг, напоминающий циферблат. Благодаря тому, что плоскость колебаний маятника относительно неподвижных звезд не меняется, а Земля вращается вокруг своей оси, с течением времени маятник проходит последовательно над всеми отметками круга. На полюсе за сутки круг под маятником совершит полный оборот. Впервые такой опыт был проведен французским физиком Л. Фуко в 1851 году под куполом Пантеона в Париже с маятником длиною 67 м.

Но всякий ли маятник обязательно сохраняет плоскость колебаний? Ведь нить подвеса позволяет ему колебаться в любой вертикальной плоскости.

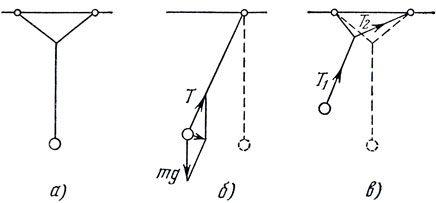
Рис. 80

Попробуйте сделать такой маятник, как показано на рис. 80, а. Для этого возьмите нитку, сложите ее пополам, а к середине привяжите еще одну нитку. К другому концу этой второй нитки прикрепите ложку, ножницы или какой-нибудь другой предмет - и маятник готов. (Вертикальная нить подвеса должна быть достаточно длинной. По крайней мере не меньше, чем нить наклонного подвеса.)

Подвесьте маятник за оба конца сложенной пополам нитки на кнопках или гвоздиках (например, в дверной проем). Если теперь отклонить маятник от положения равновесия и затем отпустить, то вы увидите любопытную картину. Маятник будет двигаться по эллипсу, причем этот эллипс будет постоянно меняться, вытягиваясь то в одну, то в другую сторону. Почему это происходит?

У маятника с одной точкой подвеса (рис. ©и, и) плоскость колебаний ничем не выделена. Каким бы ни было первоначальное отклонение маятника, все силы, действующие на него, лежат в одной плоскости. Нужно только, отпуская маятник, не толкнуть его вбок.

Действительно, проведем плоскость через первоначальное и отклоненное положение маятника. Очевидно, в этой плоскости будут лежать как сила тяжести mg, так и сила натяжения нити Т. Следовательно, равнодействующая этих сил, которая, собственно, и заставляет маятник колебаться, при любом отклоненном положении маятника также лежит в той же плоскости. Это означает, что нет сил, которые могли бы вывести маятник из этой плоскости. Потому-то маятник и сохраняет плоскость своих колебаний.

Другое дело наш маятник. Здесь точками закрепления и линией отвеса строго фиксирована первоначальная плоскость. Поэтому с самого начала маятник отклонен так, что он не лежит в этой плоскости^*. Сила натяжения (рис. 80, в) имеет составляющую, перпендикулярную первоначальной плоскости. Благодаря этой составляющей движение маятника выходит из первоначальной плоскости. При этом, поскольку сила натяжения не постоянна, меняется и ее перпендикулярная составляющая. Далее, отклоняясь в противоположную сторону, маятник натягивает другую из закрепленных нитей. Это приводит к появлению силы, действующей в другом направлении. При этом, как показывает опыт, и возникает движение по двум взаимно перпендикулярным направлениям.

^* (Конечно, если отклонить маятник строго перпендикулярно плоскости подвеса, он будет совершать колебания в одной плоскости, перпендикулярной

плоскости подвеса. Но практически всегда существуют отклонение от перпендикуляра и скорость, не лежащая в плоскости первоначального отклонения.)

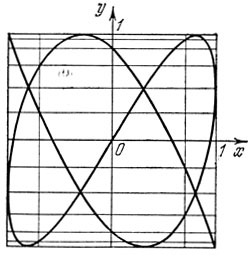
Рис. 81

Кривые, которые описывает наш маятник, называются фигурами Лиссажу, по имени французского физика Лиссажу, который в 1863 году впервые описал их. Фигуры Лиссажу получаются при сложении двух взаимно-перпендикулярных колебаний. Они могут быть довольно сложными, особенно при близких частотах продольных и поперечных колебаний. Если частоты одинаковы, траекторией движения будет эллипс. Фигура, показанная на рис. 81, описывается маятником, уравнения движения которого выглядят следующим образом: х = sin 3t, y = sin 5t. Рис. 82 соответствует колебаниям x = sin 3t, y = sin 4t.

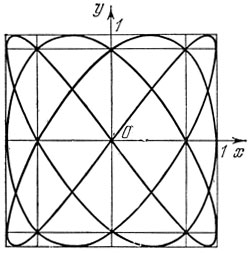
Рис. 82

Соотношение частот можно варьировать, меняя отношение длин вертикальной и наклонной нитей подвеса. При этом вычислить частоты колебаний маятника довольно сложно, а вот увидеть фигуры, вычерчиваемые им, значительно проще.

Для того чтобы увидеть фигуры Лиссажу, можно к подвесу нашего маятника прикрепить ведерко с дырявым дном, наполненное песком, а на пол положить кусок картона, окрашенный в темный цвет. Тогда маятник "нарисует" отчетливую траекторию своего движения.

Можно получить фотографии траекторий движения маятника. Возьмите грузило или тяжелый маленький шарик и покрасьте его белой краской. Сделайте из темных ниток такой же подвес, как у маятника, изображенного на рис. 80, а. Под маятник подложите лист черной матовой бумаги. Гладкая бумага может отсвечивать, а это будет мешать наблюдениям. Фотографировать надо сверху. Установите фотоаппарат так, чтобы плоскость объектива была горизонтальна. При достаточно большой выдержке на фотоснимках можно увидеть четкие траектории.

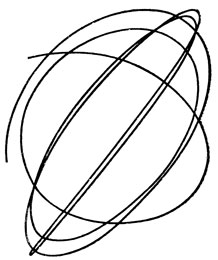
Рис. 83

На рис. 83 и 84 приведены рисунки с фотографий траекторий, полученных таким способом. Видно, как маятник изменял направление колебаний. На фигуре рис. 83 это изменение произошло более резко. Время экспозиции этих двух фотографий различно. Это видно хотя бы из того, что длина траекторий неодинакова.

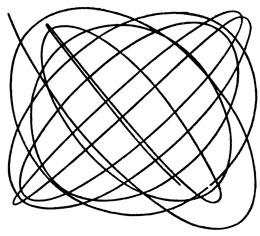
Рис. 84

Получившиеся кривые как бы вписаны в параллелограмм. На самом деле они должны быть вписаны в прямоугольник. То, что у нас не получился прямоугольник, объясняется просто: плоскость объектива была не строго горизонтальна.

В опытах с маятником следует учитывать, что более или менее правильная траектория получается только в том случае, когда нет сильных затуханий. Колебания маятника с малой массой груза и достаточно большим объемом будут быстро затухать. Такой маятник качнется несколько раз, быстро уменьшая амплитуду. Естественно, при движении с сильным затуханием увидеть и сфотографировать изменение направления колебаний маятника не удастся.

С фигурами Лиссажу приходится встречаться довольно часто в тех случаях, когда колебания взаимно перпендикулярны. Так, они неизбежно появляются при настройке осциллографа.