Волны в мелкой тарелке (интерференция) (А. Косоуров)

Нет в природе явления более универсального, чем распространение волн. Волны на поверхности воды, звук, свет, радио, передача деформации от одних частей твердого тела к другим - все это волновые процессы. Квантовая механика показывает, что и движением микрочастиц управляют волновые законы. Все эти волны имеют разную физическую природу, разные скорости распространения, разные частоты и длины волн. Но независимо от этого в движении любых волн много общего. Изучив законы распространения волн одной природы, можно большинство из них практически без изменения перенести на волны другого типа. Изучать же волны удобнее всего на поверхности воды.

Что такое волна? Бросьте в пруд камень. На спокойной горизонтальной поверхности пруда возникнут разбегающиеся круги. Точки поверхности воды, до которых дошла волна, начинают колебаться относительно своего равновесного положения. Это положение соответствует горизонтальной поверхности. Чем дальше находится точка от места падения камня, тем с большим запозданием "узнает" она о падении камня. Возмущение распространяется с определенной скоростью. Точки, до которых возмущение дошло одновременно, находятся в одинаковой стадии колебательного движения (в одинаковой фазе).

Для волн любой природы всегда можно указать физические объекты, которые под действием волны испытывают возмущение, т. е. отклонение от своих равновесных значений. Для звука - это периодические повышения и понижения давления. Для радиоволн и света - быстрые изменения напряженности электрического и магнитного полей.

Свойства всех без исключения сред таковы, что возмущение, возникшее в некоторой области, распространяется, передаваясь от точки к точке с конечной скоростью, которая зависит от природы возмущения и свойств среды.

Для возникновения волны необходим источник возмущения, т. е. внешняя причина, вызывающая в некоторой области среды нарушение равновесия. Источник малого размера, как, например, камень брошенный в воду, излучает в однородной среде (т. е. в такой среде, в которой скорость волны не зависит от направления ее распространения) сферические волны (на поверхности воды - круговые), распространяющиеся по радиусам. Такие источники волн называют точечными.

Один из основных принципов элементарной волновой теории - принцип независимости волн, или принцип суперпозиции. Он утверждает, что возмущение, которое вызывает волна в точке наблюдения, не зависит от того, что через эту точку одновременно проходят другие волны. Принцип суперпозиции дает простое правило для нахождения суммарного действия волн от нескольких источников: суммарное колебание просто равно сумме колебаний, вызываемых каждым источником в отдельности.

Характерная особенность волновых процессов - интерференция волн. Интерференцией называют совокупность явлений, возникающих в среде при распространении волн от двух или нескольких источников, колеблющихся согласованно (синхронно). При этом оказывается, что в некоторых точках среды колебания, вызванные одновременным действием двух источников, будут сильнее или слабее, чем колебания, вызванные каждым источником в отдельности. Может случиться, что согласованные волны вообще погасят одна другую.

Постараемся посмотреть на интерференцию собственными глазами. Искушенный глаз без труда увидит интерференцию при пересечении волн от двух брошенных в пруд камней. Однако для изучения интерференции этот способ не годится. Мы получим устойчивую интерференционную картину водяных волн на лабораторном столе.

Прежде всего необходим сосуд с водой. Чтобы волны, отраженные от его стенок, не маскировали волн, идущих от источников, нужен сосуд с пологими стенками. В этом отношении хороша обыкновенная мелкая тарелка, в которую вода наливается почти до самого верха. Набегая на стенки, волны быстро затухают и почти не отражаются. Генератором волн может служить электрический звонок с отвинченным колпачком. К молоточку звонка прикрепите кусок проволоки, на ее конец наденьте пробковый шарик, который и будет точечным источником волн. Проводя опыты, следите за тем, чтобы провода были хорошо изолированы.

Звонок нужно укрепить над тарелкой так, чтобы поворотом звонка можно было погружать пробковый шарик в воду у края тарелки. Питать звонок лучше всего через автотрансформатор. Это позволит регулировать амплитуду колебаний. Очень удобен автотрансформатор от детской железной дороги. Подойдет и трансформатор от прибора для выжигания. Включив устройство, мы увидим на поверхности воды круговые волны с расстоянием между соседними горбами - длиной волны - около 1 см (рис. 95).

Рис. 95

Наблюдать волны лучше всего по тени на дне тарелки при прямом солнечном свете или свете яркой лампы. Каждая волна, действуя как цилиндрическая линза, дает на дне тарелки светлую полосу, повторяющую форму фронта волны. Однако волны, бегущие со скоростью около 10 см/с, сливаются для взгляда, фиксированного на неподвижной тарелке. Они видны только вблизи источника, где их амплитуда велика. Чтобы увидеть их на всей поверхности воды, нужно быстро поворачивать голову. Точно так же при быстрых движениях головы можно рассмотреть спицы катящегося колеса. Очень эффектными кажутся волны на матовом стекле фотоаппарата, особенно крупноформатного. Держа камеру в руках и плавно покачивая ее, легко добиться, чтобы волны были видны на всей поверхности. При этом кажется, что они бегут очень медленно. Можно смотреть на отражение поверхности воды и в зеркале. Легкие движения зеркала также делают волны видимыми по всей поверхности. Но удобнее всего наблюдать волны при стробоскопическом освещении. Если освещать установку короткими вспышками света с частотой, равной частоте источника волн, то от одной вспышки до другой волны переместятся на одну длину волны, и волновая картина волн будет казаться неподвижной. Такое освещение чрезвычайно легко осуществить. Достаточно параллельно обмоткам магнита звонка включить небольшую лампочку. С расстояния 0,5-1 м она хорошо и равномерно осветит установку, и неподвижная теневая картина волн будет хорошо видна. Для фотографирования лучше воспользоваться прямым солнечным светом.

Рис. 96

Укрепите теперь на молоточке звонка согнутую из проволоки вилку с кусочками пробки на концах. Расстояние между концами вилки 2-3 см. Если концы будут опускаться в воду одновременно, получится два источника волн, колеблющихся не только синхронно, т. е. в такт, но и синфазно, т. е. волны от обоих источников будут возникать в один и тот же момент времени. Картина будет примерно такой, как на рис. 96 (здесь 2d/λ = 4). От источников волн веером расходятся области больших амплитуд, разделенные областями "молчания". Центральная область больших амплитуд расположена перпендикулярно линии, соединяющей источники. Как области молчания, так и области больших амплитуд проходят между источниками.

Исследование интерференционной картины с линейкой покажет, что расстояние между двумя максимумами на линии, соединяющей источники, равно половине расстояния между двумя горбами, т. е. половине длины волны. Если изменить расстояние между источниками, то изменится и число полос большой амплитуды. На рис. 97 отношение 2d/λ = 2. Чем больше расстояние между источниками, тем больше "перьев" в нашем веере. Но расстояние между максимумами на линии, соединяющей источники, всегда равно половине длины волны. Поэтому общее число полос с максимальной амплитудой будет вдвое больше, чем число длин волн, укладывающееся на расстоянии между источниками. Отсюда следует, что если расстояние между источниками меньше половины длины волны, то интерференции вообще не будет. Такие источники действуют как один, давая одну систему круговых волн. Это можно увидеть, постепенно уменьшая расстояние между источниками. Обратите внимание еще и на то, что, продолжая в какой-нибудь области больших амплитуд фронт волны, проходящий через горб, мы в соседней области встретим впадину. Другими словами: при переходе через нулевую область фаза волны меняется на половину полного колебания.

Рис. 97

Теперь представьте себе, что у нас не два молоточка, а два источника света, излучающих световые волны, и перпендикулярно поверхности воды мы помещаем экран. Мы увидим освещенные места, соответствующие пересечению экрана и областей с большой амплитудой, и темные, не освещенные места. Мы увидим темные и светлые интерференционные полосы. Попробуем объяснить то, что мы сейчас видели.

Нарисуем на листе бумаги обе системы волн так, словно они замерли в какой-то момент (рис. 98). Горбы волн покажем тонкими сплошными линиями, а впадины - пунктирными. Перенумеруем волны, отметив одинаковыми числами те, которые вышли из источников одновременно. Из чертежа видно, что на линию, равноудаленную от источников, одновременно приходят волны, имеющие одинаковые номера. Это и понятно, так как до точек этой прямой волны прошли одинаковые пути. По принципу суперпозиции мы можем заключить, что на этой линии удвоятся как высоты горбов, так и глубины впадин. Результирующие волны отметим толстыми линиями: горбы - сплошными, а впадины - пунктирными. Правее и левее линии 00 лежат точки, в которых горбы одной системы волн совпадут со впадинами другой. В то время как волны от одного источника вызовут в этих точках отклонение вверх, волны от другого в тот же момент вызовут в этих точках отклонение вниз. Суммарное отклонение в этих точках будет близко к нулю. Соединим все такие точки непрерывной линией. Если проследить за нумерацией горбов и впадин, легко заключить, что до всех точек правой линии левые волны проходят путь на половину длины волны больший, чем правые. Для левой линии на половину длины волны отстают правые волны.

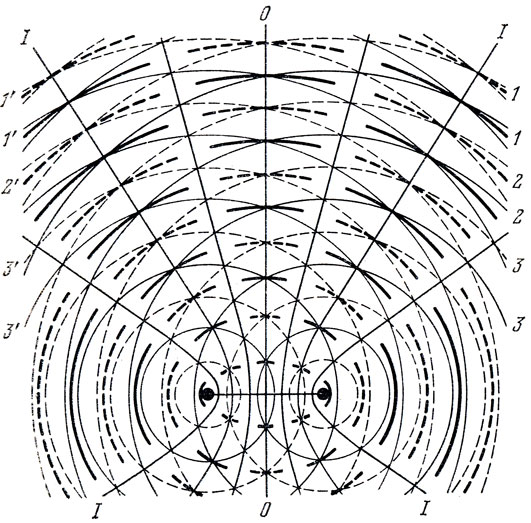
Рис. 98

Справа и слева от нулевых линий лежат точки пересечения первого горба со вторым, второго с третьим и т. д. Легко понять, что это тоже области максимумов. Соединив эти точки, мы получим линию, до точек которой одна система волн отстает от другой на одну длину волны.

Продолжая анализ чертежа, можно найти все нулевые линии и все линии максимумов. Линии, которые мы получили, оказываются гиперболами.

Теперь совершенно ясно, почему расстояние между максимумами на линии, соединяющей источники, равно половине длины волны. Действительно, в среднюю точку этой линии волны приходят в одинаковой фазе и усиливают друг друга. Если сместиться из этой точки на полдлины волны, то путь одной волны увеличится на половину длины волны, а другой - уменьшится на такую же величину. Разность хода между волнами в этой точке (разность путей, пройденных волнами от источников до точки) будет равна одной длине волны, и волны снова будут взаимно усиливаться и т. д. через каждую половину длины волны.

Максимум, соответствующий нулевой разности хода, называют нулевым максимумом или нулевым порядком интерференции. Максимумы с разностью хода в одну длину волны - максимумами первого порядка интерференции и т. д. Максимальный порядок интерференции определяется целым числом, ближайшим к 2d/λ, где d - расстояние между источниками, а λ - длина волны. Теперь попробуйте проанализировать сами с помощью чертежа, а может быть и проверить экспериментально, как изменится картина, если один из источников будет излучать волны с запозданием на половину периода или на какую-нибудь другую его часть. А если сдвиг между колебаниями будет меняться случайным образом? Для экспериментального осуществления волн со сдвигом фаз достаточно сделать концы вилки разной длины.