Волны вероятности

В простейшей модели атома - модели Резерфорда - электроны кружатся по орбитам вокруг ядра подобно тому, как планеты движутся вокруг Солнца. Но электроны - заряженные частицы, и при их вращении обязательно создаются переменные электрические и магнитные поля - возникает излучение, приводящее к потере энергии. Вот почему в планетарной модели электроны ждет незавидная судьба - они обязательно упадут на ядра, и атом разрушится. Но ведь стабильность атомов - это твердо установленный экспериментальный факт.

Нужно было "подправить" модель Резерфорда, и сделал это Нильс Бор в 1913 г. Электронам в модели Бора разрешается вращаться только по определенным орбитам, где они обладают строго заданными энергиями. Изменять эту энергию электроны могут только скачком, излучая и поглощая кванты при переходе с одной орбиты на другую. Такое "квантовое" поведение электронов в атоме позволяет объяснить многое - в частности, устойчивость атома и атомные спектры. Эту модель порой и сейчас используют для упрощенного объяснения квантовых явлений. Но она противоречит соотношению неопределенностей! Ведь при движении даже по квантовой орбите импульс и координата могут быть определены одновременно, а в микромире, как мы теперь знаем, такого быть не может.

Пришлось исправить и эту, как ее называют, квазиклассическую модель атома. Действительная картина, описывающая поведение электрона в атоме, оказалась еще более сложной.

Представьте себе, что нам удалось определить положение электрона в атоме в какой-то момент времени. Сможем ли мы точно сказать, где он будет в следующий момент (для определенности, скажем, через одну секунду)? Нет, измерение координаты, как мы знаем, всегда вносит неопределенность в импульс электрона, и, пользуясь даже самыми лучшими устройствами, нельзя точно предсказать, куда попадет электрон. Что же нам остается в таком случае делать?

Давайте отметим точкой то место в пространстве, где мы обнаружили электрон. Результат еще одного измерения координат электрона в точно таком же атоме снова изобразим точкой в пространстве. Еще измерение - опять точка и т. д. Оказывается, что, хотя и нельзя сказать заранее, где точно будет находиться следующая точка, в характере расположения точек в пространстве имеется определенная закономерность. В некоторых областях точки располагаются гуще, в других - реже, указывая на то, где с большей, а где с меньшей вероятностью может встретиться электрон.

Нам пришлось отказаться от точного описания движения электрона, но мы в состоянии предсказывать шансы обнаружить его в различных точках пространства. Поведение электрона в микромире описывается вероятностно! Такая картина поведения частиц в микромире читателю может не понравиться - уж больно она непривычна, уж больно противоречит нашей интуиции, нашему опыту. Но ничего не поделаешь - так устроена природа. В микромире действуют совсем другие законы, нежели те, к которым мы привыкли в обычной жизни. По образному выражению А. Эйнштейна, приходится "играть в кости" для того, чтобы предсказывать поведение электронов. Без этого, увы, обойтись нельзя^*.

^* (Следует отметить, что сам А. Эйнштейн в необходимость такой "игры" не верил. До конца своей жизни он так и не принял квантовую теорию.)

Итак, в микромире состояние электрона определяется заданием вероятности его обнаружения в разных точках пространства. В нашей наглядной модели мерой вероятности будет плотность меток, и можно представить себе, что эти метки образуют некоторое подобие облака, определяющего образ жизни электрона.

Как устроены облака вероятности? Аналогично тому, как в классической механике законы Ньютона определяют движение тел, в квантовой механике имеется свое уравнение, из которого можно найти "размазку" электрона в пространстве. Такое уравнение придумал в 1925 г. австрийский физик Эрвин Шредингер (заметьте, это случилось раньше, чем было открыто соотношение неопределенностей, то есть раньше, чем прояснилась причина размазки микрочастиц,- такое в физике бывает). Уравнение Шредингера количественно, точно и подробно описывает атомные явления. Но рассказать об этом без сложной математики нельзя. Мы приведем здесь просто ответы - покажем точные портреты размазки электрона в некоторых случаях.

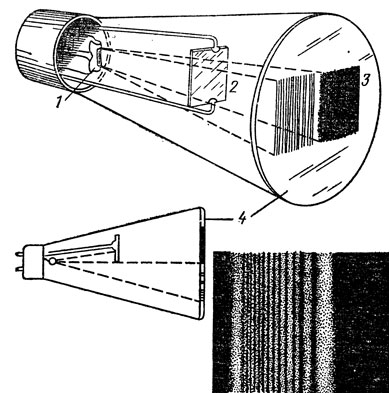
Рис. 2. Такая картина возникает в опыте по дифракции электронов: 1 - электронная пушка; 2 - препятствие; 3 - область тени; 4 - флуоресцентный экран

На рис. 2 показана схема опыта по дифракции электронов и фотография системы полос, возникающей на экране. Картина совершенно аналогична той, которая возникает при дифракции света. Если считать, что электроны движутся по прямолинейным траекториям, как им положено в данном случае по законам классической физики, объяснить этот опыт нельзя. А вот если они размазаны в пространстве, то результат опыта можно понять. Более того, из опыта следует, что облако вероятности обладает волновыми свойствами. С волнами вероятности мы встречаемся и в обычной жизни - например, волны эпидемии, рождаемости, преступности и т. п. В том месте, где амплитуда волны максимальна,- наибольшая вероятность чему-то произойти.

В нашем случае в этих местах с наибольшей вероятностью можно обнаружить электрон, и такие области на фотографии получаются более светлыми.

Рис. 3. Это, конечно, не фотографии реальных электронов, а результаты расчетов, показывающих, как 'размазаны' электроны в атоме. Симметрия этих картинок во многом определяет симметрию молекул и кристаллов. Можно даже сказать, что здесь находится ключ к пониманию красоты упорядоченных форм живой природы

На рис. 3 представлена размазка электрона в различных состояниях атома водорода, найденная на основе точных математических расчетов. Это аналог квантовых орбит, по которым движется электрон в модели атома Бора. Чем светлее область, тем вероятнее встретить в ней электрон. Рисунки напоминают картины стоячих волн, возникающих, когда волновой процесс происходит в ограниченной области пространства. Какие удивительные формы могут принимать облака вероятности! И эти красивые абстрактные картинки действительно определяют поведение электронов в атоме и объясняют, например, уровни энергии и все, что касается химической связи.

Не вдаваясь в детали устройства облаков вероятности, можно с помощью соотношения неопределенностей оценить их характерный размер. Если облако вероятности имеет размер порядка Δх, то бессмысленно говорить о большей, чем Δх, неопределенности в координате частицы. Следовательно, неопределенность импульса частицы Δр_х не может быть меньшей, чем ћ/Δх. По порядку величины это же выражение определяет и минимальное значение импульса частицы.

Чем меньше размер облака вероятности, тем большим становится импульс, и, следовательно, тем быстрее движется частица внутри области локализации. Оказывается, что уже этих общих рассуждений достаточно, чтобы правильно оценить размер атома.

Электрон в атоме обладает кинетической и потенциальной энергиями. Кинетическая энергия электрона - это энергия его движения. Она связана с импульсом по известной формуле E_к = ^mv2/₂ = ^p2/_2m. Потенциальная энергия электрона - это энергия кулоновского взаимодействия с ядром. Для нее также имеется формула: Е_п = -k ^e2/_r, где знак "минус" соответствует притяжению, е - заряд электрона, r - расстояние от электрона до ядра, k - коэффициент, зависящий от выбора единиц измерения.

В каждом состоянии у электрона имеется определенное значение полной энергии Е. Состояние с минимальной энергией называется основным (невозбужденным) состоянием. Оценим размер атома в основном состоянии.

Пусть электрон размазан в некоторой области размером r₀. Притяжение электрона к ядру стремится уменьшить r₀, "схлопнуть" облако вероятности. Этому соответствует уменьшение потенциальной энергии электрона, которая по порядку величины равна -k^e2/_r0 (при уменьшении r₀ растет модуль отрицательной величины). Если бы электрон не обладал кинетической энергией, то он упал бы на ядро. Но, как вы уже знаете, кинетическая энергия у локализованной частицы всегда имеется вследствие соотношения неопределенностей. Оно и "мешает" электрону упасть на ядро! При уменьшении r₀ увеличивается минимальный импульс частицы p₀~ћ/r₀, а следовательно, растет кинетическая энергия Е_к∼ћ²/2mr₀². Из условия равенства нулю производной от полной энергии частицы получаем, что ее минимуму соответствует значение

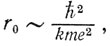
которое определяет характерный размер области локализации электрона в основном состоянии, то есть размер атома. Величина r₀ (r₀~ћ²/kme²) равна 0,05 нм, а мы знаем, что таковы по порядку величины размеры атомов в действительности. Ясно, что соотношение неопределенностей, позволяющее правильно оценить размер атомов,- один из самых глубоких законов микромира.

Для сложных атомов существует определенная закономерность, также непосредственно вытекающая из соотношения неопределенностей. Экспериментально довольно точно определяется работа, которую надо совершить, чтобы вырвать электрон из атома (она равна энергии ионизации Е_и). Так вот, для самых разных атомов произведение √Е_и на размер атома d с точностью до 10-20 % одинаково. Читатель, наверное, догадался, в чем тут дело: импульс электрона р~√2mЕ_и, а постоянство произведения pd следует из соотношения неопределенностей.