3. Книги Вторая, Третья, Четвертая

Книга Первая, как мы уже говорили, содержит весьма подробное изложение гелиоцентрической системы мира. Конечно, Коперник не имел прямых доказательств истинности гелиоцентрического взгляда на Вселенную, однако он обосновал и разработал свое учение настолько, насколько позволили это сделать астрономия, математика, физика и астрономическое приборостроение того времени.

Коперник, отдавая дань великим древнегреческим предшественникам, Платону и Аристотелю, которые считали, что все небесные светила должны равномерно двигаться по самым совершенным, круговым орбитам, также последовал античной традиции и обосновал новую картину мироздания, опираясь на геометрию равномерных круговых движений.

Но не только в этом Коперник следовал античным представлениям. Так же, как и древние астрономы, Коперник считал, что сфера звезд неподвижна. Однако он допускал, что расстояние от Земли до нее практически бесконечно^*.

^* (Задолго до Коперника идею бесконечности Вселенной отстаивал известный философ и ученый Николай Кузапскнй (1401-1464).)

Прежде чем изложить содержание остальной части сочинения Коперника, ознакомимся с основными геометрическими понятиями и моделями, использовавшимися в астрономии на протяжении двух тысячелетий, начиная с эпохи Платона и Аристотеля и вплоть до эпохи Кеплера. Постулат Платона и Аристотеля об идеальности небесных движений никем, в том числе и Коперником, не подвергался никаким сомнениям и служил отправной точкой при построении кинематики Солнечной системы. Но древние астрономы прекрасно знали, что наблюдаемые движения Луны, Солнца и планет относительно звезд неравномерны, поэтому они считали, что их наблюдаемые неравномерные движения суть результат сложения нескольких равномерных круговых движений. Такой же точки зрения придерживался и Коперник, и мы увидим, что в некоторых деталях, касающихся точности расчета планетных движений, он был дальше от истины, чем Птолемей. Прекрасный очерк об эволюции теории планетных движений с древних времен и до эпохи Кеплера содержится в "Этюдах по истории планетных теорий" профессора Н. И. Идельсона, включенных в сборник "Николай Коперник", вышедший в 1947 году в Издательстве АН СССР. Дальше мы не один раз будем пользоваться материалами из этого очерка.

В основу древнейших, доптолемеевских теорий планетных движений (заметим, что Солнце и Луна также считались планетами) были положены геометрические понятия деферента, эпицикла и экс-центра.

Пусть задан параллелограмм TOPN, стороны которого последовательно связаны шарнирами, позволяющими каждой из них вращаться вокруг смежной с ней, и пусть одна из сторон, например сторона параллелограмма ТО, закреплена неподвижно в плоскости, в которой происходит равномерное вращение параллелограмма против часовой стрелки (рис. 14).

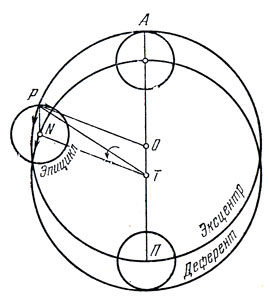
Рис. 14. Изображение деферента, эпицикла и эксцентра

Очевидно, что при этом движение точки N является равномерным вращением по окружности с центром Т и с радиусом TN. Окружность с центром в точке T и с радиусом TN называется деферентом. Так как сторона ТО неподвижна, a NP всегда параллельна ей, отсюда следует, что сторона NP перемещается в плоскости параллельно самой себе и, следовательно, она совершает в плоскости поступательное движение. Но относительно стороны TN отрезок NP совершает вращение по часовой стрелке и точка Р описывает равномерное круговое вращение вокруг точки N по окружности радиуса NP, называемой эпициклом. Нетрудно догадаться, что угловая скорость движения точки N по деференту вокруг точки Т и угловая скорость движения точки Р по эпициклу вокруг N равны между собой, так как один оборот точки N по деференту совершается за то же время, что и один оборот точки Р по эпициклу.

Окружность, которую в равномерном движении описывает точка Р вокруг неподвижного центра О, называется эксцентрическим, кругом (относительно центра Т) или эксцентром. Отношение сторон параллелограмма (или, что то же самое, отношение радиуса эпицикла к радиусу деферента)

называется эксцентриситетом эксцентра.

Радиусы эксцентра и деферента, естественно, равны между собой.

В теории движения планет приведенная кинематическая модель применяется следующим образом.

Если точка Р представляет некоторую реальную планету, равномерно вращающуюся по эпициклу вокруг средней, "фиктивной" планеты N, а наблюдатель находится в точке Т (как говорили древние астрономы, в "центре мира"), то относительно него планета Р будет двигаться неравномерно, в точке П (в перигее) она будет ближе всего к наблюдателю, а в точке А (в апогее) она будет дальше всего от наблюдателя.

Использование этих кинематических понятий древними астрономами значительно облегчалось благодаря изящной теореме Аполлония Пергского, жившего в III веке до нашей эры: кинематическая модель эпицикла и деферента с равными и противоположно направленными вращениями эквивалентна неподвижному эксцентру.

Эту теорему можно, следуя Аполлонию, сформулировать так: если средняя планета N обращается вокруг центра мира Т по деференту в прямом направлении с постоянной угловой скоростью, а реальная планета Р обращается по эпициклу с той же угловой скоростью, но в обратном направлении, то при этих условиях движение планеты Р будет такое же, как если бы она обращалась с той же скоростью в прямом направлении по эксцентру, радиус которого равен радиусу деферента, а центр эксцентра О удален от центра мира на отрезок ОТ, равный и параллельный радиусу эпицикла NP.

При соответствующем подборе отношения радиусов деферента и эпицикла древним астрономам удалось свести неравномерное вращение отрезка (радиуса-вектора) ТР (это единственное наблюдаемое движение) к равномерным вращениям. При этом следует сказать, что в этой кинематической схеме никакой роли не играют сами расстояния TN и NP, а ишь их отношение, т. е. эксцентриситет эксцентра ε.

Это один из существенных пороков геоцентрической системы мира, так как такой подход к описанию движений небесных светил не стимулировал определение реальных расстояний между телами солнечной системы и, следовательно, ее реальных размеров.

И тем не менее построенные античными астрономами описательные, чисто кинематические теории движения видимых невооруженным глазом и посему известных с древних времен пяти планет Меркурия, Венеры, Марса, Юпитера, Сатурна, к которым добавлялись Луна и Солнце, оказались достаточно очными для предсказания положений этих небесных светил на протяжении многих веков. Это интересное обстоятельство обусловлено прежде всего двумя характерными особенностями планетных движений:

1. Плоскости орбит перечисленных выше планет Луны почти совпадают с плоскостью воображаемой траектории движения Солнца вокруг Земли (иначе - с плоскостью земной орбиты вокруг Солнца), называемой плоскостью эклиптики.

Самый большой наклон^* к плоскости эклиптики имеет орбита Меркурия; он равен 7°. Другие планетные орбиты (для известных в то время планет) имеют значительно меньшие наклоны: у Венеры i = 3° 24', у Марса i = 1°51/, у Юпитера i = 1° 18', у Сатурна i = 2° 30'. Лунная орбита наклонена к плоскости эклиптики под углом 5°9'.

^* (Наклон - это двугранный угол между плоскостями орбит двух небесных тел. В астрономии чаще всего обозначается буквой i.)

Малые наклоны планетных орбит обуславливают малые изменения широт планет, и древним астрономам нужно было в основном объяснять изменения со временем только одной из координат - долготы планеты^*.

^* (Широта и долгота - две сферические координаты, определяющие положение светила на небесной сфере. Они аналогичны географической широте и географической долготе. Отличие состоит в том, что за основную координатную плоскость принята плоскость эклиптики (а не плоскость экватора).)

2. Согласно законам планетных движений, открытым позднее Кеплером, каждая планета движется по эллиптической орбите, в одном из фокусов которой находится Солнце. Как оказалось, сплюснутость эллиптических орбит невелика, и по этой причине даже в быстро изменяющейся координате (в долготе) замена истинных эллиптических планетных орбит движением по эксцентру приводит к очень малым ошибкам (они, однако, не ускользнули от проницательного ума Кеплера). Движение по эллипсу не является равномерным, т. е. за одно и то же время радиус-вектор планеты Р (переменное расстояние от Солнца до планеты Р) описывает разные углы с вершиной в Солнце S, однако площади эллиптических секторов равны между собой (рис. 15):

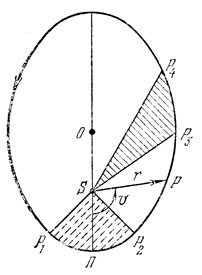
Рис. 15. Эллиптическое движение планеты Р вокруг Солнца S, находящегося в фокусе эллипса

Сплюснутость эллипса характеризуется его эксцентриситетом, который равен отношению расстояния SO от центра эллипса О до фокуса 5 к большой полуоси эллипса а = ОП, т. е.

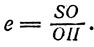
Для планетных орбит эта величина мала, близка к нулю.

Зависимость между радиусом-вектором планеты r и ее истинной аномалией и дается формулой, справедливость которой доказывается в аналитической геометрии^*:

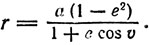
(1)

^* (Истинной аномалией v называется полярный угол текущей точки эллипса, отсчитываемый от большой оси эллипса (для планет -от направления на перигелий орбиты).)

Положение планеты в плоскости орбиты в любой момент времени t полностью определяется координатами r и v, для чего достаточно знать истинную аномалию v в этот момент t, так как по написанной формуле легко можно вычислить r.

Из теории эллиптического движения, полностью разработанной уже после Кеплера и Ньютона, следует, что явная зависимость истинной аномалии v от времени t выражается бесконечным тригонометрическим рядом, коэффициенты которого зависят от эксцентриситета e планетной орбиты. Если отбросить в этом разложении все слагаемые, содержащие третьи и более высокие степени эксцентриситета (e³, e⁴ и т. д.), то для v получим приближенную формулу

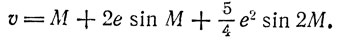
(2)

Величина М называется средней аномалией^* планеты и вычисляется по формуле

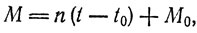
(3)

^* (Средняя аномалия представляет собой угол поворота радиуса-вектора планеты, вычисленный в предположении, что планета равномерно движется по окружности с центром в притягивающем теле, радиус которой равен большой полуоси эллиптической орбиты планеты (при неизменном периоде обращения).)

в которой М₀ - это значение средней аномалии в момент времени t₀, принятый за начальный, n - средняя угловая скорость поворота радиуса-вектора планеты (в небесной механике n называют средним суточным движением), получаемая из соотношения

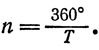
Здесь Т - период обращения планеты вокруг Солнца, выраженный в сутках. Разность

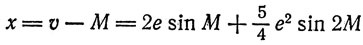
называется уравнением центра. Из последней формулы видно, что в случае круговой орбиты планеты (эксцентриситет e = 0) x = 0 и истинная аномалия v совпадает со средней аномалией планеты М. Уравнение центра характеризует степень неравномерности движения по эллипсу по сравнению с равномерным круговым движением.

Если воспользоваться уравнением центра, то из (1) и (4) в результате математических преобразований можно получить явную зависимость радиуса-вектора планеты г от средней аномалии М (или, что то же самое, от времени t). С принятой выше точностью будем иметь

Таковы современные формулы, определяющие невозмущенное кеплеровское движение.

Что же дает теория эпицикла и деферента или эквивалентная ей теория эксцентра древних?

Если наблюдатель находится в центре эксцентра О, то относительно него планета Р будет двигаться равномерно по эксцентру, следовательно, ее угловая скорость будет постоянной,а угол ПОР будет представлять собой линейную функцию времени. Другими словами, ∠ПОР есть средняя аномалия для теории эксцентра. Можно показать, что она почти не отличается от средней аномалии эллиптического движения, и для наших рассуждений можно предположить, что они совпадают (поэтому мы сохраняем для этой средней аномалии то же самое обозначение М). Угол ПSP = v будет играть роль истинной аномалии планеты Р. Из рис. 16 видно, что величина х, входящая в уравнение центра, представляет угол OPS.

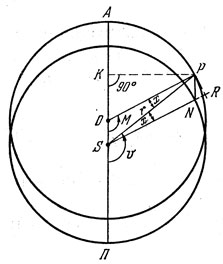
Рис. 16. Изображение основных углов в долготной теории планет

Итак, найдем теперь выражения для r и v, исходя из модели эксцентра, и сопоставим их с кеплеровскими значениями для r и и, полученными выше. Это позволит нам оценить точность теорий Птолемея и Коперника.

Заметим, что древние астрономы и Коперник не пользовались тригонометрическими соотношениями, записанными в виде формул, а давали им словесные описания, но мы здесь ради удобства будем использовать принятую в тригонометрии символику.

Из прямоугольных треугольников ΔKPS, ΔКРО, ΔPRN и ΔPRS имеем соотношения:

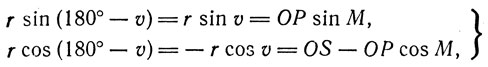
(6)

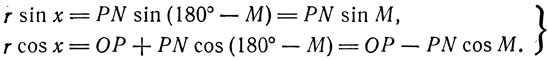
(7)

Из первых двух равенств легко получаем, что

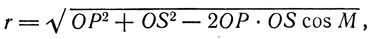
или

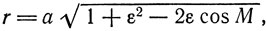
(8)

где а - радиус эксцентра, ε - его эксцентриситет. Сохраняя в последней формуле величины ε и ε², с помощью обобщенной формулы бинома Ньютона^* найдем

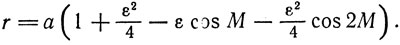
(9)

^* (Справедлива следующая обобщенная формула бинома Ньютона:

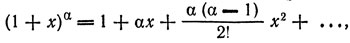
где x мало, а α - любое вещественное число. В данном случае следует положить

)

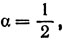
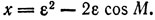
Приведенные формулы дают также соотношение

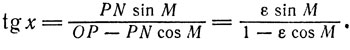
(10)

Пользуясь приближенными формулами

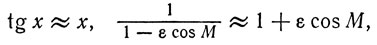
справедливыми для достаточно малых величин x и ε, получим

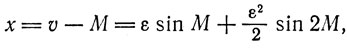
или

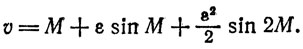
(11)

Формулы (9) и (11) дают соответственно радиус-вектор и уравнение центра планеты с точностью до квадрата эксцентриситета эксцентра.

Полагая теперь эксцентриситет эксцентра равным удвоенному эксцентриситету эллипса (ε = 2e), для модели эксцентра находим

Сравнивая теперь формулы для истинной аномалии эллиптического кеплеровского движения (2) и теории эксцентра (12), получим, что ошибка δv в истинной аномалии (или ошибка в долготе δl)^*, выраженная в радианах, равна ±0,75 e²sin 2M и по модулю не превосходит δl_max = 0,75 e².

^* (Долгота планеты l отличается от ее истинной аномалии на некоторый постоянный угол, поэтому ошибки в l и v всегда одинаковы.)

Один из основоположников древней астрономии, Гиппарх, вычислил эксцентриситет эксцентра Солнца (или Земли) и нашел его равным ε = 0,03348. Эксцентриситет земной эллиптической орбиты на самом деле равен e = 0,016751. Но ε = 2e, и, следовательно, мы имеем прекрасное согласие между этими числами.

Учитывая значение эксцентриситета орбиты Земли, находим, что наибольшая ошибка в долготе Земли, если бы Земля наблюдалась с Солнца, или в долготе Солнца для земного наблюдателя не превышает 43" (это число получается, если δl_max = 0,75 e² преобразовать к градусной мере). Погрешность в долготе значительно меньше погрешности наблюдений древних, и этим объясняется длительное успешное применение теории эксцентра для предсказания видимого положения Солнца относительно звезд. Заметим, что если эксцентриситет орбиты Земли был бы равен эксцентриситету орбиты Марса e = 0,09334, то тогда погрешность в долготе была бы в 30 раз больше (около 21') и несостоятельность теории эксцентра была бы обнаружена намного раньше.

Но для вычисления расстояний теория эксцентра с самого начала оказывается непригодной. Если погрешность в истинной аномалии планеты, обусловленная заменой эллиптической орбиты эксцентром, является величиной, пропорциональной квадрату эксцентриситета, то погрешность в величине радиуса-вектора планеты пропорциональна эксцентриситету. Действительно, сравнивая формулы (5) и (13), получаем, что погрешность

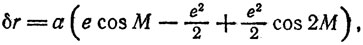
и даже для малых эксцентриситетов величина δr значительна. Но в древних планетных теориях вопросы определения реальных расстояний не затрагивались, и поэтому существенный изъян теории эксцентра остался незамеченным.

Естественно, что большой погрешностью обременены также наименьшее и наибольшее расстояния от наблюдателя до эпицентра (расстояния от центра до перигелия П и до афелия A; см. рис. 16). Согласно теории кеплерова движения, эти расстояния равны

в то время как из теории эксцентра Гиппарха имеем

Птолемей существенным образом улучшил теорию эксцентра, по праву приписываемую Гиппарху, разработав красивый геометрический прием, получивший название "метода биссекции эксцентриситета". Смысл этого метода иллюстрируется на рис. 17. Птолемей предложил считать, что равномерным вращением обладает не радиус эксцентра PC, центр которого, точка С, находится на расстоянии ^аε/₂ от наблюдателя, а прямая ОР или, что то же самое, радиус ОР' окружности, называемой эквантом^*.

^* (Эквант - это круг равномерного движения (буквально - Уравновешивающий круг). Эквантом также называется и центр С - точка выравнивания. Эта точка делит на две равные части отрезок ОТ. Отсюда и название "биссекция эксцентриситета".)

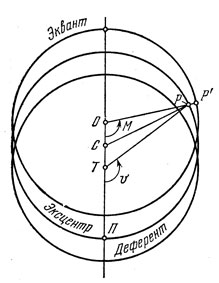
Рис. 17. Изображение кинематической схемы - биссекции эксцентриситета, изобретенной Птолемеем

С помощью тригонометрических соотношений, аналогичных приводившимся выше, для схемы биссекции эксцентриситета можно получить приближенные формулы Птолемея:

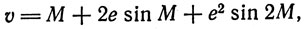
(16)

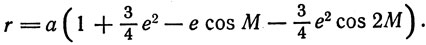
(17)

Сравнивая теперь формулы Птолемея (16) и (17) с формулами Кеплера (2) и (5), видим, что замена эллипса схемой биссекции порождает и в истинной аномалии v и в радиусе-векторе r погрешности, пропорциональные e². В силу этого формулы (16) и (17) при малых эксцентриситетах позволяют весьма точно найти не только долготу планеты l, но и ее радиус-вектор r, если известна величина радиуса деферента а. Эти погрешности равны

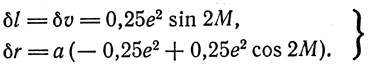
(18)

Гипотеза биссекции эксцентриситета представляет большой шаг вперед, так как в этой схеме движение планет не только кажется неравномерным относительно "центра мира" Г, но и фактически оно неравномерно относительно центра эксцентра. Эта замечательная идея Птолемея о существовании реальных неравномерных вращений не находилась в согласии с принципом идеальности небесных движений Аристотеля и Платона. По-видимому, она оказала немалое влияние на Кеплера, полностью отказавшегося от догмы равномерных круговых движений в своей "Новой астрономии", содержащей два закона планетных движении.

Признавая, что схема биссекции Птолемея более точна для предсказания положений планет, Коперник считал ее несовместимой с постулатами Аристотеля и Платона и поэтому счел необходимым заменить ее другой кинематической моделью, описывающей движения планет практически с той же точностью. Сделав по сравнению с Птолемеем шаг назад в кинематических принципах Солнечной системы, Коперник, однако, дал красивое решение этой задачи, пользуясь схемой двойного шарнирного параллелограмма.

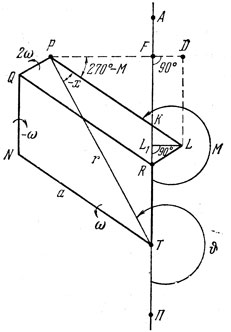
Рис. 18. Кинематическая модель - двойной параллелограмм, предложенная Коперником для объяснения неравномерных движений планет вокруг Солнца

Пусть в двойном параллелограмме TRLPQN (рис. 18 неподвижной является сторона TR, а параллелограммы TRQN и RLPQ вращаются против часовой стрелки, первый с угловой скоростью ω и второй с угловой скоростью 2ω. Введем обозначения:

В своих построениях Коперник полагает

Существуют три эквивалентные кинематические модели движения точки Р относительно "центра мира" Т. Это эпи - эпицикл, эксцентр - эпицикл и эксцентр - эксцентр.

Схема эпи - эпицикла состоит в движении планеты Р против часовой стрелки с угловой скоростью 2ω по эпициклу с радиусом QP = 0,5ae. Его центр Q также описывает эпицикл с радиусом NQ = 1,5ae по часовой стрелке с угловой скоростью ω, а центр последнего эпицикла, точка N, вращается по деференту с радиусом TN против часовой стрелки с угловой скоростью ω. При этом предполагается, что угол TRL во время движения в два раза больше угла PRА.

Схема эксцентр - эпицикла состоит в движении точки Q по эксцентру против часовой стрелки со скоростью со вокруг точки R, а планета Р описывает эпицикл с радиусом QP и с угловой скоростью ω.

Наконец, схема эксцентр - эксцентра заключается в том, что траектория точки L рассматривается как эксцентр относительно "центра мира" T, а орбита планеты Р рассматривается как эксцентр относительно точки R.

Эти кинематические модели и доказательство их эквивалентности характеризуют Николая Коперника как глубочайшего геометра и кинематика своего времени.

Прежде чем говорить о приложении этих кинематических схем к описанию движений планет, сопоставим их с теорией эллиптического кеплерова движения.

На рис. 18 видно, что отрезки PF и TF равны

Из прямоугольных треугольников APFT, APDD и ALLiR получаем тригонометрические соотношения:

Поэтому

После возведения в квадрат и сложения формул (19) и (20) находим, что квадрат радиуса-вектора r планеты Р выражается равенством

Отсюда, пользуясь формулой обобщенного бинома Ньютона и сохраняя члены, пропорциональные e и e², получим

Далее, применяя теорему синусов к ΔPKT, находим

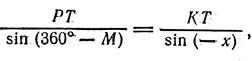
или

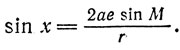
Для малых эксцентриситетов e sin x ≈ x, поэтому с принятой выше точностью из последнего соотношения можно вывести

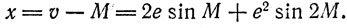
(22)

Погрешности в истинной аномалии и, в долготе l и в радиусе-векторе r планеты Р, обусловленные заменой эллиптической кеплеровой орбиты, схемой эпи - эпицикла Коперника, равны

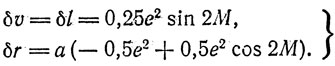
(23)

Сравнивая теперь погрешности схемы биссекции Птолемея (18) и двойного параллелограмма Коперника (23), видим, что погрешности δl в долготе планет с точностью до квадрата эксцентриситета орбиты планеты Р совпадают, в то время как погрешность δr в радиусе-векторе по Копернику в два раза больше, чем у Птолемея. Эти соображения позволяют заключить, что кинематическая модель Коперника по сравнению со схемой биссекции Птолемея менеt удачна для предвычисления положений планет в пространстве, но она объективно явилась источником очень важного замечания, недооцененного самим Коперником. В главе четвертой Книги Пятой утверждается, что орбита планеты Р не может представлять собой в точности окружность не только для наблюдателя, находящегося в точке Т, но и относительно любой точки, находящейся на линии апсид ПА, в том числе и относительно точки R.

В отличие от Птолемея, который в своей теории эквантов молчаливо нарушал принцип идеальности небесных движений и допускал неравномерные круговые движения, Коперник стремился к строгому соблюдению принципа равномерных круговых движений. Поэтому отмеченная не только Птолемеем, но и Коперником невозможность абсолютно точного соблюдения этого принципа представляла собой чрезвычайно плодотворную идею, которая помогла Кеплеру найти истинное направление в поисках законов движения планет.

После этого краткого изложения теории планетных движений мы можем вернуться к содержанию остальной части сочинения Коперника "О вращениях небесных сфер".

Книга Вторая, состоящая из четырнадцати глав, посвящена различным вопросам сферической астрономии: явлениям, связанным с суточным вращением небесной сферы, преобразованию различных систем астрономических координат небесных светил и т. д. Здесь определяются основные круги и точки на небесной сфере (небесный экватор, эклиптика, горизонт, меридиан и пр.), изучаются различные геометрические соотношения между ними, объясняются явления равноденствия и солнцестояния, восхода и захода звезд и многие другие видимые явления, обусловленные как суточным вращением Земли, так и годичным движением Земли по эклиптике.

Заканчивается Книга Вторая каталогом, содержащим долготы и широты (с точностью ±5'), а также видимые звездные величины 1025 звезд.

Книга Третья посвящена детальному изложению разработанной Коперником теории движения Солнца^* и объяснению явления прецессии земной оси. Для описания движения Солнца Коперник использовал кинематическую схему эксцентра (деферента плюс эпицикла), но для того чтобы эта модель хорошо согласовывалась с наблюдениями средневековых астрономов, ему пришлось в схему эксцентра ввести два изменения. По Копернику, центр орбиты Земли не совпадает с центром Солнца, а обращается с периодом в 3434 года вокруг некоторой фиктивной точки, которая в свою очередь делает один оборот вокруг Солнца за 50 000 лет.

^* (Коперник придерживался терминологии, введенной Гиппархом, и говорил о движении Солнца, хотя, конечно, всюду изучаются форма и свойства земной орбиты. Впрочем, и в настоящее время в учебниках по астрономии обсуждается видимое годичное движение Солнца.)

Такая искусственная и громоздкая кинематическая модель, конечно, неприемлема с точки зрения современной динамики, однако она позволила довольно точно определить одну из основных единый времени - длину тропического года^*. Ошибка в продолжительности тропического года у Коперника равна всего 29 секундам.

^* (Тропический год - промежуток времени между двумя последовательными прохождениями Солнца в видимом годичном движении через точку весеннего равноденствия.)

Как мы выше говорили, явление прецессии Коперник объяснял существованием так называемого "деклинационного движения". Хотя применяемые здесь теоретические предпосылки неверны, тем не менее величина годичной прецессии получилась очень близкой (50",20) к действительной ее величине для той эпохи (50", 17).

Содержание Книги Третьей оказалось, пожалуй, дальше других от последующего направления развития астрономии, но при ее чтении поражает тот огромный объем знаний, которым владел великий ученый. Мы здесь также встречаемся с весьма и . весьма большим объемом вычислений, сравнений и сопоставлений, с блеском выполненных Коперником.

Книга Четвертая содержит изложение теории движения Луны, разработанной Коперником. В ней Коперник отказался от кинематической схемы эксцентра и экванта, на которой зиждилась птолемеева теория движения Луны, и построил свою теорию на основе описанной выше схемы эпи - эпицикла

Еще Гиппарху и Птолемею было известно, что истинная аномалия Луны v и ее средняя аномалия М связаны друг с другом более сложным соотношением по сравнению с уравнением центра (16).

Современная теория движения Луны, построенная в прошлом веке американским математиком Георгом Хиллом, дает для истинной долготы^*

^* (Истинная долгота равна сумме двух дуг, лежащих в разных плоскостях:

)

Луны l следующее равенство:

где λ - средняя долгота Луны, D = λ-λ' (разность средних долгот Луны и Солнца), М, М' - средние аномалии Луны и Солнца^*. Формула (24) получена современными математическими методами и учитывает как притяжение Земли, так и притяжение Солнца.

^* (Средние долготы представляют собой долготы, вычисляемые в предположении, что исследуемое тело движется по орбите равномерно с угловой скоростью, равной среднему движению n.)

Если пренебречь возмущающим влиянием Солнца, то в этом случае формула (24) переходит в уравнение центра:

Слагаемые в (25) называются в современной небесной механике эллиптическими членами. Они были найдены еще Гиппархом с помощью модели эксцентра. Пренебрежение влиянием Солнца на движение Луны приводит к значительным ошибкам в долготе, достигающим 80'-100'. Такие ошибки не могли остаться незамеченными древними астрономами. Птолемей первый обратил внимание на эти расхождения в наблюдаемых и вычисленных долготах Луны и существенно обогатил теорию движения Луны, открыв так называемое неравенство эвекции, выражаемое суммой

В своем фундаментальном трактате "Альмагест" Птолемей с помощью модели эксцентра и экванта построил теорию движения Луны, учитывающую эллиптические члены и эвекцию, т. е. для истинной долготы Луны у древних астрономов имелась формула^*

^* (Остальные слагаемые из равенства (24) были найдены значительно позже Коперника.)

Кинематическая схема эпи - эпицикла позволяла Копернику вычислять долготы Луны с той же точностью, что и теория Птолемея, и в этом смысле теории Коперника нельзя отдать какое-то предпочтение по сравнению с теорией Птолемея. Однако он значительно превзошел своего предшественника в определении лунных геоцентрических расстояний для различных положений на лунной орбите. Из теории движения Луны Птолемея следовало, что наибольшее расстояние от Земли до Луны равно 74 земным радиусам (около 470 000 км), а наименьшее расстояние составляет 33 земных радиуса (около 200 000 км). Действительные расстояния Луны от Земли изменяются в пределах от 405 000 км до 356 000 км (с учетом основных возмущающих факторов).

Коперник во второй главе Книги Четвертой очень убедительно критикует недостатки птолемеевой теории. "Больше всего в неправильности этого предположения убеждает нас,- пишет Коперник,- вид диска Луны, который точно так же должен был бы казаться имеющим вдвое больший или вдвое меньший диаметр". Отсутствие подобного явления при наблюдениях Луны и, следовательно, такого значительного изменения расстояния до Луны убедило Коперника в необоснованности применения к Луне модели эксцентра и экванта, и он в третьей главе с названием "Другое мнение о движении Луны" выдвигает свою модель эпи - эпицикла. Далее, в главах IV-XII, с помощью этой модели дается подробнейшее объяснение изменения со временем долготы Луны. Главу XVII Коперник посвящает определению геоцентрического расстояния Луны (выраженного в земных радиусах). Здесь приведено несколько значений лунного расстояния, и среди них имеется, в частности, значение для наибольшего расстояния, равного 64 земным радиусам (около 407 000 км), и значение наименьшего расстояния, равного 52 земным Радиусам (около 332 000 км). Эти результаты намного лучше согласуются с действительными лунными расстояниями, чем птолемеевские определения лунных Расстояний. Коперник достаточно хорошо определил также диаметр Луны в долях земного диаметра (согласно Копернику, диаметр Луны равен 0,2857 земного диаметра, а современные определения дают число 0,2725). Более ошибочны были представления Коперника о величине расстояния от Земли до Солнца.

В главах XXVIII-XXXII Книги Четвертой изложена теория лунных и солнечных затмений. Прежде всего Коперник излагает свой метод вычисления времени соединений и противостояний Луны и Солнца^*, когда происходят солнечные и лунные затмения. В главе XXVIII приведена таблица моментов соединений и противостояний Солнца и Луны на 12 синодических месяцев^** и изменений широты Луны на этот промежуток времени. Если во время эклиптического соединения широта Луны меньше полусуммы угловых диаметров Луны и конуса земной тени, то будет иметь место лунное затмение. В случае солнечного затмения дело обстоит сложнее, так как видимое и истинное соединения этих светил не совпадают. Далее Коперник излагает метод определения продолжительности лунных и солнечных затмений. По сложившейся тогда традиции величина фазы солнечного затмения выражалась в дюймах и она указывала, сколько двенадцатых долей солнечного диаметра покрыто лунным диском. Эти вопросы настолько строго и подробно рассмотрены Коперником, что он, например, замечает, что промежуток времени, в течение которого происходит "затмевание" диаметра Солнца, не равен промежутку времени, в течение которого солнечный диаметр "освобождается" от лунного диска. В конце Коперник излагает метод определения продолжительности затмений не по величине закрытой тенью части диаметра, а по величине закрытой тенью части площади диска.

^* (В момент соединения долготы Солнца и Луны одинаковы, а в момент противостояния разнятся на 180°. Если соединение происходит, когда Луна достаточно близка к плоскости эклиптики, в которой лежит видимый путь Солнца, то происходит солнечное затмение, так как Луна находится между Землей и Солнцем. При противостояниях Луны и Солнца возможны лунные затмения.)

^** (Синодический месяц - это промежуток времени между двумя последовательными одинаковыми фазами Луны. Его средняя продолжительность составляет 29,53 суток.)